Законы сложения и умножения чисел
1) 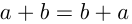 (переместительный закон сложения);
(переместительный закон сложения);
2) 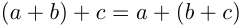 (сочетательный закон сложения);
(сочетательный закон сложения);
3) 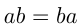 (переместительный закон умножения);
(переместительный закон умножения);
4) 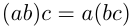 (сочетательный закон умножения);
(сочетательный закон умножения);
5) 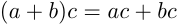 (распределительный закон сложения относительно умножения).
(распределительный закон сложения относительно умножения).
Вернемся к натуральным числам и поговорим о делимости чисел. Разделить натуральное число 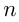 на натуральное число
на натуральное число 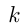 — значит найти такое натуральное число
— значит найти такое натуральное число 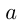 при котором
при котором 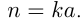 В этом случае говорят, что
В этом случае говорят, что 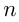 нацело делится на
нацело делится на 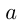 . Число
. Число 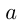 называется делителем числа
называется делителем числа 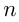 , а число
, а число 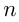 называется кратным числа
называется кратным числа 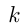 .
.
Натуральные числа бывают простые и составные. Натуральное число называется простым, если оно не имеет делителей, кроме 1 и самого себя. Все остальные натуральные числа, кроме 1, составные. Они могут быть разложены на простые множители, т.е. представлены в виде произведения простых множителей. Например, 5, 7, 13, 29 — простые числа, 6, 18, 33, 45 — составные числа: 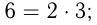
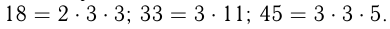
Число 1 не относят ни к простым, ни к составным числам.
Разложение составного числа на простые множители является для него единственно возможным.
Натуральные числа, делящиеся на 2, называются четными, не делящиеся на 2 — нечетными.
Признак делимости на 2: число делится на 2, если его последняя цифра четная или 0.
Признак делимости на 3: число делится на 3, если сумма его цифр делится на 3.
Признак делимости на 4: число делится на 4, если две его последние цифры либо нули, либо образуют число, делящееся на 4.
Признак делимости на 5: число делится на 5, если его последняя цифра либо 0, либо 5.
Признак делимости на 9: число делится на 9, если сумма его цифр делится на 9.
Признак делимости на 10: число делится на 10, если его последняя цифра 0.
Любое четное число 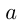 может быть записано как
может быть записано как 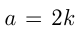 , любое нечетное число
, любое нечетное число 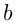 как
как 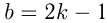 , где
, где 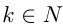 .
.
Если несколько натуральных чисел делятся на одно и то же число, то это число называется их общим делителем. Наибольшее из таких чисел называется наибольшим общим делителем (НОД). Если наибольший общий делитель чисел равен 1, то такие числа называются взаимно простыми. Наименьшим общим кратным (НОК) нескольких натуральных чисел называется наименьшее число, которое делится на каждое из данных чисел.
Для отыскания НОД двух чисел можно сделать следующее:
1) разложить каждое из чисел на простые множители;
2) найти произведение одинаковых простых множителей, входящих и в то, и в другое разложения. Например, даны числа 180 и 120. Найти НОД этих чисел.
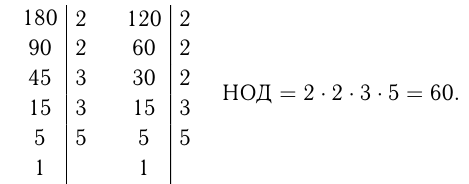
Для нахождения НОК двух чисел можно выполнить следующее:
- разложить каждое из чисел на простые множители;
- найти произведение всех различных простых множителей, входящих в оба разложения.
Например, найти НОК чисел 180 и 140.
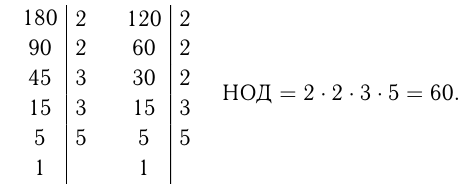
Запись 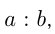 , или
, или 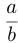 называется отношением числа
называется отношением числа 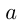 к числу
к числу 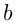 .
.
Равенство двух отношений 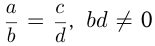 называется про-порцией, а числа
называется про-порцией, а числа 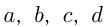 — членами пропорции, при этом числа
— членами пропорции, при этом числа 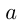 и
и 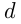 считаются крайними членами пропорции, а числа
считаются крайними членами пропорции, а числа 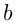 и
и 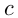 — средними членами пропорции. Основное свойство пропорции:
— средними членами пропорции. Основное свойство пропорции: 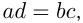 т.е. произведение крайних членов пропорции равно произведению средних ее членов.
т.е. произведение крайних членов пропорции равно произведению средних ее членов.
Если 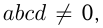 то из пропорции
то из пропорции 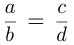 можно получить ещё три пропорции :
можно получить ещё три пропорции : 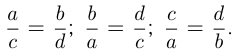 Отношения величин и пропорции часто используются при решении задач. Например, решить уравнение:
Отношения величин и пропорции часто используются при решении задач. Например, решить уравнение:
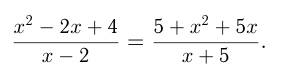
Пользуясь свойством пропорции и учитывая, что 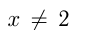 и
и 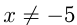 , запишем:
, запишем: 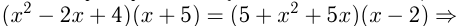
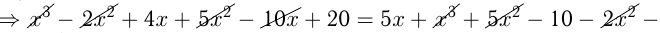
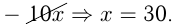
Процентом данного числа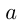 называется его сотая часть. Следовательно, само число составляет сто процентов. Один процент обозначается символом 1%.
называется его сотая часть. Следовательно, само число составляет сто процентов. Один процент обозначается символом 1%.
Например, 45% числа 50 есть 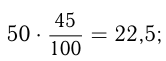 30% числа 200 есть
30% числа 200 есть 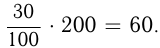 В дальнейшем мы увидим, что проценты, процентные соотношения часто используются при решении задач.
В дальнейшем мы увидим, что проценты, процентные соотношения часто используются при решении задач.
На множестве действительных чисел определено понятие степени.
Степенью 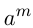 , где
, где 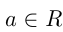 ,
, 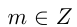 (степень с целым показателем) называется число, определяемое правилами:
(степень с целым показателем) называется число, определяемое правилами:
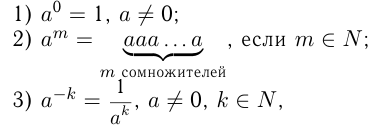
- где
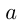 — основание степени;
— основание степени; -
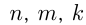 — показатели степени.
— показатели степени.
Понятие степени с рациональным показателем связано с понятием арифметического корня 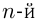 степени из числа
степени из числа 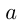 при
при 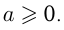 Число
Число 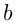 называется арифметическим корнем
называется арифметическим корнем 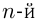 степени из неотрицательного числа
степени из неотрицательного числа 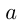 , если
, если 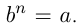 Обозначается
Обозначается 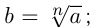
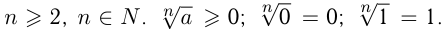 Например,
Например, 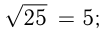
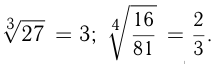
Свойства арифметических корней: при 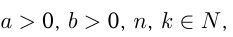
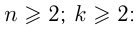
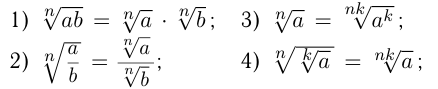
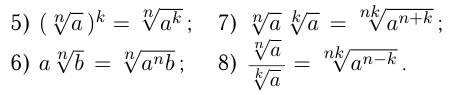
Степенью числа 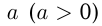 с рациональным показателем
с рациональным показателем 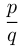 называется арифметический корень степени
называется арифметический корень степени 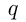 из
из 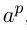 , т.е.
, т.е. 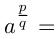
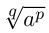 . Если
. Если 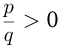 и
и 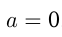 , то
, то 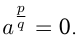 Из определения следует:
Из определения следует: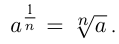 Например,
Например, 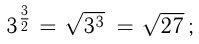
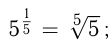
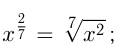
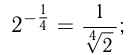
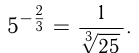
Расширяя понятие степени, можно, исходя из непрерывности функции 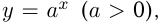 определить степень числа
определить степень числа 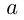 с любым действительным показателем. Таким образом, степень
с любым действительным показателем. Таким образом, степень 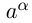 существует при
существует при 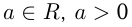 и
и 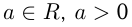 Степени обладают следующими свойствами:
Степени обладают следующими свойствами:
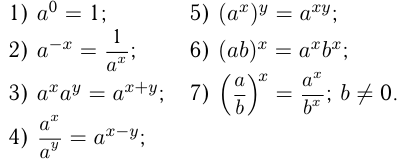
Непосредственным образом с понятием степени связано понятие логарифма.
Если 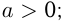
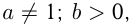 то логарифмом числа
то логарифмом числа 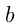 по основанию
по основанию 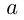 называется показатель степени, в которую нужно возвести число
называется показатель степени, в которую нужно возвести число 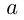 , чтобы получить число
, чтобы получить число 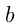 . Запись
. Запись 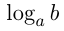 читается: логарифм
читается: логарифм 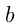 по основанию
по основанию 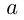 .
.
Если 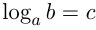 , то
, то 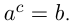 Отсюда следует основное логарифмическое тождество:
Отсюда следует основное логарифмическое тождество: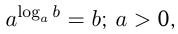
Свойства логарифмов:

Например, т.к. 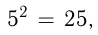 то
то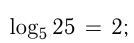 т.к.
т.к. 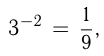 то
то 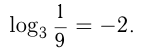
Из основного логарифмического тождества следует, например, что 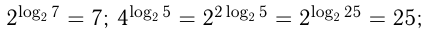
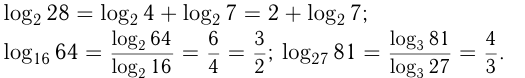
Логарифм по основанию 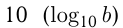 называется десятичным логарифмом и обозначается
называется десятичным логарифмом и обозначается 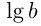 ; логарифм по основанию
; логарифм по основанию 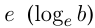 называется натуральным логарифмом и обозначается
называется натуральным логарифмом и обозначается 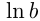 . Операция взятия логарифма числа по определенному основанию называется логарифмированием, обратная операция избавления от логарифма — потенцированием.
. Операция взятия логарифма числа по определенному основанию называется логарифмированием, обратная операция избавления от логарифма — потенцированием.
Итак, повторим: над действительными числами при определенных ограничениях можно производить следующие операции — сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, логарифмирование, потенцирование.
Есть еще одна операция над числами, на которую мало обращают внимание, но которая тем не менее важна и, как мы увидим в дальнейшем, часто используется при решении уравнений и неравенств: это операция взятия числа по модулю.
Абсолютная величина, или модуль, числа 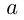 обозначается
обозначается 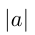 и определяется, как уже говорилось, следующим образом:
и определяется, как уже говорилось, следующим образом:
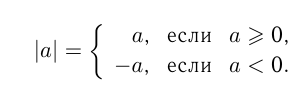
Отсюда следует, что 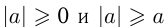 а для всех
а для всех 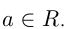 Например,
Например, 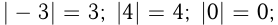
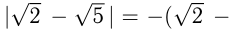
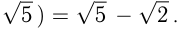
Свойства модуля числа:
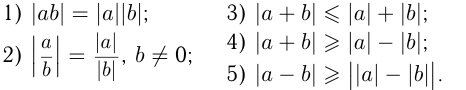
Взятие числа по модулю используется при извлечении корня четной степени. Так, 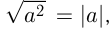 , и в общем случае
, и в общем случае 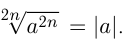 Например,
Например,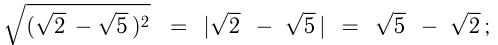
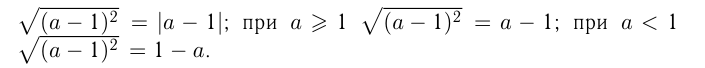
Из чисел, знаков действий и скобок можно составить различные числовые выражения. Преобразование числового выражения обычно имеет своей целью вычисление его значения.
Итак, дробь 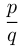 , где
, где 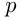 — целое, a
— целое, a 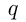 — натуральное число, является рациональным числом и может быть представлена в виде либо конечной, либо бесконечной периодической десятичной дроби. Всякая бесконечная непериодическая десятичная дробь является иррациональным числом. Иррациональное число нельзя представить в виде дроби
— натуральное число, является рациональным числом и может быть представлена в виде либо конечной, либо бесконечной периодической десятичной дроби. Всякая бесконечная непериодическая десятичная дробь является иррациональным числом. Иррациональное число нельзя представить в виде дроби 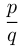 , и обратно, каждое число, не пред-ставимое в виде дроби
, и обратно, каждое число, не пред-ставимое в виде дроби 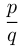 , является иррациональным. Мы знаем иррациональное число
, является иррациональным. Мы знаем иррациональное число 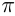 , появляющееся при измерении длины окружности и площади круга; иррациональное число
, появляющееся при измерении длины окружности и площади круга; иррациональное число 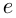 , используемое в теории пределов и являющееся основанием натуральных логарифмов, а также числа, получающиеся при извлечении корней, например,
, используемое в теории пределов и являющееся основанием натуральных логарифмов, а также числа, получающиеся при извлечении корней, например, 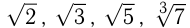 и т. д.
и т. д.
Таким образом, числовые выражения включают все действительные числа: натуральные, целые, рациональные и иррациональные.
Если в выражение входят не только числа, но и буквы, то это выражение называется алгебраическим.
Алгебраическое выражение называется рациональным, если над входящими в него буквами совершаются только действия сложения, вычитания, умножения, деления и возведения в натуральную степень.
Если в алгебраическом выражении над буквами совершается действие извлечения арифметического корня, то выражение называется иррациональным.
Рациональное выражение называется целым относительно некоторой входящей в него переменной величины, если в выражении отсутствует деление на эту переменную или на выражение с этой переменной. В противном случае алгебраическое выражение называется дробно-рациональным относительно этой переменной.
Алгебраическое выражение имеет область определения, т.е. совокупность всех числовых значений переменных, при которых выражение имеет смысл.
Два выражения называются тождественно равными, если при всех значениях входящих в них букв из общей области определения числовые значения выражений равны.
Если на некоторой области определения из справедливости одного равенства следует справедливость второго и, наоборот,
из справедливости второго следует справедливость первого, то такие равенства называются равносильными на этой области. Равносильное преобразование обозначают 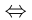
Рациональное алгебраическое выражение, действия над переменными в котором есть только умножение и возведение в степень, называется одночленом. Сумма и разность одночленов называется многочленом. Выражение вида 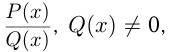 , где
, где  — многочлены, называется рациональной или алгебраической дробью.
— многочлены, называется рациональной или алгебраической дробью.
Например, 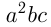 — рациональное алгебраическое выражение, одночлен;
— рациональное алгебраическое выражение, одночлен;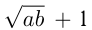 — иррациональное алгебраическое выражение;
— иррациональное алгебраическое выражение; 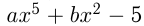 — целое рациональное алгебраическое выражение, многочлен;
— целое рациональное алгебраическое выражение, многочлен; 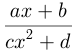 алгебраическая дробь. Стандартным видом одночлена называется произведение, составленное из числового множителя (коэффициента) и степеней различных переменных. Например,
алгебраическая дробь. Стандартным видом одночлена называется произведение, составленное из числового множителя (коэффициента) и степеней различных переменных. Например, 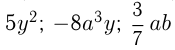 — одночлены стандартного вида.
— одночлены стандартного вида.
Степенью одночлена стандартного вида называется сумма показателей степеней переменных. Например, 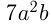 — одночлен 3-й степени;
— одночлен 3-й степени; 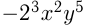 — одночлен 7-й степени.
— одночлен 7-й степени.
Одночлены, отличающиеся только коэффициентами или равные между собой, называются подобными.
В многочлене подобные одночлены, называемые подобными слагаемыми, можно заменить одним одночленом, если сложить их коэффициенты. Такое преобразование называется приведением подобных слагаемых.
Например, 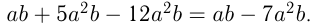 Если в многочлене одночлены записаны в стандартном виде и приведены подобные слагаемые, то многочлен называется многочленом стандартного вида. Степенью многочлена считается наибольшая степень входящего в него одночлена.
Если в многочлене одночлены записаны в стандартном виде и приведены подобные слагаемые, то многочлен называется многочленом стандартного вида. Степенью многочлена считается наибольшая степень входящего в него одночлена.
Сумму или разность многочленов можно преобразовать в многочлен стандартного вида. Для этого нужно раскрыть скобки и привести подобные слагаемые. При раскрытии скобок знаки всех слагаемых в скобках сохраняются, если перед скобкой стоит знак «+», и меняются на противоположные, если перед скобкой стоит знак «—».
При умножении многочлена на одночлен каждый член многочлена умножается на одночлен, и эти произведения складываются. При умножении многочлена на многочлен каждый член 1-го многочлена умножается на каждый член 2-го многочлена, и полученные произведения складываются.
Например, 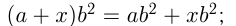
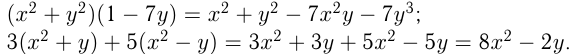
Преобразование многочлена в произведение двух или нескольких многочленов (одночленов) называется разложением многочлена на множители. Для таких преобразований можно использовать способ вынесения общего множителя за скобки, способ группировки, а также формулы сокращенного умножения. Так, если во всех слагаемых многочлена присутствуют одинаковые множители, например, 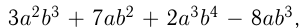 где
где 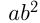 — такой множитель, пишут
— такой множитель, пишут 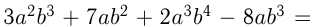
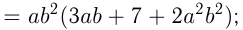
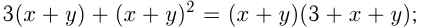
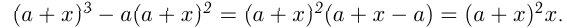
Если все члены многочлена не имеют общего множителя, отличного от 1, можно использовать способ группировки. Для этого надо объединить в группы те члены, которые имеют общий множитель, и вынести его за скобки в каждой группе. Если у всех групп после этого окажется общий множитель, его выносят за скобки.
Например, 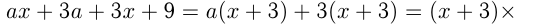
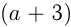

Формулы сокращенного умножения:
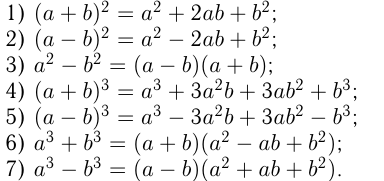
Примеры применения этих формул:
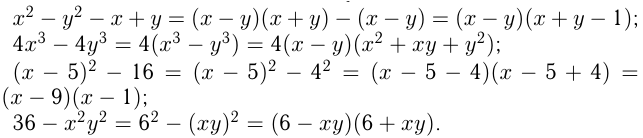
Преобразование алгебраических выражений является одним из основных этапов решения многих математических задач. Умение экономно и правильно производить выкладки при преобразованиях числовых и алгебраических выражений очень важно. В частности, при вычислениях полезно не спешить сразу выполнять арифметические действия, а пытаться сначала упростить выражение. Наибольшего эффекта можно достигнуть с помощью таких преобразований как сокращение дробей, приведение к общему знаменателю, разложение на множители.
Эта теория с решениями взята со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Преобразование числовых выражении с примерами решения |
| Упростить выражение задачи с решением |
| Решение задач на функции по математике |
| Числа, числовые и алгебраические выражения |

