Законы больших чисел и предельные теоремы с примерами решения и образцами выполнения

Важную роль в теории вероятностей и приложениях играют утверждения, устанавливающие характер поведения больших совокупностей случайных величин. Дело в том, что отдельно взятая величина плохо прогнозируема — значения, принимаемые ею в конкретном эксперименте, случайны, и, даже зная ее закон распределения, мы не в состоянии предугадать результат. Замечательным свойством больших совокупностей является то их свойство, что при весьма неограничительных условиях они, в отличие от единичной случайной величины, ведут себя почти детерминировано: с увеличением числа рассматриваемых случайных факторов суммарное воздействие, обусловленное этими факторами, становится все менее случайным.

Важнейшими из утверждений, формализующими подобные, давно подмеченные практиками закономерности, являются законы больших чисел и предельные теоремы. Их обсуждению мы и посвятим настоящую главу.

Законы больших чисел

Пусть 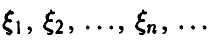— попарно независимые случайные величины, обладающие математическими ожиданиями 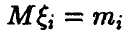, и дисперсиями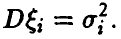

Теорема:

Закон больших чисел в форме Чебышева.

Если дисперсии 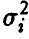равномерно ограничены, т.е.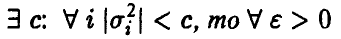

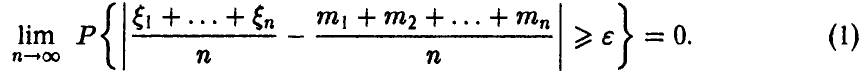
◄ Для доказательства предельного соотношения (1) заметим, что случайная величина 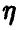, задаваемая соотношением

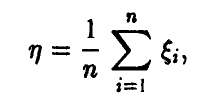
обладает математическим ожиданием 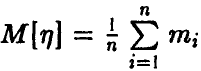дисперсией 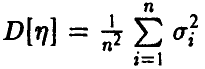и, следовательно, удовлетворяет неравенству Чебышева

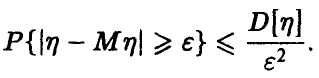
Из условия теоремы следует, что

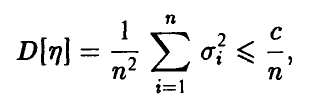
поэтому для любого фиксированного значения 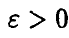имеем

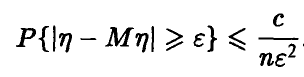
Переходя в последнем соотношении к пределу при 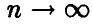, получаем искомое. ►

Доказанная теорема устанавливает, что с ростом количества случайных величин их среднее арифметическое сколь угодно мало отличается от детерминированного, неслучайного воздействия, обусловленного средним арифметическим математических ожиданий.

Было бы неверно понимать соотношение (1) буквально, как утверждение о близости среднего арифметического случайных величин и среднего арифметического их математических ожиданий. Какое бы (может быть, очень маленькое) число є мы ни взяли, в подавляющем большинстве экспериментов разница между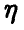 и 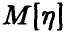будет не больше є, причем доля таких случаев тем больше, чем больше n. В приведенной формулировке закон больших чисел оставляет возможность такого «плохого» эксперимента, когда разница между 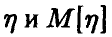будет большой (больше ), однако доля таких, «плохих» экспериментов тем меньше, чем больше n.

В приложениях (особенно в статистической физике) важную роль играет частный случай приведенной выше теоремы, относящийся к одинаково распределенным независимым слагаемым.

Следствие:

Закон больших чисел в форме Чебышева для одинаково распределенных слагаемых.

Пусть — независимые, одинаково распределенные случайные величины с 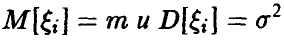Тогда

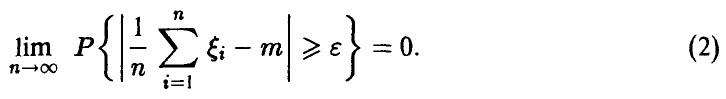
Замечание:

Условие существования дисперсий может быть опущено (закон больших чисел в форме Хинчина).

Другим важным следствием теоремы Чебышева является теорема Я. Бернулли.

Следствие:

Закон больших чисел в форме Бернулли.

Пусть 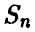— число успехов в серии из n независимых испытаний с постоянной вероятностью успеха р в каждом испытании и 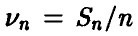— относительная частота числа успехов. Тогда с увеличением количества экспериментов п в подавляющем большинстве случаев частота 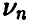будет мало отличаться от вероятности. Точнее

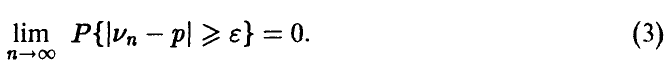
◄ Доказательство следует из (2), если взять 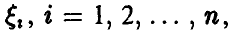такие, что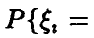 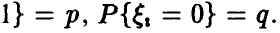Тогда 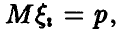дисперсия величины 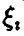существует, равна pq и применима теорема Чебышева, при этом

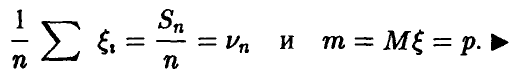
Теорема Чебышева и ее следствия позволяют делать по результатам наблюдений за экспериментом достаточно надежные заключения о поведении случайных величин: дело в том, что относительная частота 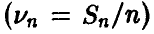события — вещь, определяемая экспериментально, а утверждение (3) связывает ее с вероятностью события и, тем самым, дает путь определения последней по результатам наблюдений.

При использовании законов больших чисел полезно иметь в виду следующее важное обстоятельство: они устанавливают близость относительной частоты 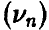и вероятности (р), но они не утверждают, что среднее число успехов (рn) мало отличается от наблюдаемого числа успехов 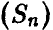! Поясним эту мысль следующим примером.

Пример:

Пусть производится эксперимент с физически симметричной монетой, так что вероятности выпадения герба и решки можно считать одинаковыми, р = q = 1/2.

Можно ли утверждать, ссылаясь на закон больших чисел, что при достаточно длительном экспериментировании число выпавших гербов (Г) и решек (Р) будет примерно одинаковым, т. е.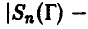

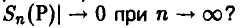
Пусть 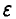— фиксированное положительное число. Закон больших чисел позволяет заключить, что при некотором, может быть, достаточно большом 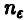выполняется (в подавляющем большинстве случаев) неравенство

Отсюда

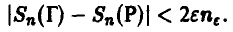
Но, как мы увидим ниже (п. 5.2.1), величина 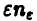ведет себя как 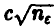, где с — постоянная, и следовательно, в достаточно длинной серии бросаний разность количества выпавших гербов и решек симметричной монеты может стать сколь угодно большой!

Закон больших чисел в этой ситуации позволяет только утверждать, что отношение количеств выпавших гербов и решек близко к единице,

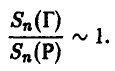
Пример:

Пусть монету бросили 100 раз и 100 раз выпал герб. Какой результат следует ожидать при 101-м испытании?

Теоретически возможны следующие три способа рассуждения в этой ситуации:

1. Монета симметрична, однако случайно так получилось, что выпало 100 гербов подряд. В силу независимости испытаний в 101 раз следует ожидать с равными вероятностями герб или решку.

2. Частота выпадения герба оказалась равной 1. Поэтому (закон больших чисел) монета скорее всего несимметрична и 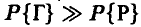. В силу независимости испытаний в 101 раз скорее всего выпадет герб.

3. Монета симметрична, однако случайно так получилось, что выпало 100 гербов подряд. Поскольку закон больших чисел утверждает, что частоты должны быть близки к вероятностям, а вероятность выпадения решки, в силу предположения о симметричности, равна 0,5, то и частота должна быть близка к 0,5. Поэтому чем больше гербов выпало, тем вероятнее, что (для исправления искажения в частоте выпадения решек!) появится решка.

◄ Внимательный анализ закона больших чисел позволяет в рассматриваемой ситуации сделать следующие выводы:
— первое умозаключение теоретически безупречно, однако гипотеза о симметричности малоправдоподобна — чтобы симметричная монета сто раз подряд в независимых испытаниях выпала гербом, необходимо чтобы осуществилось событие с вероятностью 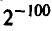. Поэтому скорее всего следует результат объяснить несимметричностью монеты;
— второе умозаключение теоретически безупречно и практически приемлемо;
— третье умозаключение просто неверно, так как неявно предполагает наличие у монеты «памяти» — вероятность выпадения решки связывается с количеством решек, выпавших до рассматриваемого испытания. ►

Завершая обсуждение законов больших чисел, рассмотрим еще один пример, качественно иллюстрирующий логику их применения.

Пример:

Правило среднего арифметического.

Пусть а — некоторая величина, определяемая в эксперименте путем измерений. Каждое измерение 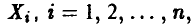складывается из значения а измеряемой величины и погрешности измерения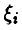

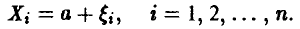
Практиками давно установлено, что для определения измеряемой величины а следует найти среднее арифметическое измерений

◄ Объяснение этому правилу дает закон больших чисел. Если предположить, что систематическая ошибка измерений отсутствует, т. е. 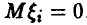, то из соотношения (5) следует

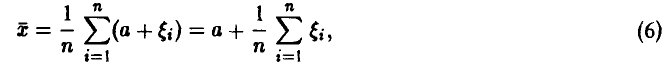
и для последнего слагаемого из закона больших чисел получаем

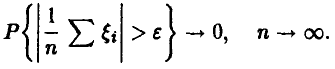
Тем самым, в подавляющем большинстве экспериментов ошибка измерений 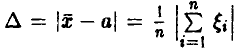может быть неограничено уменьшена за счет дублирования измерений.

Ниже (п. 5.2.2) мы уточним этот качественный результат количественно. ►

Заметим в заключение, что законы больших чисел (в приведенных выше формулировках) утверждают устойчивость средних арифметических больших совокупностей случайных величин, в частности (в формулировке Бернулли), устойчивость частот. Это теоретические утверждения являются следствием постулатов, положенных в основание теории. Очевидно, что в реальной практической ситуации подобная устойчивость не обязана иметь место! Применимость же теории вероятностей к описанию различных явлений в природе и обществе базируется именно на наличии в этих явлениях статистической устойчивости.

Важно понимать, что подобная устойчивость должна быть установлена исследователем (или, по крайней мере, продекларирована) для того, чтобы теоретико-вероятностные выводы имели смысл. Наличие теорем типа законов больших чисел не может служить основанием для утверждений о наличии статистической устойчивости в той или иной конкретной ситуации.

Предельные теоремы

Как следует из результатов предыдущего пункта, среднее арифметическое большой совокупности случайных величин при определенных условиях ведет себя почти детерминировано — мало отличается от среднего арифметического их математических ожиданий. Это утверждение носит качественный характер и в практической ситуации не всегда содержательно. Точный ответ на вопросы «При каких n…?» и «Насколько и как часто отличается совокупное случайное среднее от неслучайного среднего математических ожиданий?» в рамках законов больших чисел (в приведенных формулировках) получить нельзя.

Развитая выше теория (гл. XL, п. 3.2) говорит, что необходимо знание распределения суммы 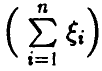или, что то же, средней суммы 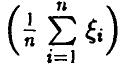. Однако, как уже отмечалось, задача нахождения закона распределения суммы случайных величин в общем случае — это довольно сложная в теоретическом плане и громоздкая в плане технической реализации задача, требующая знания законов распределения слагаемых. Так что для случайных величин, законы распределений которых «плохо» сворачиваются, получение распределений их сумм для достаточно больших значений п задача, скорее всего, практически нереализуемая. Впрочем, и для «хорошо» сворачивающихся распределений работа с распределением суммы большого числа слагаемых может оказаться технически затруднительной.

Спасти ситуацию может только чудо, и таким чудом в теории вероятностей как раз и являются предельные теоремы.

Теорема Муавра—Лапласа

Мы начнем изучение ситуации с довольно простого на первый взгляд, но важного для приложений случая, когда все 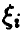— независимые, одинаково распределенные случайные величины, принимающие значения 1 и 0 с вероятностями р и q соответственно, р + q = 1. В этом случае 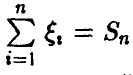— биномиальная случайная величина с параметрами (n, р), распределение которой нам хорошо известно

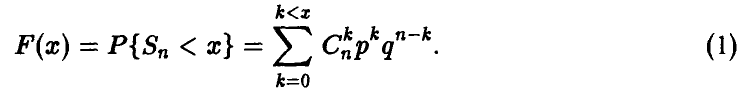
Вероятности, связанные с суммой , в принципе легко могут быть найдены для

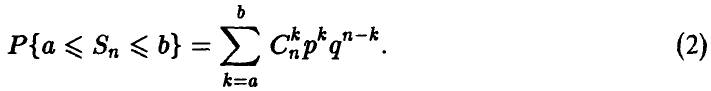
Однако уже для небольших значений п воспользоваться соотношением (2) довольно трудно — вычисления оказываются очень громоздкими.

Пример:

Сколько раз следует подбросить симметричную монету, чтобы с надежностью х, не худшей чем 0,99, частота появления герба отличалась от вероятности не больше, чем на 0,01?

◄ Для получения ответа на вопрос задачи следует решить неравенство

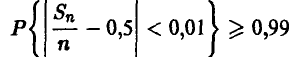
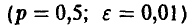относительно n. Использование соотношения (2) приводит к неравенству

для которого проверка, удовлетворяет ли ему, к примеру, число n = 100, — довольно утомительная вычислительная задача. ►

К счастью, для больших значений n может быть указано сравнительно простое правило вычисления вероятностей (1)-(2).

Сначала заметим, что если 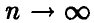, то выражение для индивидуальных вероятностей 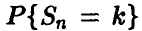может быть упрощено за счет замены факториалов приближенным выражением по известной из анализа формуле Стирлинга

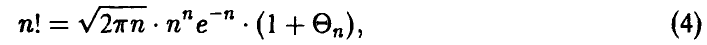
где 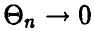при 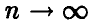. Действительно, легко убедиться в том, что

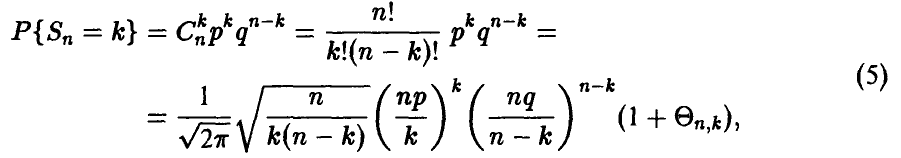
где 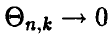при .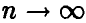

Ниже запись

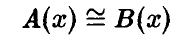
будет обозначать, что 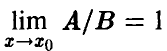или, что то же,

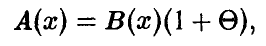
где 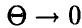при

В силу закона больших чисел, при больших значениях n сумма 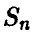с заметной вероятностью принимает только те значения k, которые удовлетворяют условию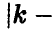 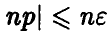Полагая

заключаем, что 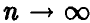влечет за собой 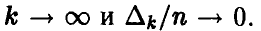Подставим выражения для 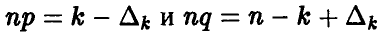в формулу (5) и получим, что

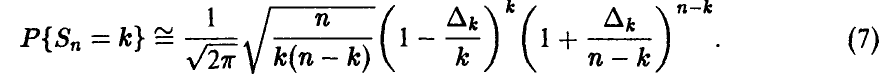
Отсюда

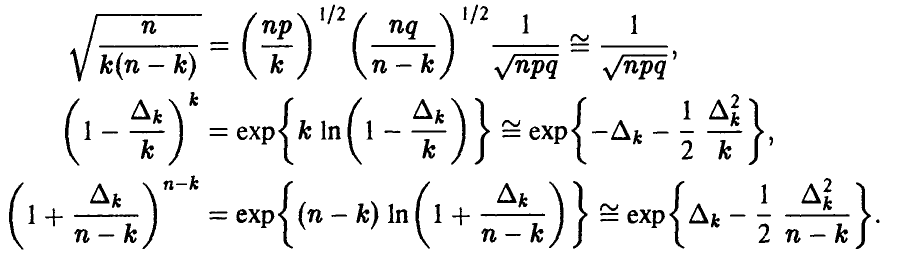
С учетом полученных соотношений равенство (7) примет вид

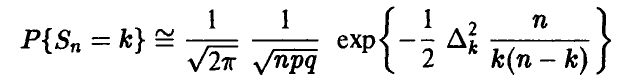
или, после замены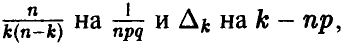

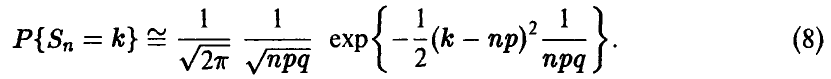
Последнее соотношение представляет собой приближенную формулу для подсчета индивидуальных биномиальных вероятностей и составляет содержание локальном предельной теоремы Муавра— Лапласа. Она пригодна в ситуациях, когда р и q не слишком малы и не слишком близки к единице (в этом случае, как мы знаем, можно использовать приближение Пуассона), а n достаточно велико. Практически же, если nр > 10, 0,1 <р< 0,9 , то вычисление индивидуальных биномиальных вероятностей 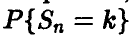по формуле (8) дает вполне приемлемые результаты.

Пример:

Симметричную монету бросили 20 раз. Какова вероятность того, что герб появится ровно 7 раз?

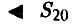— количество появлений герба в рассматриваемом эксперименте, 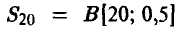Поэтому

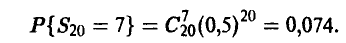
Формула (8) дает: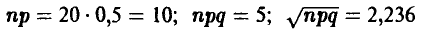

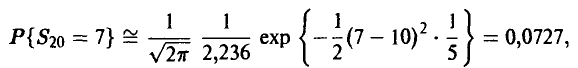
что практически неотличимо от точного результата. ►

Для решения задачи приближенного вычисления совокупных биномиальных вероятностей (1)-(2) рассмотрим соотношение (2) с учетом выражения (8) для индивидуальных биномиальных вероятностей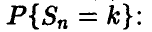

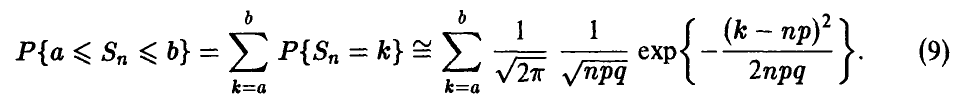
Положим

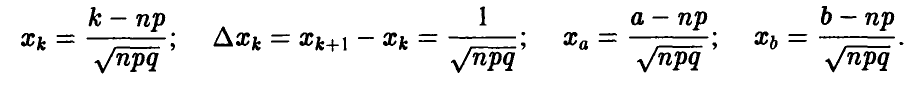
Заметим, что при неограниченном увеличении п промежуток 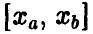изменения переменной х передвигается вдоль числовой прямой неограниченно вправо, при этом его длина 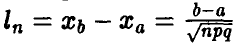неограниченно уменьшается. Поэтому, вообще говоря, нет смысла пытаться вычислять сумму (9) при фиксированных а и b — с увеличением n эта сумма стремится к нулю.

Пусть 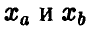фиксированы. Тогда в принятых обозначениях сумма (9) запишется в виде

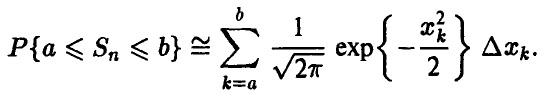
При выражение справа можно интерпретировать как интегральную сумму для интеграла

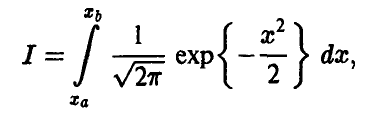
что приводит к следующему утверждению, впервые установленному Муавром для р = q = 1/2 и обобщенному Лапласом на случай произвольных р.

Теорема:

Интегральная теорема Муавра—Лапласа.

Пусть 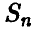— биномиальная случайная величина с параметрами 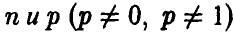. Тогда при 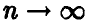равномерно относительно 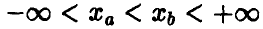справедливо соотношение

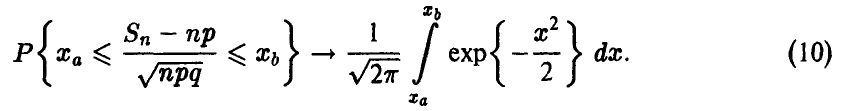
Предельное соотношение (10) является источником формул приближенного вычисления совокупных биномиальных вероятностей.

В самом деле, пусть п достаточно велико, так что (10) имеет место. Тогда

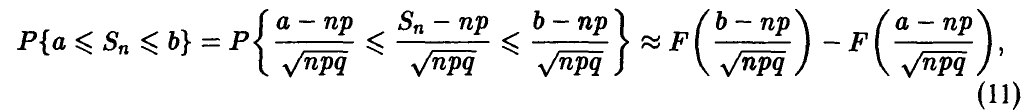
где 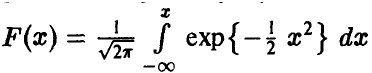— функция Лапласа.

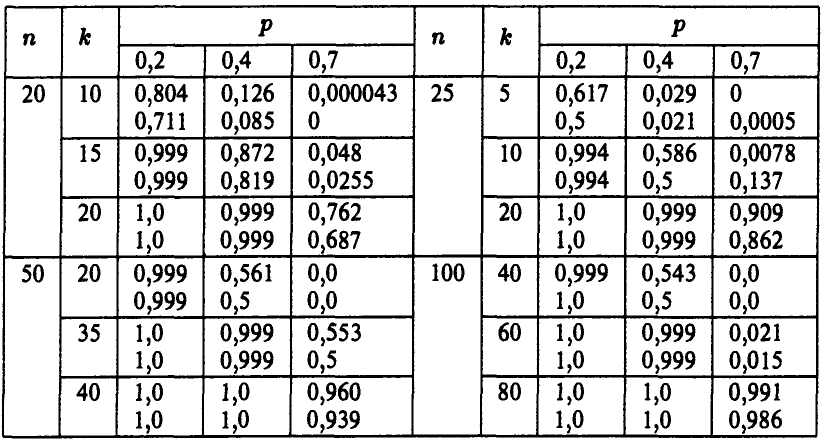
Уже при относительно небольших значениях n для средних (далеких от 0 и 1) значений р и q точность приближенного соотношения (11) достаточно высока. Приведенные ниже данные иллюстрируют порядок точности при замене совокупных биномиальных вероятностей по формуле (11) для различных значений n, р и k. В каждой ячейке таблицы в числителе приведено точное значение вероятности 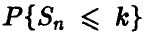, а в знаменателе — ее приближенное значение для соответствующих n, р и k.

Теперь мы можем уточнить закон больших чисел в форме Бернулли и получить не только качественные, но и содержательные количественные заключения.

Поскольку

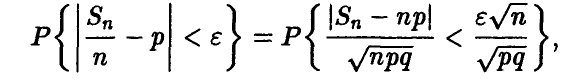
то, применяя соотношение (11) к последней вероятности, получаем

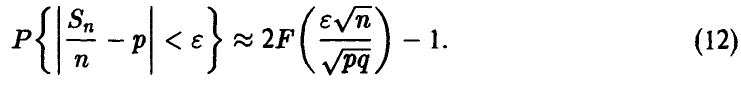
Формула (12) позволяет получать конкретные ответы на конкретные вопросы «Как часто?», «С какой точностью?», «При каком n?».

Пример:

Симметричную монету бросили 100 раз. Как часто число выпавших гербов будет отличаться от среднего не более чем на 10?

◄ Это прямой вопрос о величине вероятности

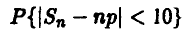
для п = 100 и р = 0,5. В соответствии с (12) имеем

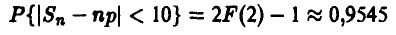
— в подавляющем большинстве случаев при 100 бросаниях симметричной монеты следует ожидать, что число выпавших гербов не меньше 40 и не больше 60. Отметим, что точное значение искомой вероятности равно 0,9540. ►

Пример:

Насколько большие отклонения частоты появления герба (в эксперименте с симметричной монетой) от 0,5 можно ожидать в подавляющем большинстве случаев, если монету бросили 50 раз? 100 раз?

◄ Вопрос задачи, это вопрос о величине є, удовлетворяющей условию

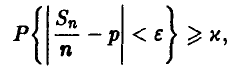
где 0 < х < 1 — величина вероятности, отвечающая нашим представлениям о том, как понимать «в подавляющем большинстве случаев». Конечно, хотелось бы положить х = 1, однако в этом случае ответ на вопрос тривиален: Е — любое число, не меньшее 1. Для получения нетривиальной информации о точности поступимся надежностью. Возьмем х близкое к единице настолько, чтобы событиями с вероятностью, меньшей 1-х, можно было пренебречь. Это, правда, даст нам возможность получить оценку для 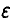, справедливую уже не для всех экспериментов, а только для х-доли из них. Но поскольку такие эксперименты достаточно часты (х взята близкой к единице!), постольку полученная информация о величине є оказывается информативной. Взяв, например, х = 0,9, получим для определения є неравенство

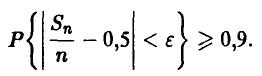
С учетом (12) это приводит к соотношению

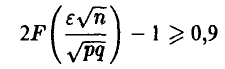
или

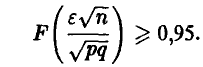
Полагая n = 50, 100, р = q = 0,5 и учитывая монотонное неубывание функции Лапласа, получаем

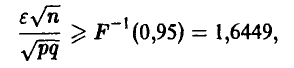
откуда

Для n = 50 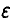не меньше 0,126, для n = 100 — 0,082. Из (13) очевидно, что с ростом n ожидаемые отклонения (при фиксированной надежности х) убывают пропорционально .

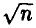Для заданной надежности при п = 100 точное решение поставленной задачи ►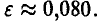

Пример:

Сколько раз следует бросить монету, чтобы не менее чем в 99 случаях из 100 наблюдаемая частота выпадения герба отличалась от вероятности не более чем на 0,01?

◄ Этот вопрос о количестве экспериментов, необходимых для оценивания неизвестной вероятности выпадения герба из неравенства

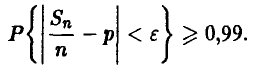
Соотношение (12) дает

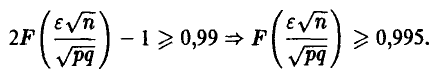
Заметим, что в силу неравенства

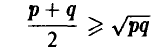
можно заключить, что

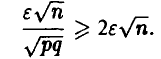
В силу монотонности функции Лапласа для любых р и q

Поэтому, если п удовлетворяет условию

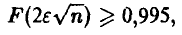
то подавно

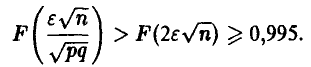
Определив n из последнего неравенства, мы заведомо решим поставленную задачу, может быть, и несколько завысив необходимое число экспериментов.

Несложные выкладки дают оценку

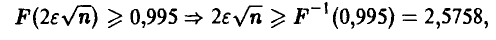
откуда для п получаем

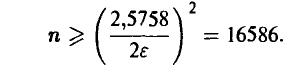
Столь большое количество экспериментов объясняется высокими требованиями к надежности, заданными условиями задачи. Если требование к надежности несколько снизить, то и оценка для n уменьшится. Так для х = 0,9 n ~ 6764, а для х= 0,8 n ~ 4106.

В заключение отметим, что в реальных экспериментах по оценке симметричности монеты наблюдались следующие результаты:

эксперимент Бюффона — 4040 бросаний, 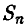= 2048, 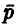= 0,5069;
эксперимент Пирсона ! — 12000 бросаний, 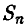= 6019, 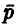= 0,5016;
эксперимент Пирсона !1 — 24000 бросаний, 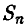= 12012, 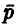= 0,5005. ►

Теорема Ляпунова

Теорема Муавра—Лапласа помимо возможности вычисления индивидуальных и совокупных биномиальных вероятностей предоставляет нам еще возможность по новому взглянуть на «взаимоотношение» различных классов случайных величин и их распределений. Действительно, соотношение (10) предыдущего пункта в форме

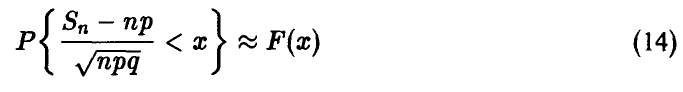
может быть прочитано как похожесть распределения центрированной и нормированной суммы независимых бернуллиевых случайных величин на нормальное распределение, что достаточно удивительно.

Еще более удивительным и неожиданным оказывается тот факт, что если взять не бернуллиевы, а любые другие случайные величины, то при весьма необременительных требованиях центрированная и нормированная их сумма будет иметь распределение, близкое к нормальному!

Точные утверждения, формализующие это наблюдение, носят в теории вероятностей название центральных предельных теорем, формулировке одной из которых мы посвятим этот пункт.

Может быть доказана следующая

Теорема:

Пусть 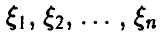, — независимые случайные величины с конечными математическими ожиданиями , дисперсиями 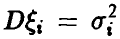, третьими моментами 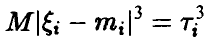и выполнено условие

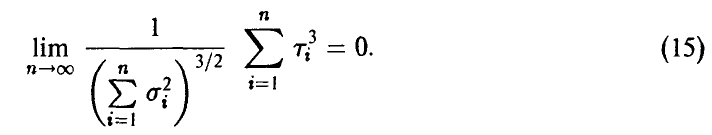
Тогда

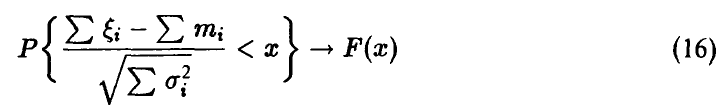
равномерно относительно х.

Отметим, что теорема не предъявляет никаких требований к законам распределения слагаемых! Важное условие (15) может быть интерпретировано как требование «приблизительной одинаковости» слагаемых.

Понятно, что без этого (или другого подобного) условия теорема перестает быть верной, ибо доминирующее слагаемое может подавить прочие слагаемые в сумме и тем самым будет определять ее распределение.

Для практических приложений весьма важен случай одинаково распределенных величин. В этом случае условия теоремы упрощаются — можно доказать, что если все 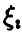— независимые одинаково распределенные случайные величины с конечными математическим ожиданием m и дисперсией 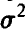, то (16) справедливо без дополнительного условия (15).

Теорема Ляпунова указывает на ту особую роль, которую в теории вероятностей и ее приложениях играет закон нормального распределения — сумма большого числа примерно одинаковых случайных слагаемых имеет почти нормальное распределение. Поэтому на практике, когда приходится изучать воздействия, обусловленные большим числом факторов, принимают обычно гипотезу о нормальном характере суммарного воздействия.

Как и теорема Муавра—Лапласа, теорема Ляпунова может служить источником формул для приближенного вычисления вероятностей, связанных с большими суммами случайных величин.

Пример:

Получим аналог соотношения (12) предыдущего пункта для закона больших чисел в форме Чебышева.

◄ Имеем

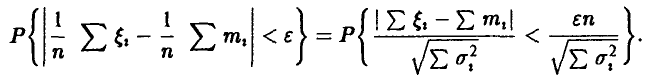
В силу соотношения (16) для последней вероятности при достаточно больших n получим

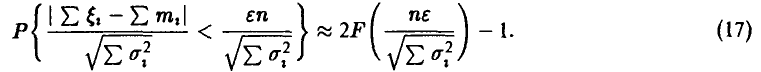
Это и есть искомое соотношение для вычисления вероятностей уклонений случайных средних от средних математических ожиданий. В случае одинаково распределенных слагаемых с конечными 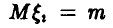и дисперсиями 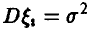соотношение (17) принимает вид

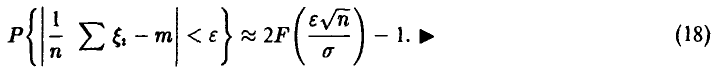
Пример:

Метод Монте-Карло вычисления интегралов.

Пусть требуется вычислить интеграл

Рассмотрим случайную величину 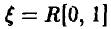и заметим, что интеграл (17) может быть представлен как 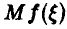. Поэтому, если 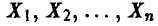— реализации случайной величины 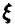, то, в силу закона больших чисел

Для оценки точности приближенного соотношения (20) нужно уметь оценивать величину

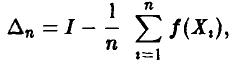
а для этого, в свою очередь, следует уметь решать неравенство

относительно 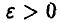при заданных значениях х и n. Если n достаточно велико, то в основу (21) может быть положено соотношение (18).

Действительно, 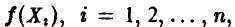— независимые, одинаково распределенные случайные величины, для которых 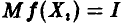. Поэтому

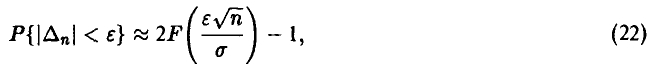
где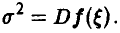

Для оценки величины 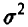заметим, что в силу интегрируемости функция f(x) ограничена — |f(x)| < а — и поэтому 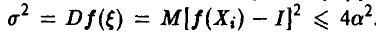. Отсюда, как и в примере 3 предыдущего пункта,

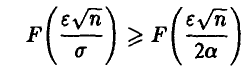
и из 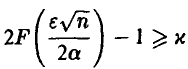следует, что заведомо и

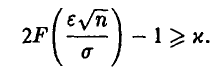
При фиксированном (и близком к единице) х для 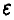имеем

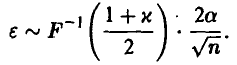
Таким образом, увеличивая n, мы в подавляющем большинстве случаев гарантируем (с надежностью х) точность є в вычислении интеграла (19) по формуле (20). ►

Примеры решения задач

1. Вероятность выбора точки из дуги полуокружности радиуса 1, с центром в начале координат, расположенной в правой полуплоскости, принимается пропорциональной длине проекции этой дуги на ось ОХ. Согласуется ли такое правило подсчета вероятностей с требованиями, предъявляемыми к вероятности?

Решение:

Нет, не согласуется. Нарушено правило сложения — для любых двух несовместных событий А и В должно выполняться Р{А+ В} = Р{А} + Р{В}. Пусть А — событие, состоящее в выборе точки из дуги, представляющей собой четверть окружности, лежащей в первой четверти, В — событие, состоящее в выборе точки из симметричной ей дуги, лежащей в четвертой четверти. Заметим, что А + В — достоверное событие и, следовательно, Р{ А + В} = 1. В соответствии с предлагаемым определением, Р{А} = Р{В} = Р{ А + В}, что возможно лишь если эти вероятности равны нулю, но последнее противоречит отмеченной выше достоверности события А + В.

2. Из множества точек, расположенных на отрезке [—2, 1] случайным образом выбирают точку и полагают вероятность выбора из подотрезка 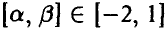пропорциональной 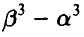. Согласуется ли такой способ подсчета вероятностей с требованиями, предъявляемыми к вероятности ?

Решение:

Да, согласуется. Действительно, из условия задачи

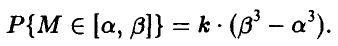
Условие нормировки вероятности позволяет определить значение коэффициента пропорциональности k:

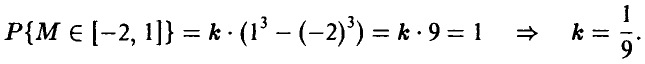
Пусть 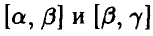— смежные подпромежутки основного промежутка. Тогда

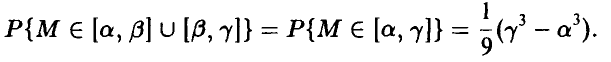
В то же время

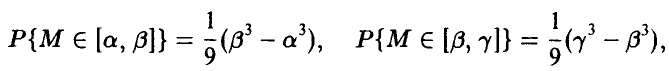
и в случае смежных промежутков правило сложения выполняется. Если же 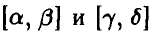— произвольные непересекающиеся промежутки (т. е. — несовместные события), то выполнение правила сложения следует из соотношения

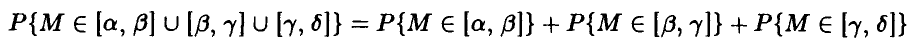
и следующего из него равенства

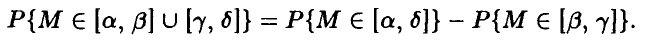
Прочие требования, предъявляемые к вероятности, легко устанавливаются.

3. Вероятность попадания точки M(p,q) в область F, лежащую в квадрате К = {(р, q): 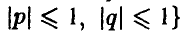, пропорциональна площади этой области: 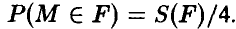. Найти вероятность того, что у уравнения 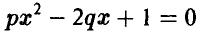нет действительных корней.

Решение:

Квадратное уравнение не имеет действительных корней, если его дискриминант отрицателен:

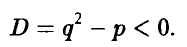
Следовательно

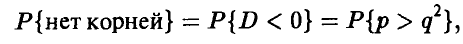
а последняя вероятность, в соответствии с условием задачи, пропорциональна площади множества 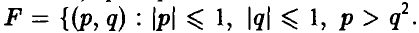Эта площадь равна (рис. 1)

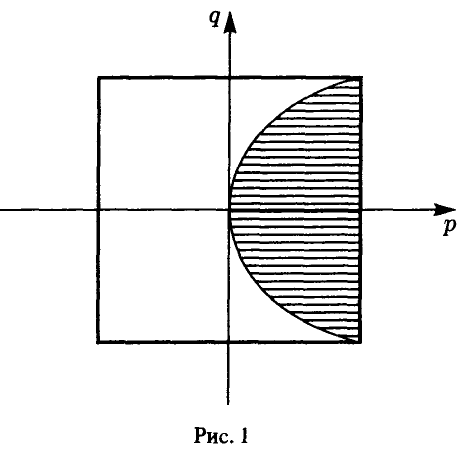
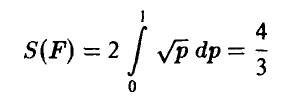
и, следовательно, искомая вероятность может быть найдена из соотношения

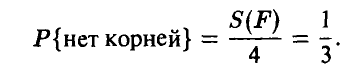
Из урны, содержащей всего 8 белых и черных шаров, извлекают одновременно два шара. Известно, что вероятность извлечения пары белых шаров в 15 раз больше вероятности извлечения пары черных. Можно ли по этим данным установить состав шаров в урне?

Решение:

Да, можно — в урне лежат 6 белых и 2 черных шара.

Действительно, пусть в урне m белых и 8 — m черных шаров. Вероятность извлечения пары белых шаров будет равна

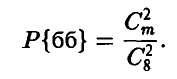
Аналогично, вероятность извлечения пары черных

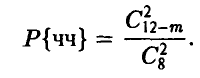
Из условия заключаем, что, поскольку Р{бб} = 15Р{чч}, постольку

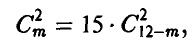
откуда получаем для m уравнение

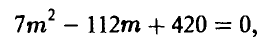
имеющее пару действительных корней 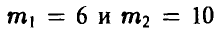. Второй корень не удовлетворяет условию, поскольку в урне всего 8 шаров.

5. Случайная величина 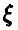имеет пуассоновское распределение и известно, что ее математическое ожидание т и дисперсия D связаны соотношением 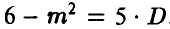. Найти вероятность .

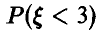Решение:

Известно, что математическое ожидание и дисперсия пуассоновского распределения совпадают и равны значению его параметра 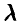. Условие задачи приводит к уравнению относительно :

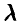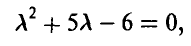
решениями которого являются числа 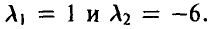Последнее значение не может быть параметром пуассоновского распределения в силу положительности параметра. Таким образом, случайная величина 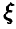имеет ряд распределения

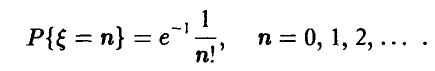
Для искомой вероятности получаем

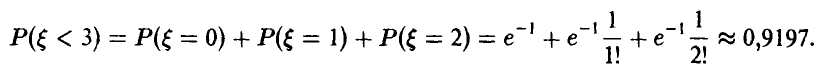
6. Плотность распределения случайной величины 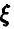непрерывна на всей прямой и дается соотношением:

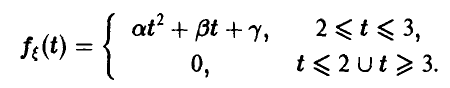
Найти параметры 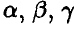, функцию распределения случайной величины 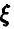, математическое ожидание случайной величины 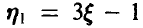, дисперсию 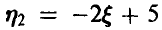и вероятность того, что 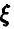не меньше 2,7.

Решение:

Непрерывность плотности на всей прямой позволяет сделать заключение о ее непрерывности в точках х = 2 и х = 3, откуда 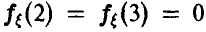. Условие нормировки плотности дает еще одно соотношение

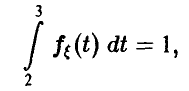
а вместе они приводят к системе уравнений относительно неизвестных параметров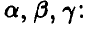

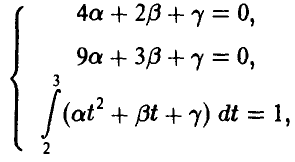
решение которой

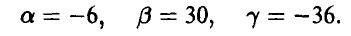
Функция распределения случайной величины 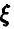дается соотношением

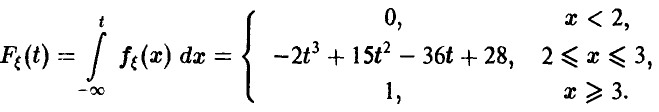
Заметим, что математическое ожидание случайной величины £, в силу симметрии плотности относительно точки t — 2,5, равно 2,5. Поэтому для математического ожидания случайной величины 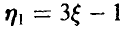получаем

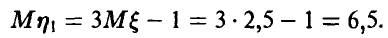
Для дисперсии случайной величины 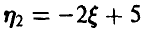имеем

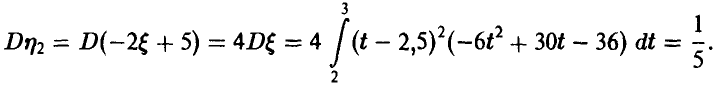
Наконец, вероятность того, что 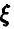не меньше 2,7 равна

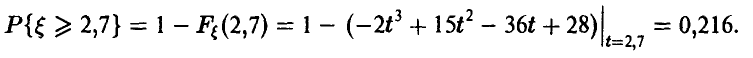
7. Функция распределения случайной величины 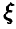непрерывна в R и дана соотношением

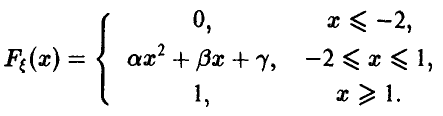
Известно, что случайная величина 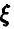неотрицательна с вероятностью 1/9. Найти значения постоянных 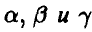, плотность распределения случайной величины математическое ожидание случайной величины 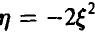, и вероятность того, что эта случайная величина заключена в пределах от — 1 до 0.

Решение:

Условие непрерывности функции распределения в точках х = — 2 и x = 1 дает

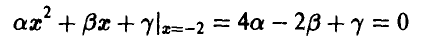
и

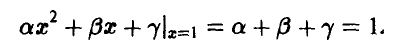
Присоединяя к ним условие

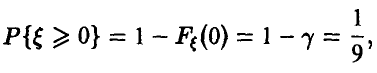
находим

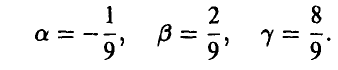
Плотность, очевидно, равна:

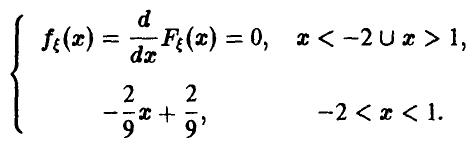
Матожидание случайной величины получим, используя теорему о математическом ожидании функции от случайной величины:

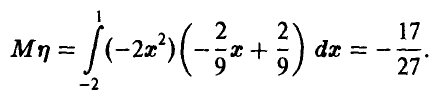
Ответ на последний вопрос задачи дают следующие рассуждения

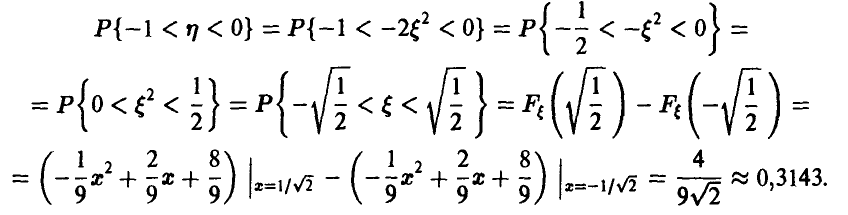
8. Функция распределения случайной величины 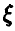дана соотношением

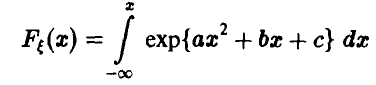
и известно, что 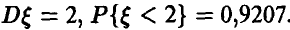Найти параметры а, b и с.

Решение:

Выделяя полный квадрат в показателе степени экспоненты, преобразуем выражение для функции распределения следующим образом

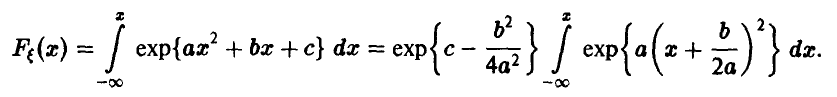
Поскольку

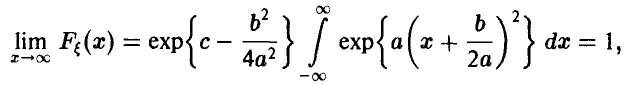
постольку несобственный интеграл сходится, что возможно лишь если а < 0. Полагая а=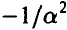, продолжим преобразования, сделав в интеграле замену переменных

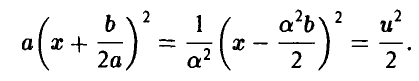
Получим

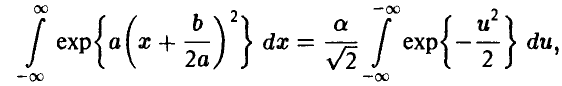
откуда, учитывая, что

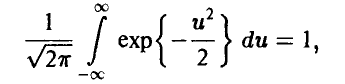
заключаем

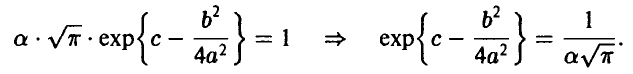
Функция распределения рассматриваемой случайной величины может быть, следовательно, представлена в виде

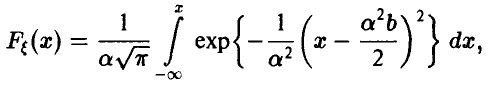
и значит, рассматриваемая случайная величина является нормальной с параметрами

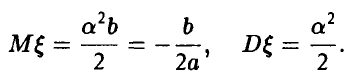
Из условия задачи получаем:

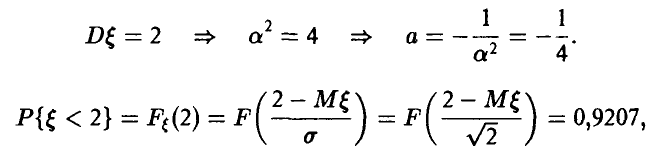
где F(x) — функция стандартного нормального распределения с параметрами (0, 1). Отсюда

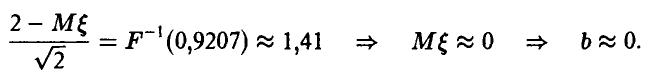
Для нахождения величины с используем полученное выше соотношение

9. Время безотказной работы некоторого узла сложного агрегата — экспоненциальная случайная величина со средним М = 2. Для увеличения надежности агрегата узел дублируется — ставят параллельно несколько одинаковых, но функционирующих независимо узлов. Сколько узлов следует запараллелить, чтобы с вероятностью не меньшей чем 0,9 по крайней мере один из них не вышел из строя за 10 часов работы?

Решение:

Т — случайное время безотказной работы узла — имеет экспоненциальное распределение. Это означает, что

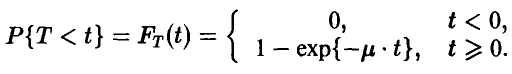
Известно, что математическое ожидание экспоненциальной случайной величины есть величина, обратная параметру: 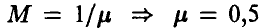. Следовательно, вероятность отказа узла в течение 10 часов будет равна

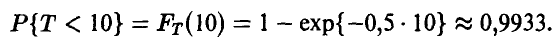
Если запараллелено N идентичных узлов, то событие А = {по крайней мере один из узлов не вышел из строя за 10 часов} является противоположным событию = {все узлы вышли из строя за 10 часов}. Поэтому Р{A} = 1 — Р{}. Для последней вероятности (в силу независимости отказов запараллеленных узлов) получаем

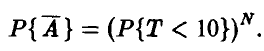
Искомое количество N может теперь быть найдено как наименьшее целое решение неравенства

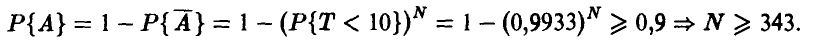
10. Случайное отклонение размера детали от номинального — нормальная случайная величина с параметрами m = 0, 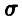= 1. Годными являются те детали, для которых отклонение заключено в пределах от — 1 до 1 мм. Найти функцию распределения отклонений для годных изделий.

Решение:

Пусть 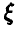— случайное отклонение размера детали от номинального: 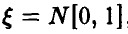, 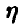— отклонение размера годной детали от номинального:

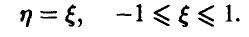
Для функции распределения случайной величины 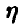получаем по определению (рис. 2)

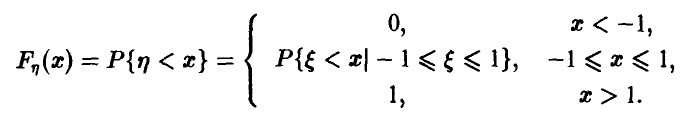
Вероятность же 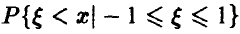равна

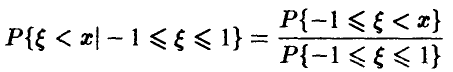
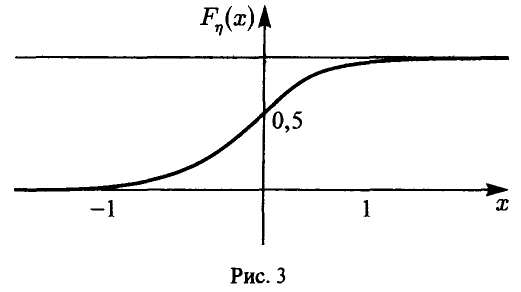
в соответствии с формулой условной вероятности. Таким образом, искомая функция распределения дается соотношением

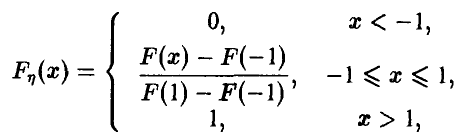
где F(x) — функция стандартного нормального распределения с параметрами 0 и 1. Находя значения F(-l) = 0,1587 и F(l) = 0,8413, окончательно получаем (рис. 3)

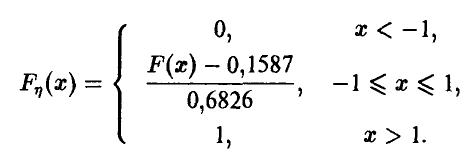
11. При сложении тысячи чисел каждое из них было округлено с точностью до 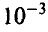. Предполагая, что ошибки округления слагаемых взаимно-независимы и равномерно распределены на промежутке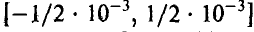, найти пределы, в которых будет лежать суммарная ошибка с надежностью, не худшей 0,997.

Решение:

Пусть 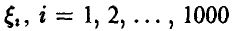— взаимно независимые случайные слагаемые, речь о которых идет в условии задачи. Задача состоит в отыскании таких значений 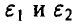, что

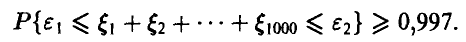
Учитывая симметрию рассматриваемой суммы относительно нуля, можно положить 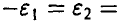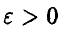. Таким образом, приходим к следующей задаче:

Найти значение 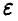такое, что

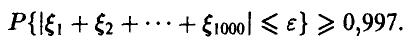
Для вычисления вероятности в левой части неравенства воспользуемся центральной предельной теоремой для одинаково распределенных слагаемых

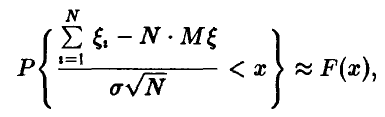
где F(x) — стандартная функция нормального распределения с параметрами (0, 1), N — достаточно большое число

Поскольку каждая из & равномерна на заданном промежутке 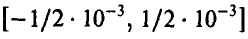, то

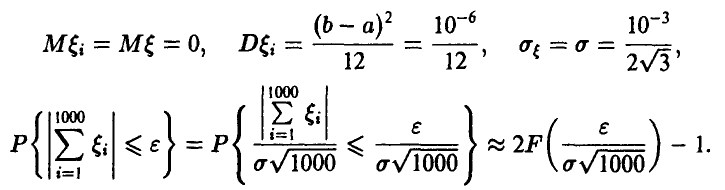
Последнее соотношение приводит к неравенству относительно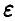

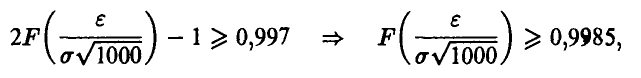
что в силу монотонности функции F(x) дает

12. При вычислении площади плоской фигуры D методом Монте-Карло поступают следующим образом:

Бросают случайно N точек внутрь квадрата К, полностью содержащего фигуру, площадь которой ищут.

Вероятность того, что точка, равномерно распределенная на квадрате К, попадает в область D, равна

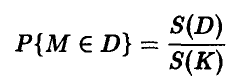
и, следовательно, искомая площадь может быть найдена из соотношения

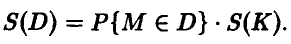
По теореме Бернулли, при достаточно большом числе N вероятность может быть приблизительно заменена частотой

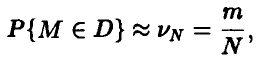
где m — число точек, попавших в область D. Для площади отсюда получаем приближенную формулу

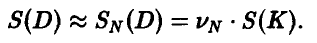
Сколько точек следует использовать для нахождения площади, чтобы не менее чем в 9 случаях из 10 точность 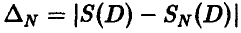была не хуже 1 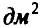, если известно, что ?

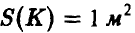Решение:

Задача сводится к определению значения N такого, что

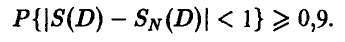
Заметим, что (ниже положено для сокращения записи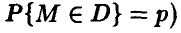

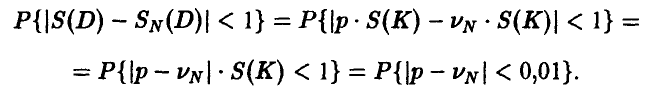
Теорема Бернулли для последней вероятности при больших значениях N дает оценку

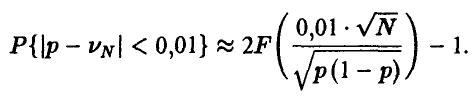
Таким образом, определению подлежит величина N (достаточно большая, чтобы последнее приближение было справедливо), удовлетворяющая неравенству

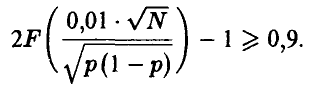
В таком виде это неравенство для своего решения относительно N требует знания величины 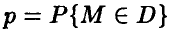, которая неизвестна, ибо ради ее определения и был задуман рассматриваемый эксперимент!

Мы предлагаем ниже два способа оценки значения N сверху, не являющиеся, конечно, точными, однако достаточно удобные с вычислительной точки зрения.

1. Первый способ связан с усилением основного неравенства в соответствии с нижеследующими рассуждениями:

Поскольку 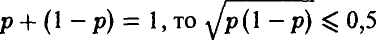и, следовательно,

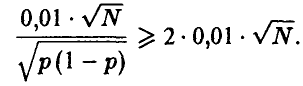
Функция F(-) монотонно возрастает, поэтому

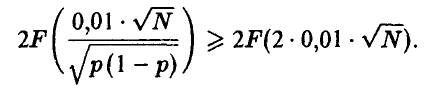
Отсюда, всякое значение N, удовлетворяющее неравенству

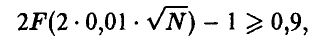
подавно удовлетворяет и неравенству

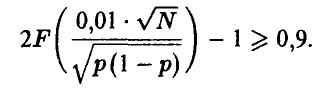
Предыдущее же неравенство легко разрешимо относительно N:

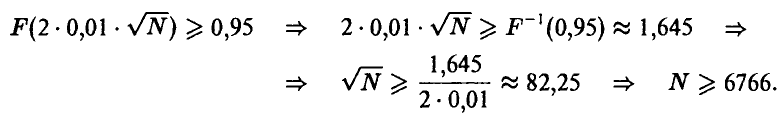
II. Второй способ связан с заменой неизвестной величины р ее оценкой 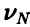. Основное неравенство при этом принимает вид

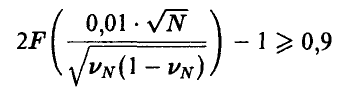
и легко разрешается

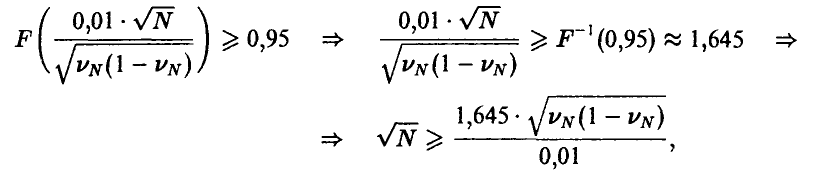
и окончательный ответ зависит от априорного (может быть и приблизительного) знания величины искомой площади

Так, если искомая площадь порядка половины площади квадрата, то 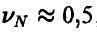, и ответ такой же, как и выше.

Если искомая площадь близка к площади квадрата, то 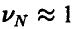и величина 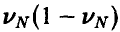мала, а вместе с ней мало и требуемое число экспериментов. Так, если, например 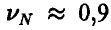, то 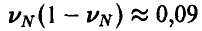и для N получаем

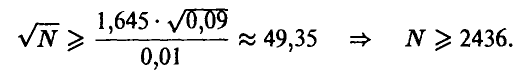
Вообще, приведенные выше выкладки показывают, что подобная процедура нахождения площадей плоских фигур тем эффективнее, чем большую часть объемлющего квадрата занимает множество D или его дополнение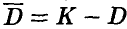

13. При проведении телепатического опыта индуктор независимо от предшествующих опытов выбирает с р = 0,5 один из двух предметов и думает о нем, а реципиент угадывает, о каком предмете думает индуктор. Опыт был повторен 100 раз и при этом было получено 58 правильных ответов. Какова вероятность правильного ответа в одном опыте, в предположении, что телепатической связи между индуктором и реципиентом нет ? Можно ли приписать наблюденный результат случайному совпадению или он говорит о наличии телепатической связи между индуктором и реципиентом?

Решение:

Пусть событие 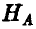состоит в том, что индуктор выбрал предмет А, событие 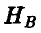он выбрал предмет В. Пусть, далее, события А и В означают, что реципиент выбрал соответствующий предмет

Если телепатической связи между индуктором и реципиентом нет, то в каждом из опытов

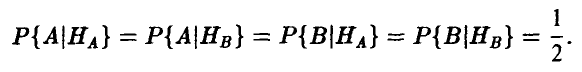
При этом вероятность Р{ У} угадывания реципиентом предмета, выбранного индуктором равна 0,5. Действительно, по формуле полной вероятности легко получить:

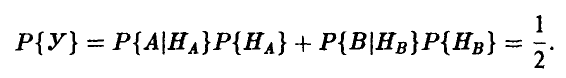
Если же телепатическая связь между индуктором и реципиентом есть, то вероятности 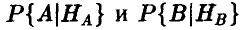должны быть больше 0,5 (соответственно, 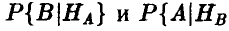} меньше 0,5), при этом и вероятность угадывания будет больше 0,5.

Следовательно, если телепатической связи между индуктором и реципиентом нет, то количество 51оо правильно угаданных ответов должно быть близко к 50. Если же количество правильно угаданных ответов будет сильно отличаться от 50 (в 100 опытах), то скорее всего всего это должно означать, что телепатическая связь между индуктором и реципиентом есть

Пусть 0 < а < 1 некоторая вероятность, настолько малая, что событиями, вероятность которых меньше а, можно пренебречь как практически невозможными4\ Предполагая, что телепатической связи между индуктором и реципиентом нет, определим, сколько же правильно угаданных ответов мы должны в этом случае наблюдать. И хотя логически понятно, что это может быть любое число от 0 до 100, скорее всего все-таки это будут числа, близкие к 50. Пусть 0 < k < 50 число, такое, что

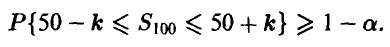
Тогда почти наверняка (с вероятностью, не меньшей чем 1 — а, т. е. в (1 — а) • 100 % случаев) мы будем наблюдать в эксперименте не менее чем 50 — k и не более чем 50 + k правильных угадываний.

Если наблюденное количество угадываний будет выходить за эти пределы, то объяснений этому может быть два:
— телепатии нет, но случайность процесса угадывания привела к такому значительному отклонению от среднего ожидаемого числа угадываний;
— такое значительное отклонение от среднего ожидаемого числа угадываний есть следствие наличия телепатической связи между индуктором и реципиентом.

И хотя логически оба рассуждения безупречны, мы, тем не менее, выберем второе, потому что выбор первого означает, что мы признаем возможность осуществления события с вероятностью 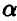, а это противоречит нашим исходным посылкам! Вероятность ошибки здесь в точности равна .

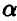Если же наблюденное количество угадываний будет входить в найденные пределы, то и этому может быть дано два различных объяснения:
— телепатии нет, и именно поэтому мы получили незначительное отклонение наблюденного числа угадываний от ожидаемого;
— телепатия есть, но случайно так получилось.

И здесь оба рассуждения логически безупречны, но мы выберем первое, ибо если наше предположение об отсутствии телепатии справедливо, то наблюденный результат должен наблюдаться почти всегда (с вероятностью 1 — 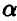, т. е. в (1 — 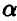) • 100 % случаев). Наша вероятность ошибиться будет зависеть в этом случае оттого, насколько силен предполагаемый телепатический эффект. Чем он сильнее, тем реже мы будем ошибаться.

Таким образом, для того чтобы получить ответ на вопрос задачи, следует определить пограничное значение k, описывающее возможные в подавляющем большинстве случаев в экспериментальной ситуации отклонения наблюденного числа угадываний от предполагаемого в случае отсутствия телепатической связи между индуктором и реципиентом. Для этого необходимо для заданного значения 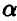решить относительно k неравенство

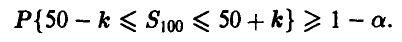
Заметим, что поскольку опыты проводятся независимо друг от друга и вероятность успеха (угадывания) в каждом опыте одна и та же, то количество успехов 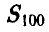является биномиальной случайной величиной с параметрами n = 100, р = 0,5 и вероятность, стоящая в левой части неравенства, равна

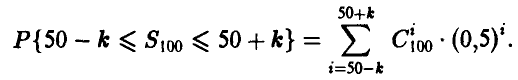
Применяя теорему Муавра—Лапласа, получаем

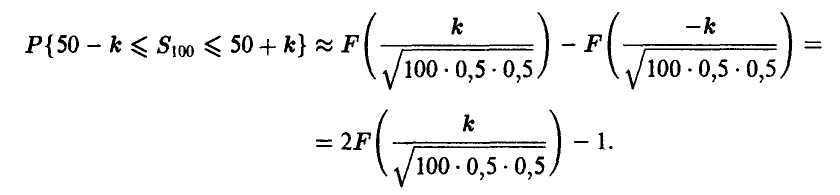
Последнее соотношение позволяет записать основное неравенство в виде

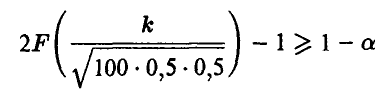
и решить его относительно k

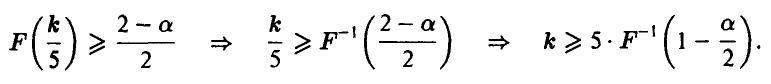
Граничные значения 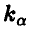, соответствующие различным значениям а, приведены ниже

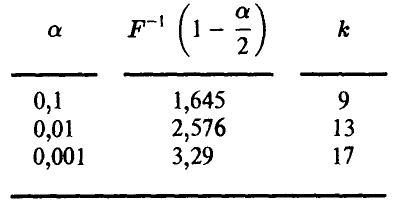
Таким образом, если телепатической связи между индуктором и реципиентом нет, то количество случайных угадываний будет в пределах от 41 до 59 с надежностью не худшей 0,9, от 37 до 63 с надежностью не худшей 0,99 и от 33 до 67 с надежностью не худшей 0,999.

Наблюденные в эксперименте 58 угадываний не дают оснований для вывода о наличии телепатической связи — результат может быть объяснен случайным совпадением.

Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Статистические оценки
6. Статистическая проверка гипотез
7. Статистическое исследование зависимостей
8. Теории игр
9. Вероятность события
10. Теорема умножения вероятностей
11. Формула полной вероятности
12. Теорема о повторении опытов
13. Нормальный закон распределения
14. Определение законов распределения случайных величин на основе опытных данных
15. Системы случайных величин
16. Нормальный закон распределения для системы случайных величин
17. Вероятностное пространство
18. Классическое определение вероятности
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность