Закон сохранения массы

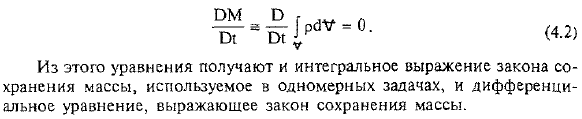
Закон сохранения массы

Закон сохранения массы. Выберите управляющий объем V в пространстве, окруженном любой поверхностью A. пусть плотность жидкости p зависит как от времени, так и от координат. р =(р, л)= п(х, г, р, 1). Масса бесконечно малого объема, расположенного в точке с координатами r-(x, y, g) в точке I, равна массе объема V жидкости на поверхности A, равной p (g, g) М = / №РС. (4.1).

Согласно закону сохранения массы при перемещении рассматриваемого объема V1 его масса не изменяется. Людмила Фирмаль

• Закон сохранения массы может быть выражен следующим образом, так как изменение во времени гидродинамических величин, связанных с определенным удельным объемом движения жидкости, выражается в существенной дифференциации этой величины. Семьдесят семь Это уравнение дает как интегральное представление закона сохранения массы, используемого в задаче 1D, так и дифференциальное уравнение, представляющее закон сохранения массы.

Поэтому при учете массы веществ необходимо принимать во внимание прирост или уыбль, отвечающие поглощению или выделению энергии при данной реакции. Людмила Фирмаль

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Потенциал скорости и функция тока при плоском безвихревом движении.
2. Основы гидродинамики. Предварительные сведения.
3. Закон изменения количества движения.
4. Закон изменения момента количества движения.