Распределение вероятностей называют равномерным, если на интервале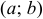 
, которому принадлежат все возможные значения случайной величины 
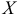, плотность распределения сохраняет постоянное значение, а именно
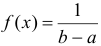; вне этого интервала 
.
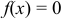Математическое ожидание случайной величины, равномерно распределенной в интервале 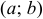, равно полусумме концов этого интервала 
.
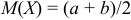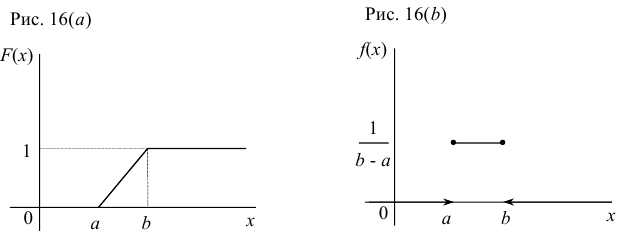
График функции равномерного распределения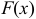 
изображен на рис. 16(a), а график плотности распределения 
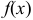— на рис. 16(b).
Пример:
Найти математическое ожидание и дисперсию случайной величины 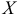равномерно распределенной в интервале (1; 6).
Решение:
Плотность вероятности равномерного распределения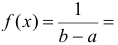 
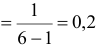. Используем формулу 
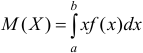. Подставив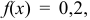 
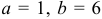, получим 
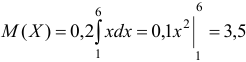. Этот же результат можно получить, используя свойство равномерно распределенной случайной величины 
.
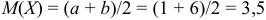Найдем дисперсию по формуле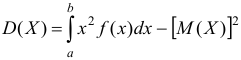 
,
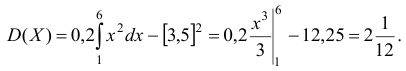
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:
