Нормальный закон распределения и его параметры с примерами решения и образцами выполнения

Нормальный закон распределения и его параметры:

Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это — наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых — элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.

Теоремы, устанавливающие нормальный закон как предельный для суммы независимых равномерно малых случайных слагаемых, будут подробнее рассмотрены в главе 13.

Нормальный закон распределения характеризуется плотностью вероятности вида:

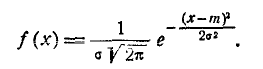(6.1.1)

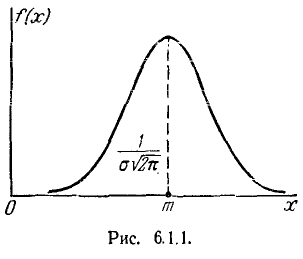
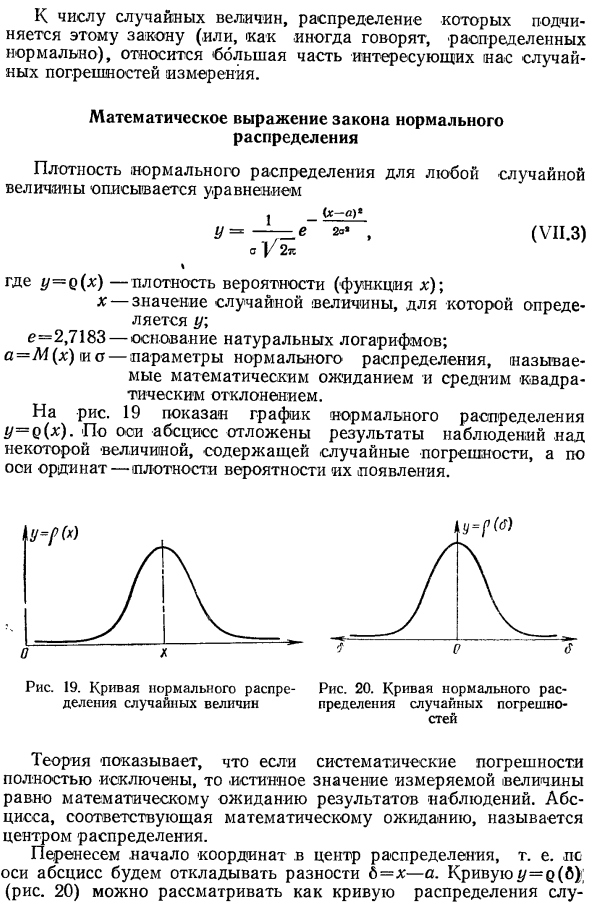
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 6.1.1). Максимальная ордината кривой, равная 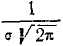, соответствует точке х = m по мере удаления от точки m плотность распределения падает, и при кривая асимптотически приближается к оси абсцисс.

Выясним смысл численных параметров т и о, входящих в выражение нормального закона (5.1.1); докажем, что величина m есть не что иное, как математическое ожидание, а величина 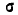— среднее квадратическое отклонение величины X. Для этого вычислим основные числовые характеристики величины X — математическое ожидание и дисперсию.

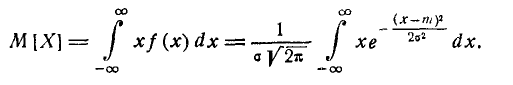
Применяя замену переменной

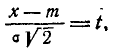
имеем:

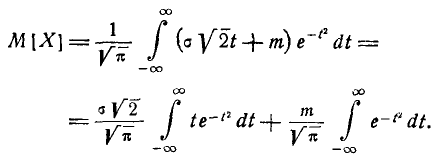(6.1.2)

Нетрудно убедиться, что первый из двух интервалов в формуле (5.1.2) равен нулю; второй представляет собой известный интеграл Эйлера — Пуассона:

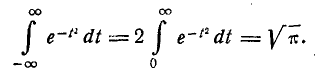(6.1.3)

Следовательно, М[Х] = m

т. е. параметр m представляет собой математическое ожидание вели- величины X. Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно — ц. р.). Вычислим дисперсию величины X:

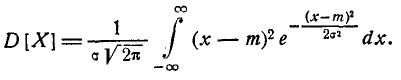
Применив снова замену переменной

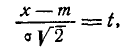
имеем:

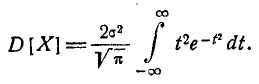
Интегрируя по частям, получим:

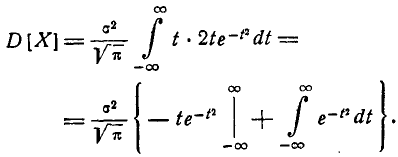
Первое слагаемое в фигурных скобках равно нулю (так как 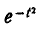При 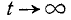убывает быстрее, чем возрастает любая степень f), второе слагаемое по формуле 5.1.3) равно 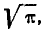откуда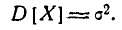

Следовательно, параметр о в формуле 5.1.1) есть не что иное, как среднее квадратическое отклонение величины X.

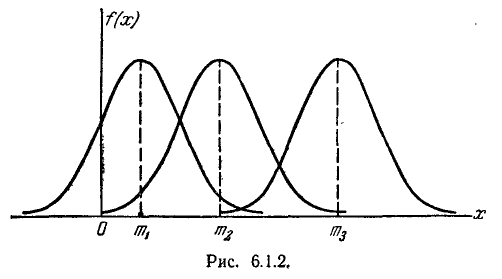
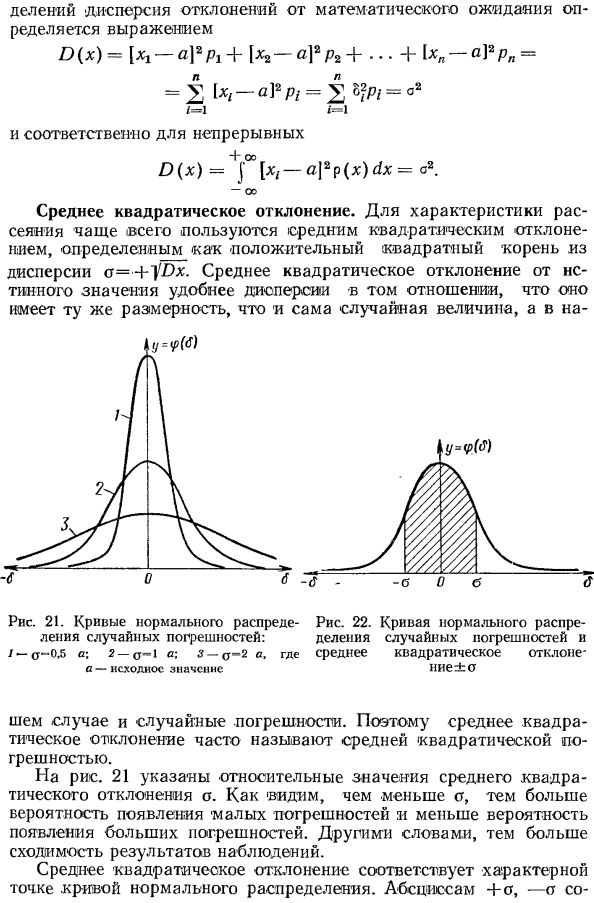
Выясним смысл параметров m и 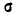нормального распределения. Непосредственно из формулы 5.1.1) видно, что центром симметрии распределения является центр рассеивания m. Это ясно из того, что при изменении знака разности (х — m) на обратный выражение 5.1.1) не меняется. Если изменять центр рассеивания т. кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.

Размерность центра рассеивания—та же, что размерность случайной величины X.

Параметр о характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна 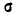; при увеличении 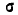максимальная ордината уменьшается. Так как площадь

кривой распределения всегда должна оставаться равной единице, то при увеличении о кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении 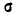кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 6.1.3 показаны три нормальные кривые (/, //, ///) при m=0; из них кривая l соответствует

самому большому, а кривая /// — самому малому значению . Изменение параметра 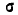равносильно изменению масштаба кривой распределения— увеличению масштаба по одной оси и такому же уменьшению по другой.

Размерность параметра 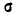, естественно, совпадает с раpмерноcтью случайной величины X.

В некоторых курсах теории вероятностей в качестве характеристики рассеивания для нормального закона вместо среднего квадратического отклонения применяется так называемая мера точности. Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению :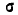

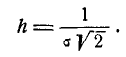
Размерность меры точности обратна размерности случайной величины.

Термин «мера точности» заимствован из теории ошибок измерений: чем точнее измерение, тем больше мера точности. Пользуясь мерой точности h, можно записать нормальный закон в виде: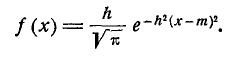

Моменты нормального распределения

Выше мы доказали, что математическое ожидание случайной вели- величины, подчиненной нормальному закону 6.1.1), равно m, а среднее квадратическое отклонение равно .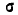

Выведем общие формулы для центральных моментов любого порядка.

По определению:

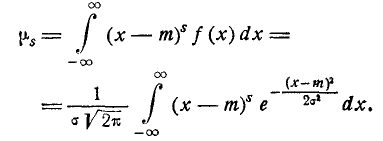
Делая замену переменной

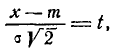
получим:

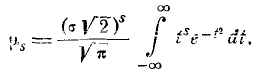(6.2.1)

Применим к выражению (6.2.1) формулу интегрирования по частям: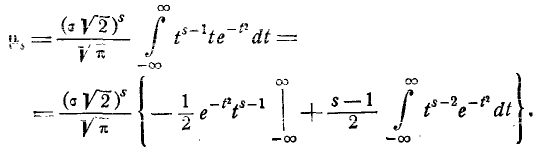

Имея в виду, что первый член внутри скобок равен нулю, получим: 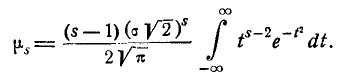(6.2.2)

Из формулы (6.2.1) имеем следующее выражение для 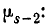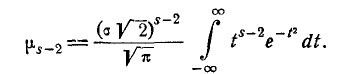(6.2.3)

Сравнивая правые части формул (6.2.2) и (6.2.3), видим, что они отличаются между собой только множителем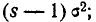 следовательно,

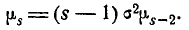(6.2.4)

Формула (6.2.4) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что 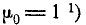и можно вычислить центральные моменты всех порядков. Так как то из формулы (6.2.4) следует, что все нечетные моменты нормального распределения равны нулю. Это, впрочем, непосредственно следует из симметричности нормального закона.

Для четных s из формулы (6.2.4) вытекают следующие выражения для последовательных моментов:

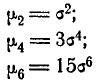
и т. д. Общая формула для момента s-гo порядка при любом четном s имеет вид:

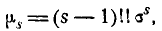
где под символам (s—1)!! понимается произведение всех нечетных чисел от 1 до s— 1. Так как для нормального закона то асимметрия его также равна нулю:

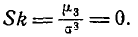
Из выражения четвертого момента

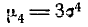
имеем:

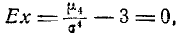
‘) Нулевой момент любой случайной величины равен единице как математическое ожидание нулевой степени этой величины.

т. е. эксцесс нормального распределения равен нулю. Это и естественно, так как назначение эксцесса — характеризовать сравнительную крутость данного закона по сравнению с нормальным.

Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения

Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X, подчиненной нормальному закону с параметрами m, 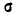, на участок от а до 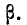Для вычисления этой вероятности воспользуемся общей формулой

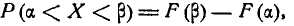(6.3.1)

где F (х)— функция распределения величины X.

Найдем функцию распределения F(x) случайной величины X, распределенной по нормальному закону с параметрами m, 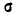. Плот- Плотность распределения величины X равна:

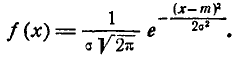(6.3.2)

Отсюда находим функцию распределения

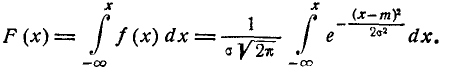(6.3.3)

Сделаем в интеграле (6.3.3) замену переменной

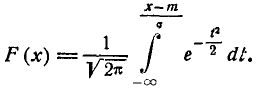(6.3.4)

и приведем его к виду:

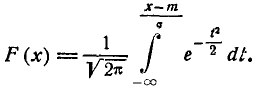(6.3.4)

Интеграл (6.3.4) не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения 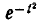или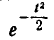 (так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:

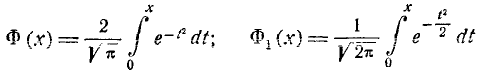
и т. д. Какой из этих функций пользоваться — вопрос вкуса. Мы выберем в качестве такой функции

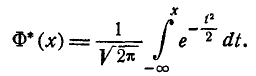(6.3.5)

Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами от m = 0, 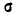=1.

Условимся называть функцию Ф*(х) нормальной функцией распределения. В приложении (табл. 1) приведены таблицы значений функции Ф*(х)

Выразим функцию распределения (6.3.3) величины X с пара- параметрами m и через нормальную функцию распределения Ф*(х). Очевидно,

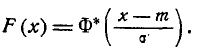(6.3.6)

Теперь найдем вероятность попадания случайной величины X на участок от а до 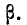Согласно формуле (6.3.1)

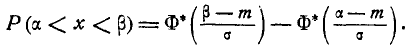(6.3.7)

Таким образом, мы выразили вероятность попадания на участок случайной величины X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения Ф* (х), соответствующую простейшему нормальному . закону с параметрами 0,1. Заметим, что аргументы функции Ф* в фор- формуле (6.3.7) имеют очень простой смысл: 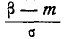есть расстояние от правого конца участка 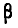до центра рассеивания, выраженное в средних квадратических отклонениях; 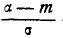— такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания , и отрицательным, если слева.

Как и всякая функция распределения,, функция Ф*(х) обладает свойствами:

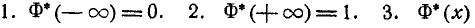-неубывающая функция

Кроме того, из симметричности нормального распределения с параметрами m = 0, 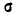=1 относительно начала координат следует, что

ф* (— х)=1— Ф* (х). (6.3.8)

Для облегчения интерполяции в таблицах рядом со значениями функции приведены ее приращения за один шаг таблиц

Пользуясь этим свойством, собственно говоря, можно было бы ограничить таблицы функции Ф(х) только положительными значениями аргумента, но, чтобы избежать лишней операции (вычитание из единицы), в таблице 1 приложения приводятся значения Ф(х) как для положительных, так и для отрицательных аргументов.

На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания m. Рассмотрим такой участок длины 2l (рис. 6.3.1). Вычислим вероятность попадания на этот участок по формуле (6.3.7):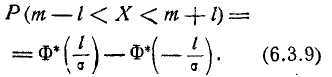

Учитывая свойство (6.3.8) функции Ф*(х) и придавая левой части формулы (6.3.9) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону, на участок, симметричный относительно центра рассеивания:

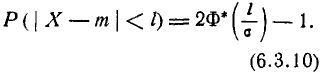
Решим следующую задачу. Отложим от центра рассеивания m последовательные отрезки длиной (рис. 6.3.2) и вычислим вероятность попадания случайной величины X в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону.

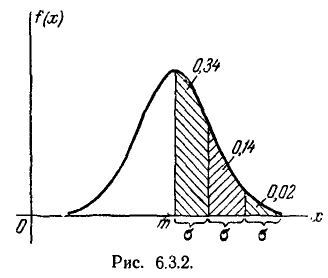
По формуле (6.3.7) находим:

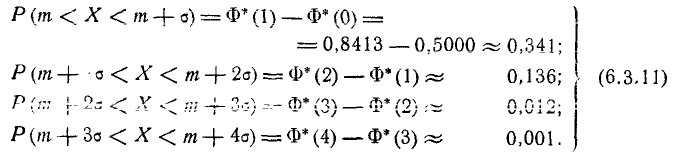
Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т. д.) с точностью до 0,001 равны нулю.

Округляя вероятности попадания в отрезки до 0,01 (до 1%). получим три числа, которые легко запомнить: 0,34; 0,14; 0,02.

Сумма этих трех значений равна 0,5. Это значит, что для нормально распределенной случайной величины все рассеивание (с точностью до долей процента) укладывается на участке m± З.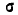

Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма«. Из правила трех сигма вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения .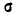

Пример:

Случайная величина X, распределенная по нормальному закону, представляет собой ошибку измерения некоторого расстояния. При измерении допускается систематическая ошибка в сторону завышения на 1,2 (м)\ среднее квадратическое отклонение ошибки измерения равно 0,8 (м). Найти вероятность того, что отклонение измеренного значения от истинного не превзойдет по абсолютной величине 1,6 (м).

Решение:

Ошибка измерения есть случайная величина X, подчинен- подчиненная нормальному закону с параметрами m= 1,2 и 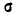= 0,8. Нужно найти вероятность попадания этой величины на участок от а =—1,6 до 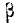= + 1,6. По формуле (6.3.7) имеем:

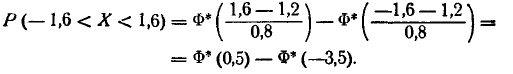
Пользуясь таблицами функции Ф* (х) (приложение, табл. 1), найдем:

Ф* (0,5) = 0,6915; Ф* (—3,5) = 0,0002,

откуда Р (—1,6 < X < 1,6) = 0,6915 — 0,0002 = 0,6913 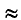0,691.

Пример:

Найти ту же вероятность, что в предыдущем примере, но при условии, что систематической ошибки нет.

Решение:

По формуле (6.3.10), полагая l=1.6, найдем:

Пример:

По цели, имеющей вид полосы (автострада), ширина которой равна 20 м, ведется стрельба в направлении, перпендикулярном автостраде, прицеливание ведется по средней линии автострады. Среднее квадратическое отклонение в направлении стрельбы равно = 8 м. Имеется систематическая ошибка в направлении стрельбы: недолет 3 м. Найти вероятность попадания в автостраду при одном выстреле.

Решение:

Выберем начало координат в любой точке на средней линии автострады (рис. 6.3.3) и направим ось абсцисс перпендикулярно автостраде. Попадание или непопадание снаряда в автостраду определяется значением только одной координаты точки падения X (другая координата Y нам безразлична). Случайная величина X распределена по нормальному закону

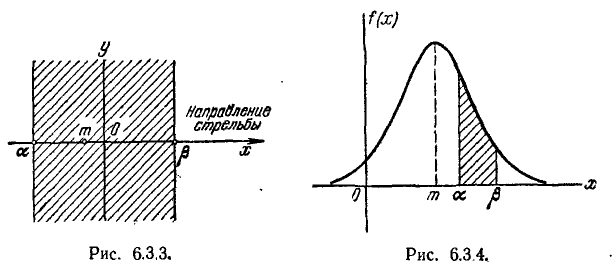
с параметрами m = —3, = 8. Попадание снаряда в автостраду соответствует попаданию величины X на участок от а = — 10 до = 4-10. Применяя формулу (6.3.7), имеем:

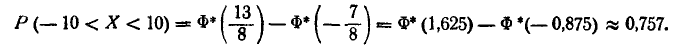
Пример:

Имеется случайная величина Х, нормально распределенная, с центром рассеивания m (рис. 6.3.4) и некоторый участок 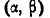оси абсцисс. Каково должно быть среднее квадратическое отклонение о случайной величины X для того, чтобы вероятность попадания р на участок 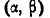достигала максимума?

Решение:

Имеем:

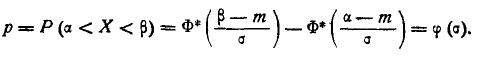
Продифференцируем эту функцию величины :

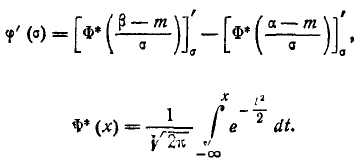
Применяя правило дифференцирования интеграла по переменной, входящей в его предел, получим:

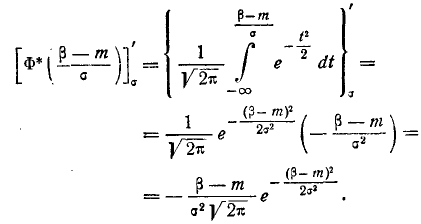
Аналогично

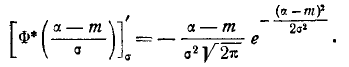
Для нахождения экстремума положим:

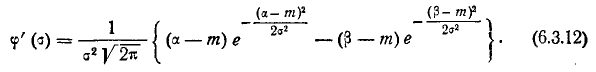
При 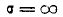это выражение обращается в нуль и вероятность р достигает минимума. Максимум р получим из условия 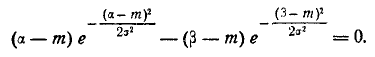(6.3.13)

Уравнение (6.3.13) можно решить численно или графически.

6.4. Вероятное (срединное) отклонение

В ряде областей практических применений теории вероятностей (в частности, в теории стрельбы) часто, наряду со средним квадратическим отклонением, пользуются еще одной характеристикой рассеивания, так называемым вероятным, или срединным, отклонением. Вероятное отклонение обычно обозначается буквой Е (иногда В).

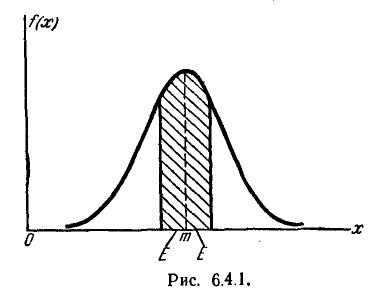
Вероятным (срединным) отклонением случайной величины X, распределенной по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна половине.

Геометрическая интерпретация вероятного отклонения показана на рис. 6.4.1. Вероятное отклонение Е — это половина длины участка оси абсцисс, симметричного относительно точки m, на кото- который опирается половина площади кривой распределения.

Поясним смысл термина «срединное отклонение» или «срединная ошибка», которым часто пользуются в артиллерийской практике вместо «вероятного отклонения».

Рассмотрим случайную величину X, распределенную по нормальному закону. Вероятность того, что она отклонится от центра рассеивания m меньше чем на Е, по определению вероятного отклонения Е, равна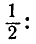

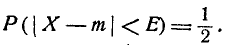(6.4.1)

Вероятность того, что она отклонится от m больше чем на Е, тоже равна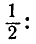

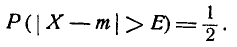
Таким образом, при большом числе опытов в среднем половина значений случайной величины X отклонится от m больше чем на Е, а половина — меньше. Отсюда и термины «срединная ошибка», «срединное отклонение».

Очевидно, вероятное отклонение, как характеристика рассеивания, должно находиться в прямой зависимости от среднего rвадратического отклонения 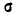. Установим эту зависимость. Вычислим вероятность события | X — m | < Е в уравнении (6.4.1) по формуле (6.3.10). Имеем:

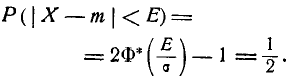
Отсюда

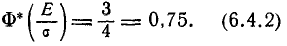
По таблицам функции Ф* (х) можно найти такое значение аргумента х, при котором она равна 0,75. Это значение аргумента приближенно равно 0,674; отсюда

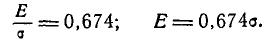(6.4.3)

Таким образом, зная значение 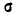, можно сразу найти пропорциональное ему значение Е. Часто пользуются еще такой формой записи этой зависимости:

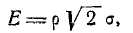(6.4.4)

где р — такое значение аргумента, при котором одна из форм интеграла вероятностей — так называемая функция Лапласа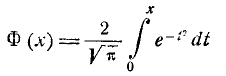

— равна половине. Численное значение величины р приближенно равно 0,477.

В настоящее время вероятное отклонение, как характеристика рассеивания, все больше вытесняется более универсальной характеристикой 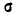. В ряде областей приложений теории вероятностей она сохраняется лишь по традиции.

Если в качестве характеристики рассеивания принято вероятное отклонение Е, то плотность нормального распределения записывается в виде:

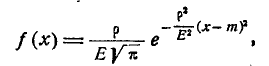(6.4.5)

а вероятность попадания на участок от а до 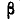чаще всего записывается в виде:

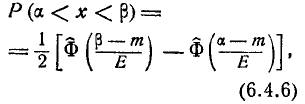
где

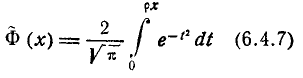— так называемая приведенная функция Лапласа.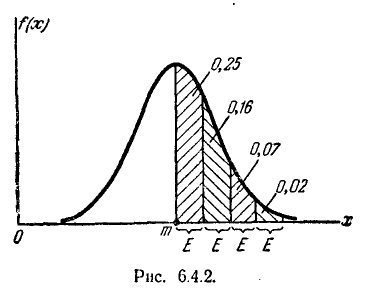

Сделаем подсчет, аналогичный выполненному в предыдущем п° для среднего квадратического отклонения 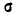: отложим от центра рассеивания т. последовательные отрезки длиной в одно вероятное отклонение Е (рис. 6.4.2) и подсчитаем вероятности попа- попадания в эти отрезки с точностью до 0,01. Получим: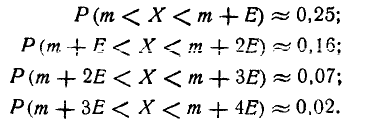

Отсюда видно, что с точностью до 0,01 все значения нормально распределенной случайной величины укладываются на участке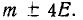

Пример:

Самолет-штурмовик производит обстрел колонны войск противника, ширина которой’ равна 8 м. Полет — вдоль колонны, прицеливание— по средней линии колонны; вследствие скольжения имеется систематическая ошибка: 2 м вправо но направлению полета. Главные вероятные отклонения: по направлению полета 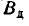= 15 м, в боковом направлении 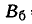= 5 М. Не имея в своем распоряжении никаких таблиц интеграла вероятностей, а зная только числа:

25%, 16%, 7%, 2%,

оценить грубо-приближенно вероятность попадания в колонну при одном выстреле и вероятность хотя бы одного попадания при трех независимых выстрелах.

Решение:

Для решения задачи достаточно рассмотреть одну координату точки попадания — абсциссу X в направлении, перпендикулярном колонне. Эта абсцисса распределена по нормальному закону с центром рассеивания m = 2 и вероятным отклонением 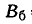=Е = 5 (м). Отложим мысленно от центра рассеивания в ту и другую сторону отрезки длиной в 5 м. Вправо от центра рассеивания цель занимает участок 2 м, который составляет 0,4 вероятного отклонения. Вероятность попадания на этот участок приближенно равна:

0,4-25% =0,1.

Влево от центра рассеивания цель занимает участок б м. Это — целое вероятное отклонение E м), вероятность попадания в которое равна 25% плюс часть длиной 1 м следующего (второго от центра) вероятного отклонения, вероятность попадания в которое равна 16%. Вероятность попадания в часть длиной 1 м приближенно равна: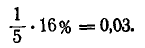

Таким образом, вероятность попадания в колонну приближенно равна:

0,1+0,25 + 0,03 = 0,38.

Вероятность хотя бы одного попадания при трех выстрелах равна: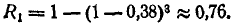

Закон нормального распределения случайных величин

Смотрите также:

Распределения дискретных величин	Математическое выражение закона нормального распределения
Распределение непрерывных случайных величин	Свойства и характеристики распределения случайных погрешностей

Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Статистическое исследование зависимостей
9. Теории игр
10. Вероятность события
11. Теорема умножения вероятностей
12. Формула полной вероятности
13. Теорема о повторении опытов
14. Определение законов распределения случайных величин на основе опытных данных
15. Системы случайных величин
16. Нормальный закон распределения для системы случайных величин
17. Вероятностное пространство
18. Классическое определение вероятности
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность