Оглавление:


Закон Архимеда. Плавание тел
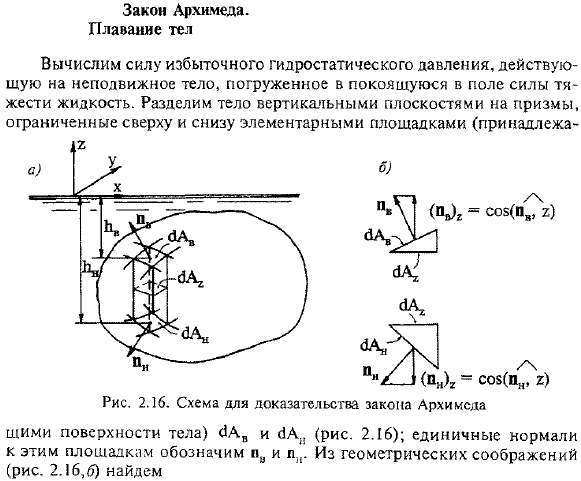
Закон Архимеда. Плавание тел. Поверхности тела) dAv и 6AN (рис. 2.16); единичные нормали этих участков обозначены pc и pi. Исходя из геометрических соображений (рис. 2.16.6), 44 Аль. Аль. н ■ХГ» * «= АА » (ПВ) 2 = Аа2; = ОА»(Пн) 2-ал2. «{■С * (2.57) Где JA2-площадь поперечного сечения призмы по горизонтальной плоскости. Знак минус 2-го выражения (2.57) связан с вектором mon, находящимся вниз и (mon) 0. Рассмотрим сумму поверхностных сил, действующих на выбранную базовую призму. (2.8) согласно сайту c! Сила гидростатического давления для Av и Ya ^равна следующим значениям: = п. РВ ^ А,. (2-58) Где избыточное гидростатическое давление РВ = pE2B, пн-п $ \ ХІ = PE2H.
Тело, которое плавает в неустойчивом равновесном состоянии, но слегка покачивается вбок, возвращается в исходное положение. Людмила Фирмаль
- На вертикальную плоскость призмы воздействует сила от соседней призмы, сумма которой равна Проекция всех поверхностных сил, действующих на призму, на ось z、 (1па) 2 =(АРВ) г +(АРВ) 2+(нет. ж)г. (2.60).) (2.58)、(2.59)、(2.60)、и (2.57) присваивается этому уравнению、 (Ара) 2-P82H 1А2 +(1Pvg)2-(2.61) Запишите аналогичное уравнение для всех основных призм, на которые делится объект интереса, и добавьте все эти equations. In в этом случае силы взаимодействия соседних призм вдоль вертикальной плоскости взаимно отменяют друг друга, а члены (rvr) r взаимно отменяют друг друга. Сумма первых 2 членов представляет собой вес жидкости в объеме призмы ПВ (ПВ-2М) ЭГ-р§с№, (2.62) Где YY = 2k) yA2-объем призмы.
Таким образом, подставляя (2.61) в (2.62), в результате получаем сумму всех основных сил (sPa) 2、 (па) Р = Пе^, (2.63) Где V = / yU-объем тела. Формула (2.63) представляет собой известный закон Архимеда: на неподвижный объект, погруженный в жидкость в гравитационном поле, воздействует плавучесть, равная весу жидкости в объеме данного объекта. Эту силу иногда называют Архимедом. Проведя аналогичные расчеты (то есть разделив объект на основную призму в плоскости, параллельной осям x и y), можно доказать почти очевидный факт-сумма горизонтальных составляющих силы избыточного гидростатического давления, действующей на погруженный объект, будет равна нулю. Сорок пять.
- Точка действия силы (выдавливания) Архимеда называется центром смещения. Если тело однородно, мы можем доказать, что центр смещения тела совпадает с центром тяжести тела (относительно просто, необходимо только использовать полученную теорему). Если вес больше, чем плавучесть, тело мертво. Если вес равен плавучести, то тело плавает в жидкости. Если вес меньше плавучести, поднимаясь вверх и достигая свободной поверхности, то плавучесть, действующая на подводную часть, равна весу. При рассмотрении плавающего тела вас интересует вопрос об устойчивости плавающего тела body.
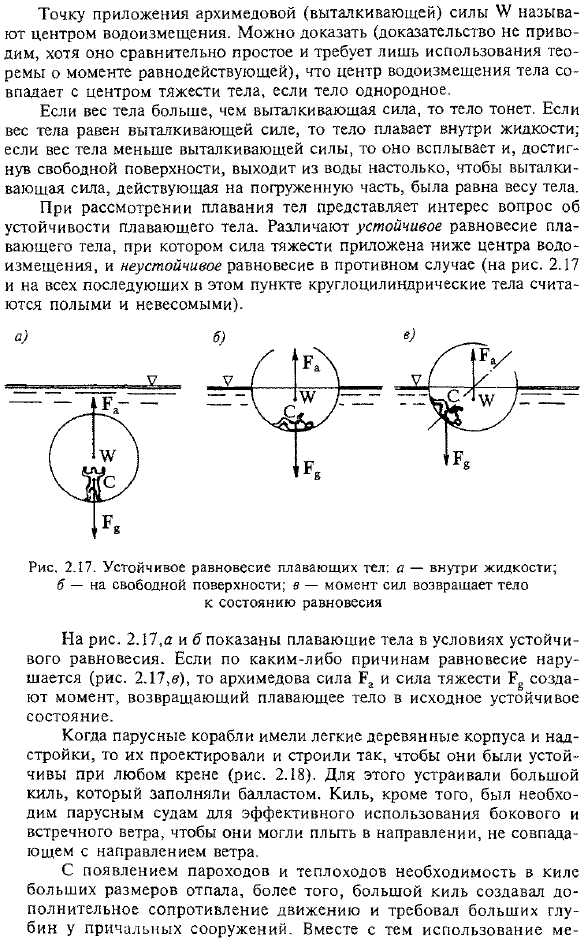
It различают устойчивое равновесие плавающего тела, в котором гравитация приложена ниже центра смещения, и в противном случае неустойчивое равновесие(на рисунке 2.17 и всех последующих в этом пункте цилиндрах считается полым и невесомым). На рис. 2.17, а и в показано плавающее тело в устойчивом равновесии. Если равновесие нарушается по какой-либо причине (рис.2.17, в), силы Архимеда Ra и гравитация P2 создают моменты, возвращающие плавающее тело в исходное устойчивое состояние. Когда парусные суда имели легкий деревянный корпус и надстройку, они были спроектированы и построены так, чтобы быть устойчивыми при любом крене (рис.2.18).Для этого был установлен большой киль, заполненный балластом. placed.
Также, строго говоря, он не стабилен (центр тяжести выше центра смещения), и на небольших валках он не опрокидывается. Людмила Фирмаль
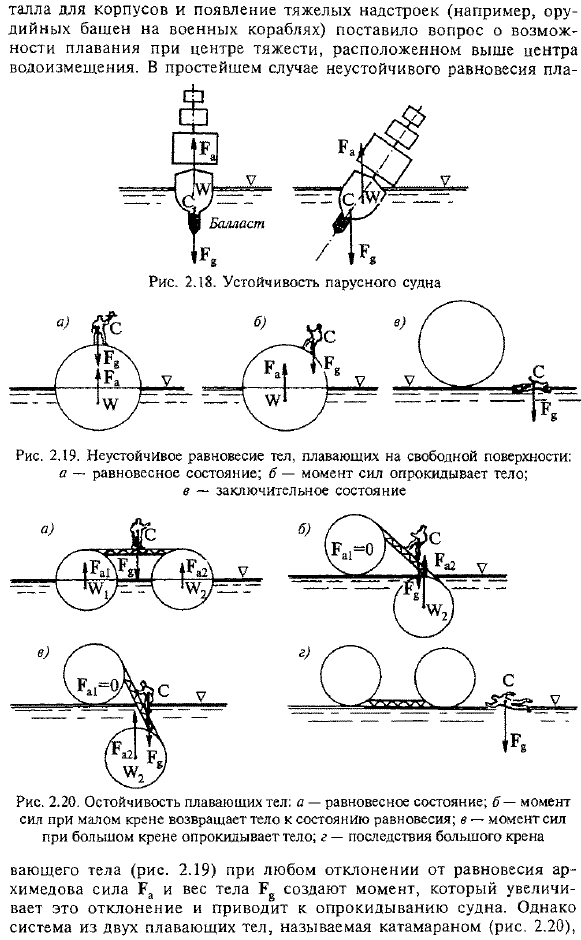
- In кроме того, киль был необходим парусным судам для эффективного использования бокового и встречного ветра, что позволяло им плыть в направлении, не совпадающем с направлением ветра. С появлением паровых и моторных судов необходимость в большом Киле отпала, а еще большие Кили создавали дополнительное сопротивление движению, что требовало большой глубины в причальных сооружениях. Однако、 Сорок шесть С появлением корпусных талеров и тяжелых надстроек (например, башенок военных кораблей) встал вопрос о возможности плавания в центре тяжести выше центра водоизмещения.
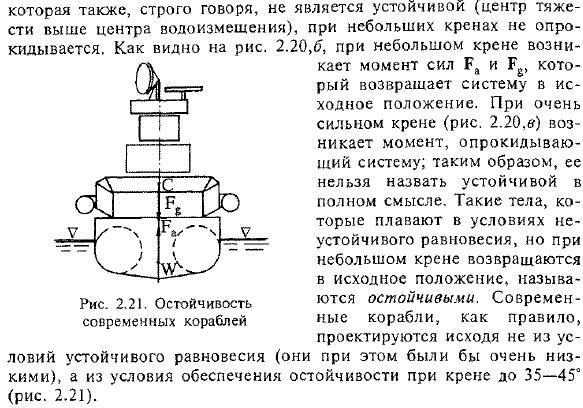
Простейший случай неустойчивого равновесия 2.19) если имеет место отклонение от равновесного состояния, то момент вызван силой Ra и весом Архимеда, и это отклонение становится большим, приводя к опрокидыванию сосуда. Однако система из 2 плавающих тел, называемая катамараном(рис. 2.20)、 Сорок семь As как показано на рис. 2.20.6, при малом крене возникают силы Ra и P, и система возвращается в исходное положение. При очень сильных кренах (рис. 2.20, в)происходит момент переворачивания системы. Поэтому его нельзя назвать устойчивым в полном смысле этого слова.
Смотрите также:
Примеры решения задач по гидравлике
Возможно эти страницы вам будут полезны:
1.Нормальные напряжения в стенках круглоцилиндрической трубы (котельная формула).
2.Структура общих формул для вычисления.

