Заказать математическое программирование — решение на заказ онлайн

Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Как заказать выполнение заданий по математическому программированию

Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.

Сколько может стоить заказ математического программирования

Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения заказа

Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить заказ

Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Гарантии и исправление ошибок

В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.

Чуть ниже я предоставила примеры оформления заказов по некоторым темам математического программирования, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.

На данной странице рассматриваются заказы математического программирования, постоянно встречающиеся в экономической практике. Заказы математического программирования содержат, как правило, много переменных и ограничений и не допускают решений в виде формул. Решения могут быть получены только путем итераций, работа по реализаций которых может выполняться или вручную, или, чаще всего, на ЭВМ.

Возможно эта страница вам будет полезна:

Предмет математическое программирование

В первом примере рассматривается экономико-производственная задача, для которой строится математическая модель и приведен пример ее решения симплекс-методом и двойственным симплекс-методом.

Во втором примере оригинальный простой алгоритм решения транспортной задачи в сетевой постановке, позволяющий получить оптимальное распределение продукта с указанием объемов и маршрутов поставки даже в случае, когда ограничения задачи являются несовместными, приведен алгоритм и рассмотрен пример решения задачи о максимальном потоке, не связанным с графическим представлением сети.

Решение заказов математического программирования

Для решения конкретной прикладной задачи строится математическая модель, а именно: определяются целевая функция (критерий оптимальности) и система ограничений, которые являются линейными функциями относительно выбранных переменных. В системе ограничений могут быть неравенства вида 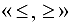и равенства. Для решения задачи полученная математическая модель приводится к каноническому виду, к левой части ограничений вида 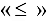добавляются неотрицательные дополнительные переменные, а к ограничениям вида 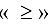— неотрицательные дополнительные переменные со знаком «-» и знак неравенства заменяется на знак равенства.

Если в полученной системе уравнений есть допустимое базисное решение (случай I: все базисные компоненты плана неотрицательны), то, исключив базисные переменные из целевой функции, если они в ней есть, полученную каноническую задачу решают симплекс-методом.

Если есть базисное решение, но оно не является допустимым (случай 2: среди базисных переменных есть отрицательные) и после исключения базисных переменных из целевой функции в 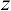-строке симплекс-таблицы нет отрицательных чисел (за исключением 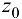), то задачу можно решать двойственным симплекс-методом.

В случае отсутствия базисного решения для использования сим-плекс-метода необходимо воспользоваться методом искусственного базиса. Заметим, что в случае 2 для решения задачи также можно воспользоваться методом искусственного базиса, так как допустимое базисное решение отсутствует.

Возможно эта страница вам будет полезна:

Решение задач по математическому программированию

Пример оформления заказа №1.

Продукция может изготавливаться па любом из трех видов оборудования. Трудоемкость и себестоимость производства центнера продукции па каждом оборудовании даны в таблице.

Сколько нужно изготовить продукции на каждом оборудовании, чтобы ее суммарная себестоимость была минимальной при условии, что трудовые ресурсы ограничены 660 п-ч, а общее количество произведенной продукции должно быть не менее 60 ц?

Решение:

Построим математическую модель задачи. Обозначим через 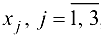, количество продукции, в центнерах, выпускаемой на 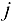-м оборудовании. Тогда целевая функция строится по суммарной себестоимости, а ограничения по трудовым ресурсам и общему количеству произведенной продукции

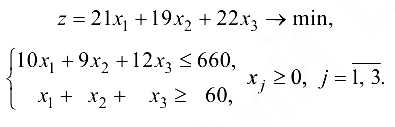
Данную задачу можно решать как симплекс-методом, так и двойственным симплекс-методом. Рассмотрим оба метода. Приведем задачу к канонической:

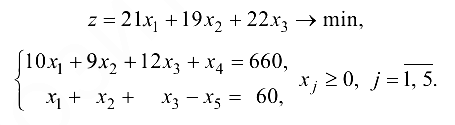
Для полученной системы уравнений существует базисное решение: свободные

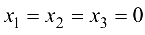
и базисные

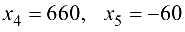
переменные.

Однако это решение не является допустимым 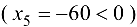, но если записать 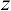-строку симплекс-таблицы для этой задачи, то она не содержит отрицательных элементов, т. е. имеет место случай 2, и задача может быть решена двойственным симплекс-методом.

Умножим второе ограничение на -1 и заполним первоначальную симплекс-таблицу.

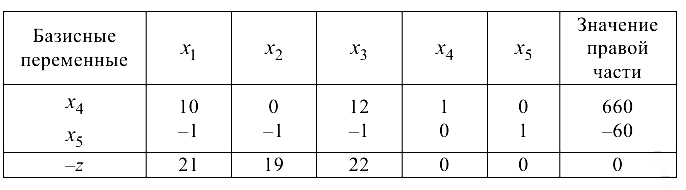
Построенный начальный базисный план не является оптимальным, так как есть отрицательные значения базисных переменных. Вторая строка является разрешающей. Подсчитаем

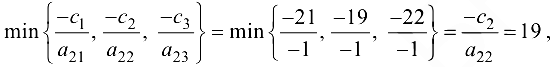
следовательно, второй столбец будет разрешающим, а элемент 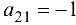— разрешающим элементом. Переменная 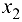вводится в базис, a 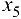— выводится.

Методом Жордана-Гаусса переходим к следующей таблице.

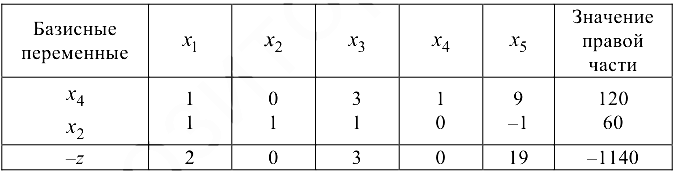
Получим оптимальный план задачи, так как все базисные переменные плана неотрицательны:

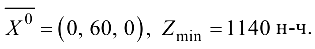
Вместе с тем для решения этой задачи можно воспользоваться методом искусственного базиса. Для этого во второе ограничение введем искусственную переменную 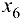и решим вспомогательную задачу минимизации искусственной целевой функции

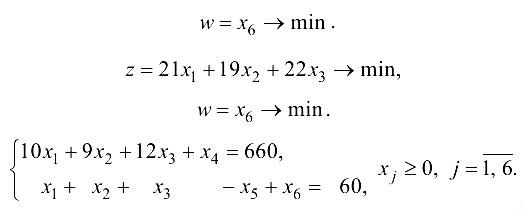
Исключаем базисную переменную 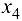из целевой функции, если она в ней есть, и искусственную базисную переменную из искусственной целевой функции. Данные шагов алгоритма будем заносить в таблицы.

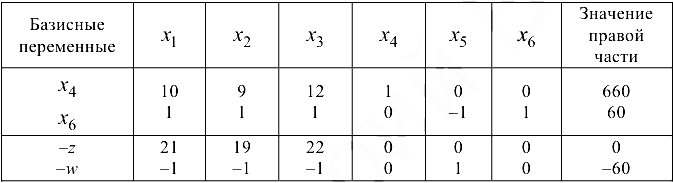
В 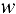-строке есть отрицательные значения, следовательно, начальный опорный план расширенной задачи не оптимален.

В качестве разрешающего столбца выберем второй и подсчитаем

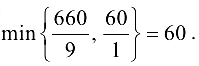
Значит, разрешающей строкой будет вторая, а разрешающим элементом 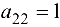. Методом Жордана-Гаусса переходим к следующей таблице.

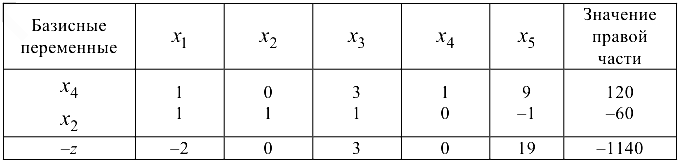
Так как искусственная переменная 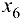ушла из базиса 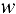=0, то первый этап решения расширенной задачи симплекс-методом завершен. Мало того, мы получили оптимальный план задачи

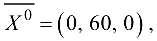
трудовые ресурсы остались неизрасходованными в количестве 120 н-ч,

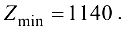
Решение заказа транспортной задачи

Транспортная задача является математической моделью широкого круга задач, которые чаще других встречаются в практических приложениях линейного программирования. Ее классическая формулировка состоит в следующем.

Имеется 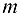источников однородного продукта или взаимозаменяемых продуктов и 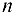пунктов его потребления (или стоков). Заданы объемы продукта 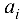у каждого источника (или его мощность) и размеры спроса 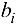(мощность) каждого стока. Известны также затраты 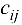, связанные с перемещением единицы продукта из источника 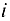в сток 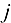. Кроме того, объем перемещаемого продукта из источника 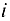в сток 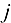не может превышать величины 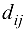(пропускной способности коммуникации). Требуется составить план перемещения продукта из источников в стоки, наиболее экономным путем обеспечивающий максимальное удовлетворение спроса всех стоков (пунктов потребления), т. е. указать объемы 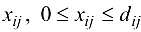, перемещаемого продукта из каждого источника 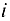в каждый сток 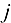, при которых общие затраты, связанные с этим перемещением, будут минимальными.

Таким образом, исходными данными для транспортной задачи являются:

векторы

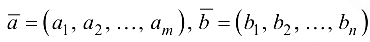
мощности источников и стоков соответственно;

матрица затрат

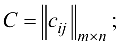
матрица пропускных способностей коммуникаций

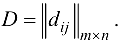
Построим математическую модель сформулированной задачи. План перемещения продукта обозначим через

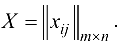
Тогда суммарные затраты , связанные с этим перемещением из всех источников во все стоки, выражаются суммой

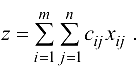
Если суммарная мощность источников

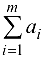
равна суммарной мощности стоков

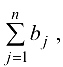
то транспортная задача называется замкнутой. Тогда условия полного удовлетворения спроса (мощности) каждого стока имеют вид

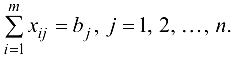
Весь продукт из каждого источника должен быть перемещен в стоки. Формально это означает, что

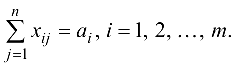
Кроме того, объемы переносимого продукта — неотрицательные числа, которые не могут превышать пропускных способностей соответствующих коммуникаций, т. е. должны выполняться условия

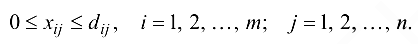
Таким образом, формально транспортная задача сводится к минимизации целевой функции (2.1), при условии, что переменные удовлетворяют ограничениям (2.2)—(2.4).

Очевидно, что для любой матрицы 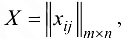удовлетворяющей условиям (2.2)-(2.4), имеют место неравенства

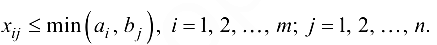
Поэтому если

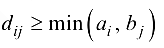
для всех

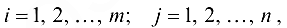
то мы имеем классическую транспортную модель. Условимся, что если

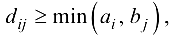
то будем считать пропускную способность этой коммуникации равной любому числу, большему чем

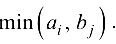
Следует отметить, что во многих прикладных задачах суммарная мощность источников может превосходить суммарную мощность стоков:

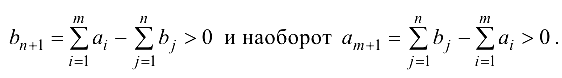
Такая задача называется открытой транспортной моделью. Открытую модель можно свести к замкнутой.

В первом случае вводится фиктивный сток 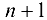с мощностью 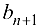. Размеры остатка продукта 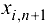у каждого источника 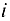можно регулировать в зависимости от введенного штрафа за единицу оставшегося у 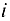-го источника продукта. Часто полагают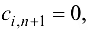 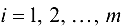. Пропускные способности 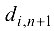, коммуникаций, ведущих в фиктивный сток, пе ограничены, т. е. равны любому числу, большему чем

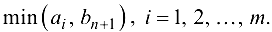
Во втором случае вводится фиктивный источник 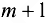с мощностью 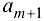. Размер неудовлетворенной мощности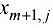 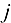-го стока может регулироваться величиной ущерба 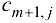. Если ущерб для всех стоков одинаков, то полагают

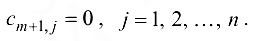
Пропускные способности

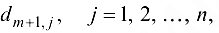
не ограничены, т.е. равны любому числу, большему чем величина 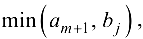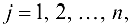соответственно.

В силу вышесказанного в дальнейшем будем рассматривать замкнутую транспортную модель, т. е. полагая, что

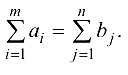
В случае когда ограничения на пропускные способности отсутствуют (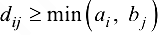 для любых 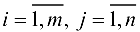), задача решается методом потенциалов. В противном случае можно использовать его модификацию, однако она неудобна для программной реализации, и даже на стадии построения первоначального опорного плана требуется использование метода искусственного базиса. Поэтому для ее решения целесообразным является использование двойственного метода, основанного на сетевой постановке задачи.

Вначале рассмотрим транспортную задачу без ограничений на пропускные способности коммуникаций (классическую транспортную задачу) с вектором мощностей источников 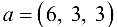, стоков 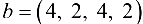и матрицей

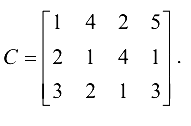
Процесс решения начинается с предварительного этапа — построения первоначального опорного плана методом «северозападного угла» или методом минимального элемента, который использован в данном примере.

Цифры, стоящие в скобках около строк и столбцов матрицы 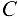, обозначают номер шага, на котором соответствующие строки и столбцы вычеркиваются. Цифры в скобках над элементами матрицы 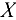обозначают номер шага, на котором определяются ее соответствующие элементы, а над столбцами вектора 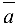и около строк вектора 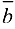— номера шагов, на которых они принимают указанные значения. Поскольку после 6-го шага в первой строке нет ни одного иевычеркнутого элемента, она может быть вычеркнута (правило вычеркивания). То есть положительные компоненты матрицы 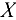не образуют цикл, их число равно 6 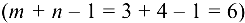. Таким образом, в результате предварительного этапа получен исходный опорный план транспортной задачи, множество базисных компонент

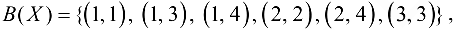
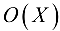— все остальные компоненты плана .

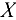Итерация 1. Определяем потенциалы, отвечающие исходному опорному плану путем решения системы уравнений

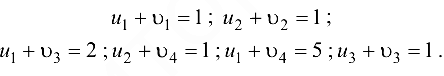
Полагая 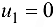, последовательно вычисляем и,

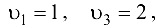
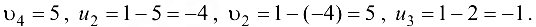
Вычисляем величины

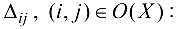
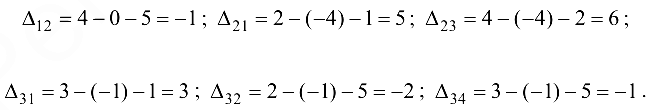
План не является оптимальным, так как

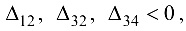
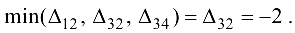
Улучшение плана осуществляется за счет увеличения компоненты —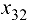, добавление ее к базисным компонентам порождает единственный цикл

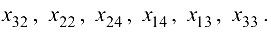
Определяем

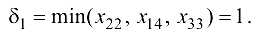
Увеличиваем нечетные компоненты цикла (помеченные знаком «+») и уменьшаем четные (помеченные знаком «-») на величину 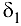= 1 и получаем новый опорный план (пустые клетки соответствуют нулевым компонентам плана).

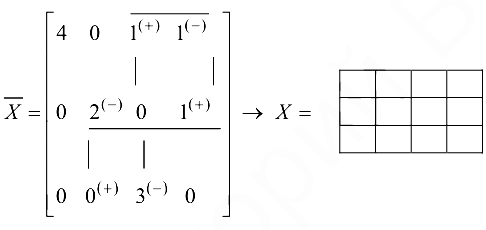
Итерация 2. Множество базисных компонент

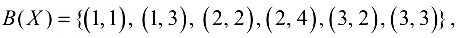
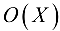— все остальные компоненты плана.

Определяем потенциалы для полученного опорного плана:

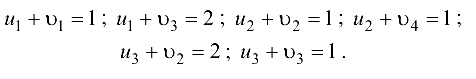
Полагая 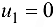последовательно вычисляем

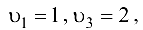
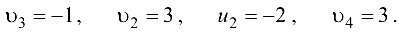
Вычисляем величины

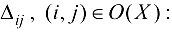
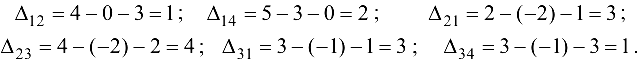
Поскольку все величины неотрицательны, то план является решением нашей задачи.

Рассмотрим теперь общую транспортную задачу с ограниченными пропускными способностями в сетевой постановке.

На плоскости отмечаются (кружками) источники (с номерами 1, 2, …, 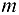) и стоки (с номерами 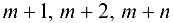), а также отмечаются фиктивный источник и сток с номерами 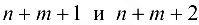соответственно (рисунок).

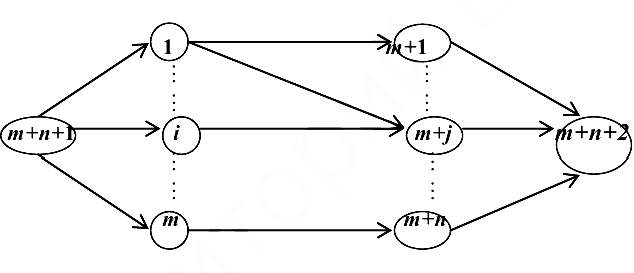
Если принять пропускную способность коммуникации 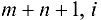, равной 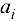, коммуникации 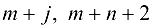, равной 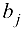, а стоимости переноса по ним единицы продукта, равными 0, то задача может быть сформулирована следующим образом: построить максимальный поток продукта из фиктивного источника 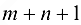в фиктивный сток 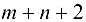, стоимость которого минимальна. Понятно, что величина потока 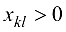по любой коммуникации 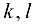не может превышать ее пропускной способности 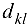. Суммарный объем продукта, перемещаемого из каждого источника 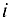, равен величине продукта, перемещаемого в 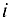из фиктивного источника 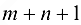, а суммарный объем продукта, перемещаемого в каждый сток 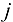, равен величине продукта, перемещаемого из 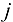в фиктивный сток .

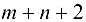Введем в рассмотрение векторы модифицированных мощностей

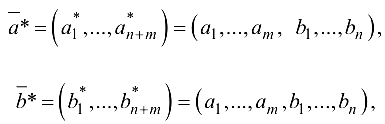
матрицы модифицированных стоимостей

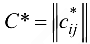
и пропускных способностей

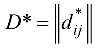
порядка

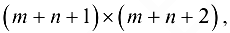
определенных следующим образом:

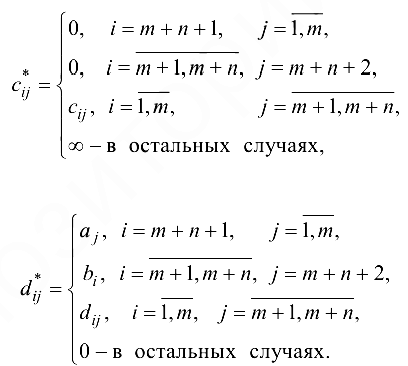
Опишем алгоритм решения транспортной задачи. Не уменьшая общности, предположим, что 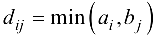, если 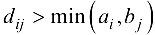для всех .

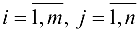Общая итерация. Осуществляем тернарные операции над элементами матрицы модифицированных стоимостей

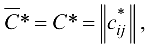
последовательно по всем

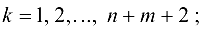
полагая

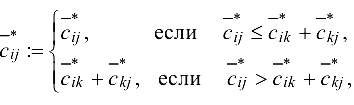
для всех

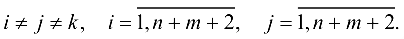
Одновременно с выполнением операций (2.5) изменяем элементы вспомогательной матрицы 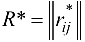порядка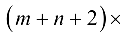 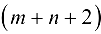(первоначально полагаем ):

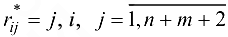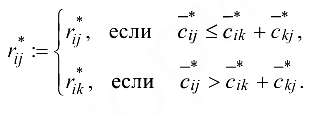
Если

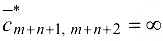
задача решена. В противном случае с помощью вспомогательной матрицы 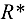определяем множество индексов

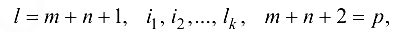
где

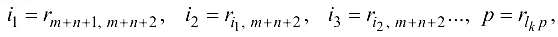
и множество

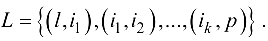
Находим

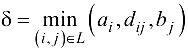
и вычисляем:

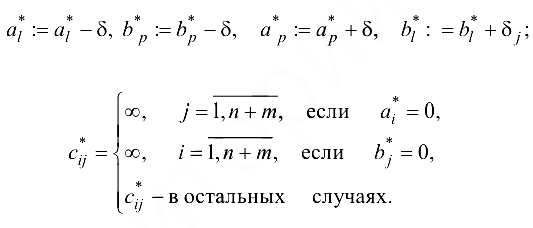
Переходим к общей итерации.

После окончания работы алгоритма находим матрицу

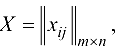
где

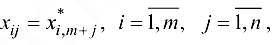
которая является решением задачи.

Если одно из ограничений не выполнено, то это означает, что исходная задача не имеет допустимых решений.

Тем не менее полученный план является оптимальным планом перемещения максимально возможного количества продукта из источников в стоки при данных ограничениях.

Проиллюстрируем работу алгоритма на рассмотренном выше примере:

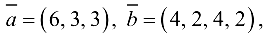
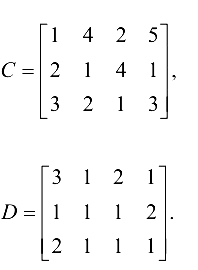
Формируем матрицы модифицированных стоимостей и пропускных способностей:

Прочерки вместо элементов матрицы означают сколь угодно большое число (оо).

После осуществления общей итерации получим

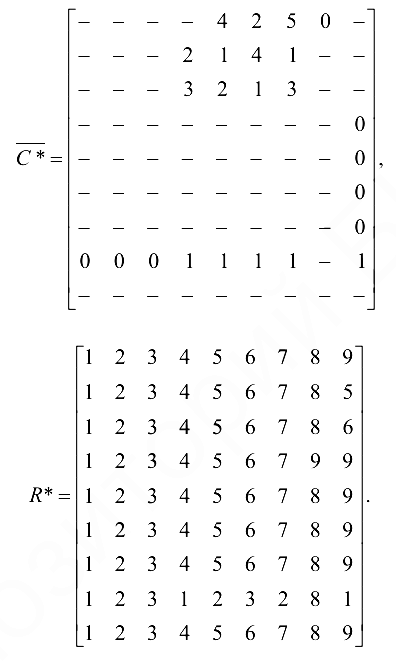
Так как

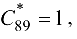
с помощью матрицы 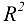находим

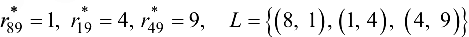
и изменяем матрицы

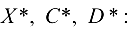
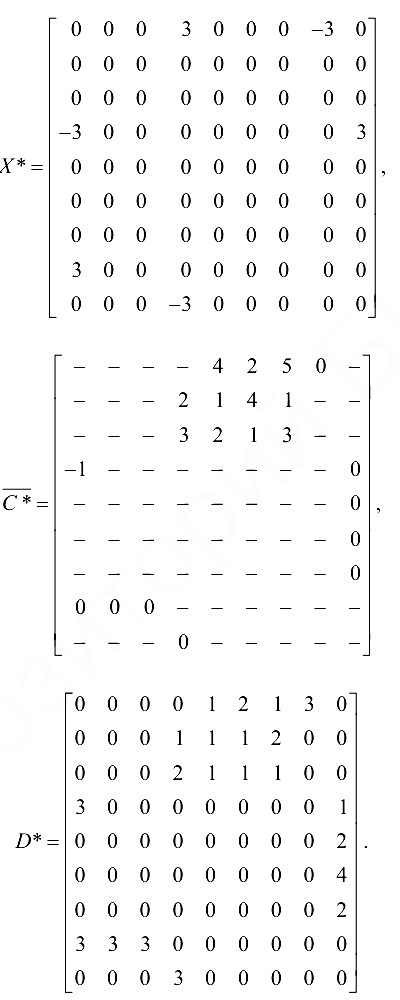
После осуществления над этими матрицами еще семи операций получаем матрицы :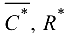

Так как 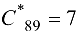, с помощью матрицы 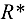определяем множество индексов

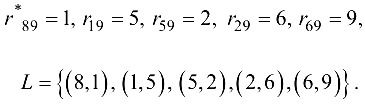
Находим 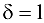и вычисляем

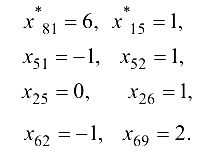
Новые матрицы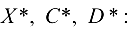

После осуществления тернарных операций над матрицей 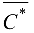получим 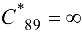, т. е. задача решена, оптимальное решение

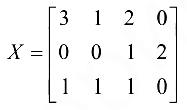
при значении целевой функции .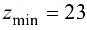

Пример оформления заказа №2.

Тернарной операцией над матрицей 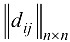по индексу 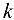называется операция

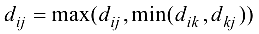
для всех .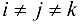

Рассмотрим вспомогательную матрицу 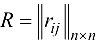, элементы которой 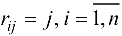. Одновременно с выполнением тернарной операции элементы матрицы 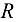изменяются по следующему правилу:

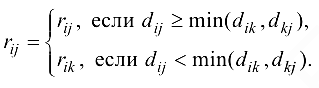
Эти операции являются основой метода построения максимального потока в многополюсной сети. Опишем алгоритм решения задачи.

Подготовительный этап. Для начальной потоковой матрицы 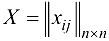(как правило, на начало работы алгоритма 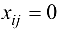для всех 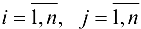) формируем модифицированную матрицу пропускных способностей 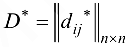, полагая

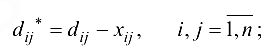
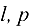— индексы источника и стока соответственно.

Общая итерация. Осуществляем тернарные операции над матрицей

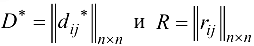
последовательно по всем индексам

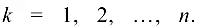
Если в полученной в результате матрице

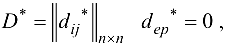
алгоритм заканчивает работу. В противном случае переходим к шагу 1.

Шаг 1.

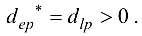
С помощью вспомогательной матрицы

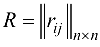
находим путь

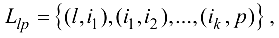
вдоль которого можно увеличить поток на максимально возможную величину 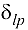. Здесь

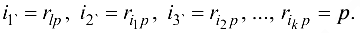
Далее полагаем

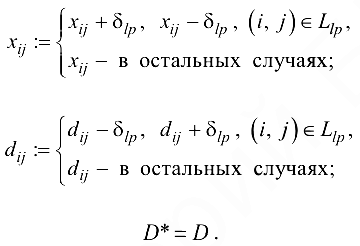
Переходим к общей итерации. Проиллюстрируем работу алгоритма на следующем примере.

Возможно эта страница вам будет полезна:

Примеры решения задач по математическому программированию

Пример оформления заказа №3.

Найти максимальный поток из вершины 1 в вершину 7 в сети, заданной матрицей пропускных способностей дуг

Решение:

Полагаем

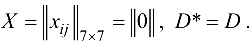
Итерация 1. Получаем

Так как 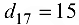, с помощью матрицы 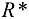находим увеличивающий путь:

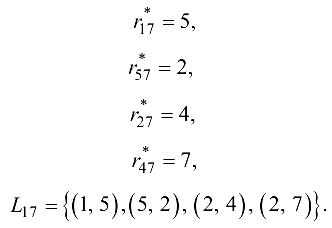
Находим матрицы:

Итерация 2.

Находим матрицы:

Итерация 3.

Находим матрицы

Итерация 4.

Находим матрицы:

Итерация 5.

Алгоритм закончил работу. Потоковая матрица

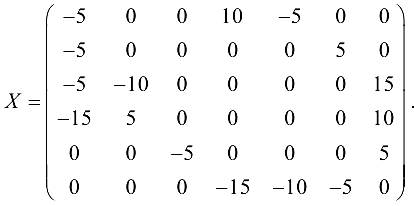
Если элемент 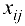матрицы 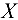отрицателен, то это означает, что поток величины 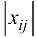переносится из вершины 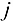в вершину .

Возможно эти страницы вам будут полезны:

Помощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа линейное программированиеЛинейное программирование в ExcelКурсовая работа по линейному программированию