Курсовая работа по линейному программированию

Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Линейное программирование

Линейное программирование — наиболее разработанный и широко применяемый раздел математического программирования. Это объясняется следующим:

• математические модели очень большого числа экономических задач линейны относительно искомых переменных;
• эти типы задач в настоящее время наиболее изучены;
• для них разработаны специальные конечные методы, с помощью которых эти задачи решаются, и соответствующие стандартные программы для их решения на ЭВМ;
• многие задачи линейного программирования, будучи решенными, нашли уже сейчас широкое практическое применение в народном хозяйстве;
• некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.

Задача линейного программирования

Для производства двух видов издели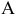й и 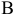используются три типа технологического оборудования.

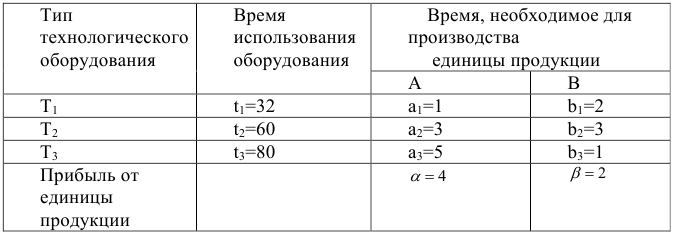
Для производства единицы изделия 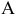оборудование первого типа используется 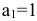час, оборудование второго типа — 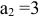часа, оборудование третьего типа — 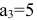часов. Для производства единицы изделия В оборудование первого типа используется 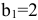часа, оборудование второго типа — 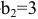часа, оборудование третьего типа — 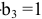час. На изготовление всех изделий предприятие может использовать оборудование первого типа не более, чем 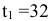часа, второго типа не более, чем 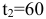часов, третьего типа не более, чем 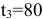часов. Прибыль от реализации готового изделия 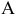составляет 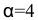денежные единицы, а изделия 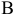составляет 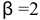денежные единицы. Составить план производства издели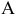й и 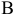, обеспечивающий максимальную прибыль от их реализации. Дать геометрическое решение задачи. Решить задачу симплексным методом путем преобразования симплекс-таблиц.

Решение:

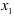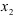Обозначим через и количество изделий соответственно 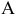и 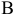, запланированных к производству.

Для производства издели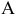й и :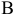

оборудование первого типа используется 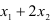(часов),
оборудование второго типа используется 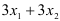(часов),
оборудование третьего типа используется 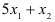(часов).

На изготовление всех изделий предприятие может использовать оборудование первого типа не более, чем 32 часа, второго типа — не более, чем 60 часов, третьего типа не более, чем 80 часов. Эти ограничения запишем в виде системы неравенств:

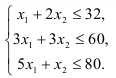
По смыслу задачи 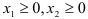. Прибыль от реализации изделий 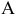составит 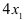(денежных единиц), изделий 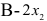(денежных единиц). Общая прибыль от реализации издели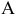й и 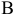составит .

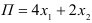Приходим к математической модели поставленной задачи: составить план производства изделий 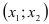, удовлетворяющий системе ограничений 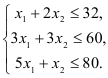и условию 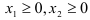, при котором функция 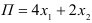, принимает максимальное значение.

Возможно эта страница вам будет полезна:

Предмет математическое программирование

1-й способ решения (графический метод)

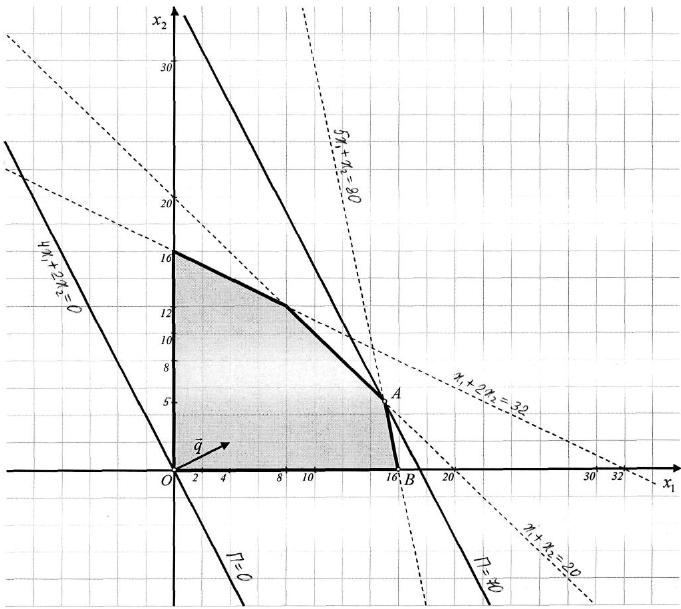
Решим полученную задачу сначала графически. Дадим геометрическое толкование задачи. Построим область допустимых решений из системы ограничений, находя последовательно множество решений каждого из неравенств.

Неравенство 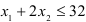задаёт полуплоскость, ограниченную сверху прямой 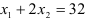. Прямая 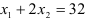проходит через точки (0; 16) и (32;0). Неравенство 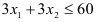задаёт полуплоскость, ограниченную сверху прямой 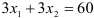, то есть прямой 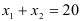. Прямая 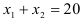проходит через точки (0;20) и (20;0). ). Неравенство 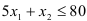задаёт полуплоскость, ограниченную сверху прямой 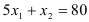. Прямая 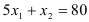проходит через точки (16;0) и (10;30). Неравенства 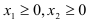ограничивают множество допустимых решений 1-ой координатной четвертью. Строим опорную прямую 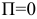, то есть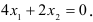

В направлении вектора 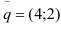целевая функция 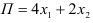, растёт, а в направлении, противоположном вектору 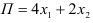— убывает. Найдём точку 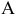пересечения прямой, параллельной опорной прямой, и самой удалённой от неё в направлении роста целевой функции точкой из области допустимых решений.

Точка 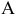— точка пересечения прямых 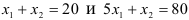. Координаты точки 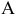найдём, решив систему уравнений:

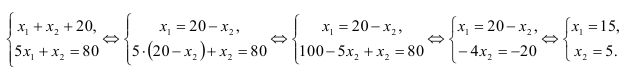
Итак, точка А(15;5).

Таким образом, максимум линейной функции

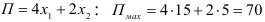
(денежных единиц) при оптимальном решении

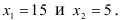
Следовательно, наибольшая прибыль от реализации изделий — 70 денежных единиц будет при производстве 15 изделий 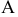и 5 изделий .

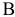Возможно эта страница вам будет полезна:

Решение задач по математическому программированию

2-ой способ решения (симплексным методом)

Представим задачу в виде основной задачи линейного программирования:

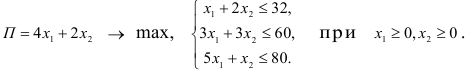
С помощью дополнительных неотрицательных переменных перейдём к системе уравнений. Введём новые переменные 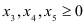и добавим их к левым частям ограничений. Получим систему уравнений вместо системы неравенств.

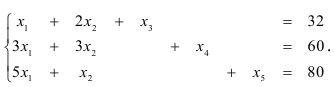
Функция цели имеет вид:

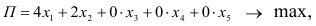
Запишем эту систему уравнений в виде:

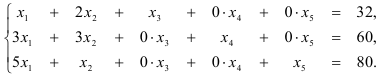
Запишем теперь эту систему ограничений в форме векторного уравнения:

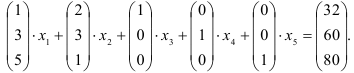
Введём векторы:

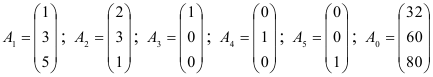
Так как среди векторов есть три единичных 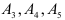, то выбираем их в качестве базисных. Неизвестные переменные 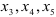являются базисными, а переменные 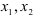-свободными неизвестными, которые приравниваем нулю.

Получим систему:

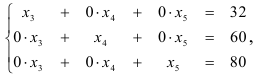
из которой следует

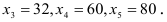
Итак, получаем первоначальный опорный план;

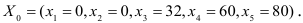
Для проверки плана на оптимальность составим симплексную таблицу, которая имеет общий вид:

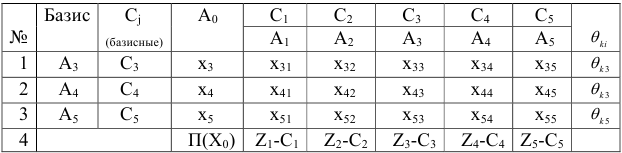
В этой таблице записаны координаты векторов 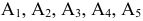в базисе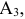 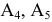, то есть разложение всех векторов 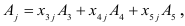, где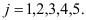

Критерий оптимальности плана: если для некоторого плана 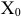разложения всех векторов 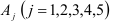в данном базисе удовлетворяют условию 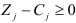, то план 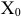является оптимальным и доставляет линейной функции максимальное значение. При невыполнении условия оптимальности в базис включают в первую очередь тот вектор, которому соответствует 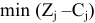, где минимум берется по тем 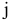, для которых 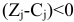. Первая симплексная таблица имеет вид:

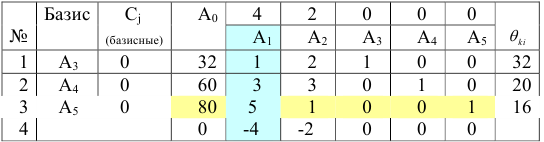
Поясним вычисления последней строки и последнего столбца.

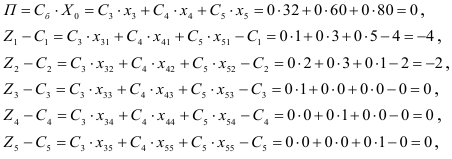
Для векторов базиса 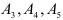оценки 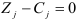. Среди оценок имеются две отрицательные:

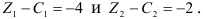
Это означает, что первоначальный опорный план не является оптимальным, и его необходимо улучшить.

Базис нового плана будет содержать два вектора старого плана и новый вектор 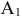, которому соответствует 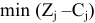. Столбец , соответствующий вектору 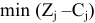, является разрешающим (ведущим ).

Для того, чтобы определить какой вектор нужно исключить из первоначального базиса, подсчитаем отношения координат 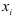исходного плана соответственно к элементам 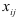разрешающего столбца, то есть 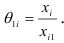Для координат вектора :

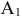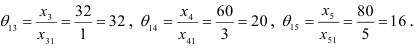
Выбираем 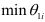, что соответствует третьей строке, следовательно, из базиса исключаем вектор 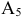. Новый базис состоит из векторов 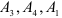. Третья строка является разрешающей. Элемент 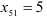, стоящий на пересечении разрешающей строки и разрешающего столбца, называется разрешающим.

Найдём коэффициенты разложения всех векторов в новом базисе. Поставленная задача решается просто. Разрешающий элемент 5 стоит на пересечении третьей строки и столбца 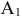. Подсчитаем новые элементы третьей строки. Для этого старые элементы этой строки (№3) разделим на разрешающий элемент 5 и запишем в строчку с номером 7 второй симплексной таблицы. Так как вектор 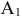входит в базис, то его координаты кроме одной сделаем нулевыми. Для этого из всех элементов строки №1 вычтем соответствующие элементы строки №7 и результат запишем в строку №5. Затем все элементы строки №7 умноженные на 3 вычтем соответственно из элементов строки №2 и результат запишем в строку №6

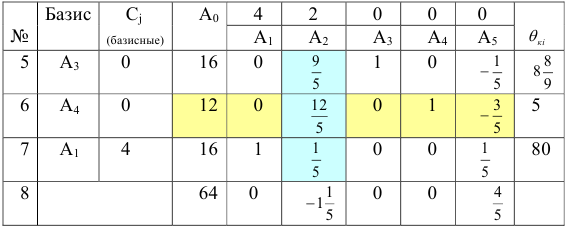
Итак, получили новый опорный план:

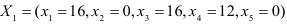
и новое разложение векторов

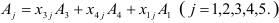
в базисе

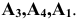
Вторая симплексная таблица в условных обозначениях имеет вид:

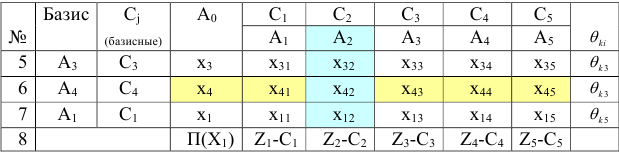
Для проверки плана на оптимальность вычисляем элементы строки №8:

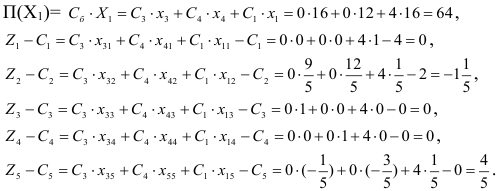
Оценочная строка №8 второй симплексной таблицы содержит один отрицательный элемент. Критерий оптимальности не выполнен. Столбец 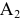является разрешающим. Для того, чтобы определить какой вектор нужно исключить из базиса 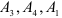, подсчитаем отношения координат 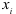к элементам 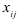разрешающего столбца 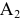, то есть

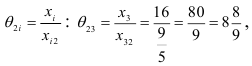
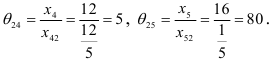
Выбираем 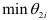, что соответствует строке №6, которая является разрешающей. Из базиса исключаем вектор 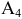, вместо него вводим вектор 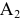. Новый базис состоит из векторов 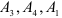. Элемент

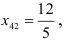
стоящий на пересечении разрешающей строки и разрешающего

столбца, является разрешающим. Новый опорный план имеет вид:

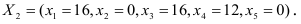
Аналогично как в прошлый раз, строим третью симплексную таблицу. Все элементы строки №6 делим на разрешающий элемент 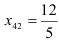и записываем в строку №10. Все координаты вектора 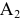, кроме одного, должны обратится в нуль. Для этого все элементы строки №10 умножим на 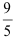и вычтем из соответствующих элементов строки №5, результат запишем в строку №9. Затем все элементы строки №10 умножим на 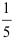и вычтем из соответствующих элементов строки №7, результат запишем в строку №11.

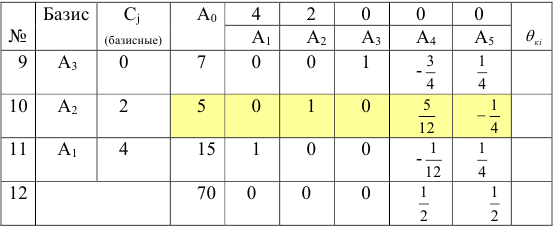
Вычислим элементы строки №12:

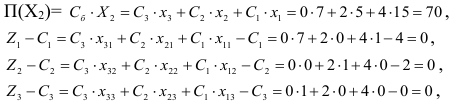
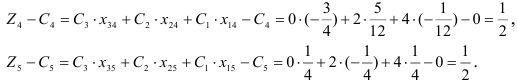
Оценочная строка №12 не содержит отрицательных элементов. Критерий оптимальности выполнен. Значит,

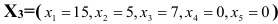
оптимальное базисное решение, при котором функция цели

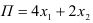
принимает максимальное значение. Переменные 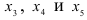не входят в исходную задачу, Следовательно,

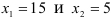
решение задачи; наибольшая прибыль

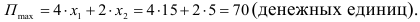
Ответ: план производства издели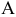й и 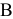таков: наибольшая прибыль от реализации изделий — 70 денежных единиц будет при производстве 15 изделий 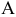и 5 изделий .

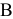Возможно эта страница вам будет полезна:

Примеры решения задач по математическому программированию

Транспортная задача

Имеются четыре пункта отправления 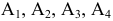однородного груза и пять пунктов 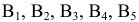его назначения. На пунктах 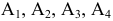груз находится в количестве 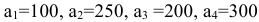тонн соответственно. В пункты 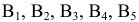требуется доставить соответственно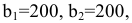 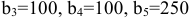тонн груза.

Расстояния в сотнях километров между пунктами отправления и назначения 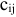приведены в соответствующих клетках таблицы.

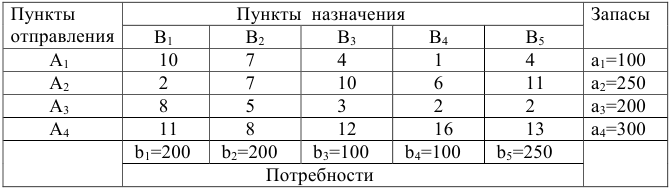
Найти такой план перевозок, при котором общие затраты на перевозку грузов будут минимальными.

Указания: 1) считать стоимость перевозок пропорциональной количеству груза и расстоянию, на которое груз перевозится; 2) для решения задачи использовать методы: 1) северо-западного угла, 2) минимальной стоимости и 3) потенциалов.

Возможно эта страница вам будет полезна:

Заказать работу по математическому программированию

Решение:

1-ый способ решения (метод северо-западного угла)

Не учитывая стоимости перевозки, начинаем удовлетворение потребностей первого потребителя 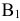за счет запаса поставщика 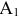. Для этого сравниваем 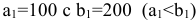. Запас 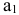полностью выбираем ( в левый угол клетки 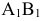записываем 100). Остальная потребность 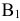выбирается из запаса второго поставщика 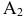( в левый угол клетки 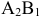записываем 100). Потребность 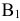удовлетворена. Теперь удовлетворяем потребности 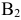. Ему нужно 200 тонн груза, а у поставщика 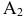осталось 150. Выбираем этот груз потребителю 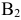, недостающие 50 тонн груза выбираем у поставщика 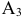и т. д. Процесс продолжаем до тех пор пока не удовлетворим всех потребителей.

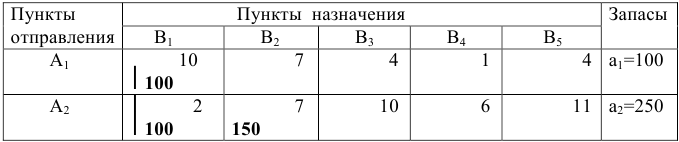
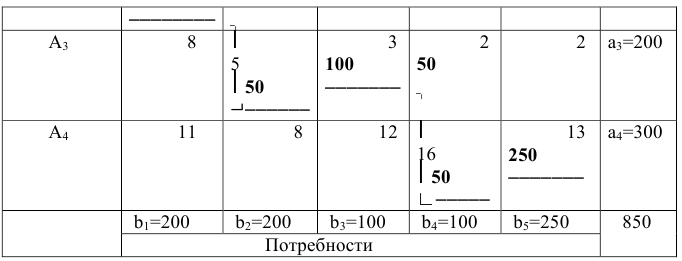
Как следует из таблицы распределение груза производится из левого верхнего угла и следует в правый нижний угол, видимо поэтому, такой процесс называется методом северо-западного угла.

При построении этого плана стоимость перевозок не учитывалась, поэтому построенный план далёк от оптимального.

Найдём общую стоимость составленного плана как сумму произведений объёмов перевозок на соответствующие стоимости в этих же клетках:

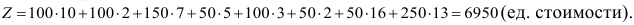
Ответ: план представлен таблицей, общая стоимость всех перевозок 6950(ед.стоимости).

Возможно эта страница вам будет полезна:

Помощь по математическому программированию

2-ой способ решения (метод минимальной стоимости)

Суть метода состоит в том, что из всей таблицы стоимостей выбирают наименьшую и в эту клетку помещают меньшее из чисел 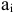или .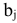

Затем из рассмотрения исключают либо строку (если запасы 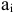выбраны), либо столбец (если потребитель 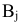полностью удовлетворён). Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжается таким же образом, пока все запасы будут распределены.

Сначала выбрали клетку 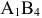(из рассмотрения исключается первая строка), затем клетку 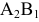( из рассмотрения исключается первый столбец), потом клетку 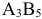(из рассмотрения исключается третья строка). В оставшихся строчках (второй и четвёртой) распределяем груз так, чтобы удовлетворить оставшихся потребителей.

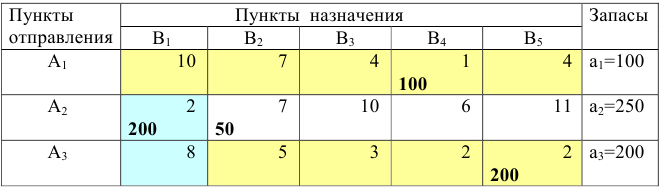
Найдём общую стоимость составленного плана как сумму произведений объёмов перевозок на соответствующие стоимости в этих же клетках:

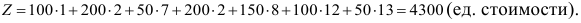
Ответ: план представлен таблицей, общая стоимость всех перевозок 4300(ед.стоимости).

Возможно эта страница вам будет полезна:

Задачи математического программирования

3-ий способ решения (метод потенциалов)

В качестве первоначального плана возьмём план, полученный методом минимальной стоимости

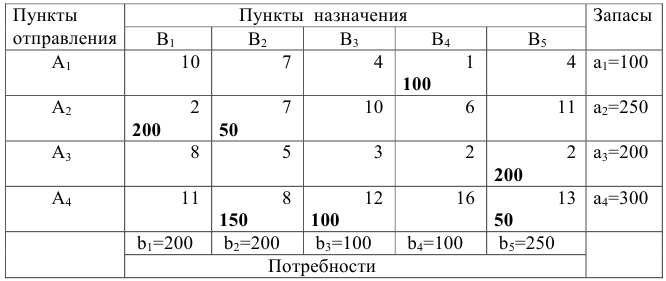
Критерий оптимальности. Чтобы план был оптимальным, необходимо выполнение следующих условий:

а) для каждой занятой клетки сумма потенциалов должна быть равна стоимости 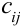единицы перевозки груза, стоящей в этой клетке

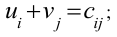
б) для каждой незанятой клетки сумма потенциалов должна быть не больше стоимости 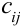единицы перевозки груза, стоящей в этой клетке

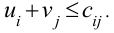
Если хотя бы одна незанятая клетка не удовлетворяет последнему условию, то опорный план не является оптимальным, и его можно улучшить.

Таким образом, для проверки плана на оптимальность необходимо построить систему потенциалов.

Возможно эта страница вам будет полезна:

Задача линейного программирования

Построение системы потенциалов для плана

Для построения системы потенциалов используем условие 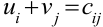, для каждой занятой клетки. Систему потенциалов можно построить для невырожденного опорного плана, который содержит 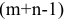занятых клеток, где 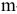-число поставщиков, 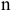-число потребителей. Для каждой занятой клетки можно составить уравнение

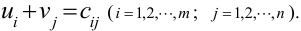
Таких уравнений будет 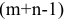, а неизвестных .

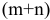Уравнений на одно меньше, чем число неизвестных, поэтому система имеет бесчисленное множество решений и одному неизвестному придают произвольное значение (обычно нулевое). После этого определяются остальные потенциалы.

В таблице 7 занятых клеток

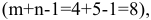
поэтому план вырожденный. Выбираем строку, в которой имеется наибольшее число занятых клеток. Такая строка 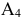, поэтому полагаем в этой строке потенциал 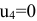. Клетка 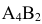содержит стоимость 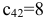, для неё должно выполняться условие 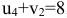, откуда следует потенциал 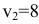. Далее клетка 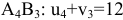, откуда 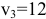. Следующая клетка по этой строке 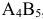, в которой 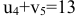, с учето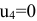м имеем 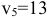. В клетке 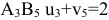или 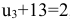, отсюда 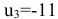. Для следующей клетки 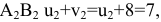поэтому 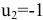. В клетке 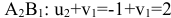, следовательно, потенциал .

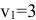Потенциалы 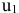и 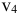остались неопределёнными, это произошло потому, что опорный план вырожденный. Введем клетку с нулевыми перевозками, которую будем называть фиктивно занятой. Фиктивно занятую клетку надо сделать в строке 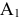или в столбце 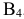. Задача решается на минимизацию, поэтому целесообразно взять клетку с наименьшей стоимостью 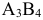(см. следующую таблицу).

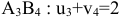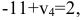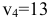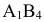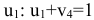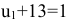В этой клетке или , значит, . Далее из клетки находим или , отсюда 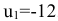. Система потенциалов построена.

2) Проверка выполнения условия оптимальности:

Для каждой незанятой клетки проверяем выполнение условия

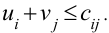
Если для всех незанятых клеток выполняется это условие, то план

оптимальный. Если для некоторых клеток и

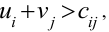
то план не является оптимальным. Тогда для этих клеток находим величину разности

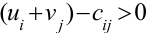
и записываем в нижний левый угол этой клетки.

Это клетки

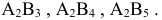
Таким образом, имеются три клетки, в которых нарушено условие оптимальности; разности соответственно равны 1,6 и 1.

3) Выбор клетки, в которую необходимо послать перевозку:

В задаче линейного программирования в базис включается тот вектор, которому соответствует 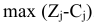. Если отождествлять занятые клетки с векторами, составляющими базис; а незанятые клетки — с остальными векторами системы ограничений и если отождествлять 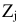суммой 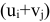, то в транспортной задаче загрузке подлежит клетка, которой соответствует 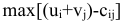. Поэтому клетку 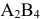необходимо сделать занятой.

4) Построение цикла и определение величины перераспределения:

Отмечаем знаком (+) незанятую клетку 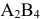. До этого в таблице было 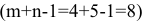занятых клеток, которые составляли базис. Теперь в таблице стало 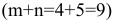занятых клеток (линейно зависимых), поэтому должен существовать замкнутый цикл. Намечаем его пунктиром, поочерёдно расставляем знаки (+) и (-) на поворотах, начиная с клетки .

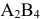Затем находим 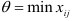, где 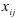— перевозки, стоящие в вершинах цикла, отмеченные знаком (-). Величина 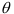определяет количество груза, которое надо перераспределить по циклу. Величина 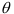прибавляется к перевозкам, отмеченным знаком (+), и вычитается от перевозок, отмеченным знаком (-). Имеем в 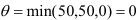. Следовательно, нулевую перевозку перемещаем в клетку 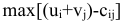, остальные не изменяются.

В результате получен новый опорный план, который снова подлежит проверке на оптимальность.

5) Изменение системы потенциалов:

Для клетки 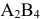должно выполняться условие

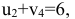
на самом деле

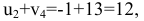
следовательно, потенциалы нужно уменьшать. Лучше уменьшить 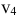на 6. Надо теперь переоценить потенциалы в клетке 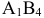. Имеем 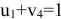или 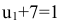, откуда следует 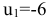( см. следующую таблицу).

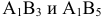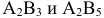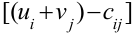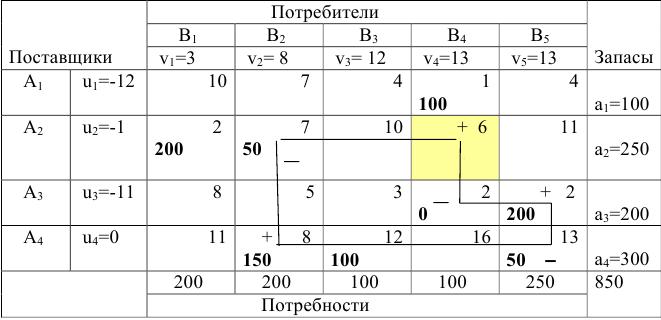
Проверяем на оптимальность незанятые клетки. В первой строке клетки , во второй строке клетки не удовлетворяют условию оптимальности; находим для них величины разностей и записываем в нижние левые углы этих клеток. Максимум разности находится в клетке 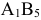, поэтому эта клетка подлежит загрузке; отмечаем эту клетку знаком (+) и строим цикл ( см. следующую таблицу)

Затем находим по клеткам, отмеченным знаком (-), величину #=min (100;50;50)=50. Перераспределяем перевозки: прибавляем 50 единиц груза в клетки со знаком (+) и вычитаем такой же груз из клеток со знаком (-). Получим следующую таблицу

В полученном опорном плане изменяем систему потенциалов. У нас появилась новая клетка с грузом 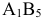.Чтобы выполнялось условие 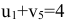, лучше уменьшить потенциал 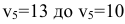, оставив неизменным потенциал 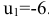. В последнем столбце 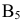есть ещё одна клетка с грузом 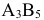, в которой должно выполняться условие 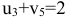. Так как 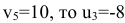. Система потенциалов установлена. Проверяем незанятые клетки на оптимальность.

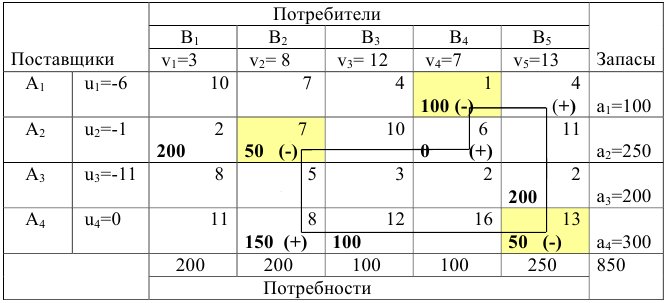
Клетки 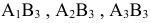не удовлетворяют условию оптимальности; находим для них величины разностей 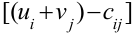и записываем в нижние левые углы этих клеток. Максимум разности находится в клетке 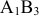, поэтому эта клетка подлежит загрузке; отмечаем эту клетку знаком (+) и строим цикл ( см. следующую таблицу)

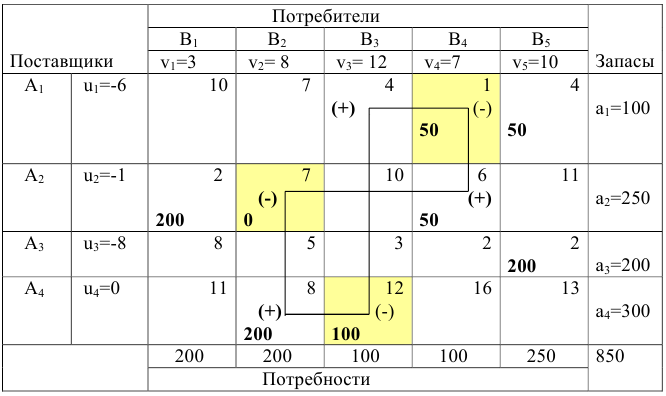
Находим величину

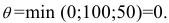
Нулевой груз перемещаем в клетку 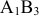, остальные клетки без изменения. Получили новый опорный план и изменяем систему потенциалов (см. следующую таблицу):

Пересчёт потенциалов: из клетки 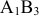получим 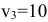; из клетки 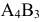следует 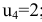; из клетки 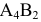вычислим .

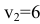Далее проверяем незанятые клетки на оптимальность. Все клетки удовлетворяют условию оптимальности, следовательно, план оптимальный.

Найдём общую стоимость составленного плана как сумму произведений объёмов перевозок на соответствующие стоимости в этих же клетках:

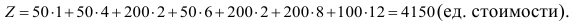
Ответ: план представлен таблицей, общая стоимость всех перевозок 4150(ед.стоимости).

Возможно эти страницы вам будут полезны:

Решение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюЛинейное программирование в Excel