Оглавление:

| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как заказать выполнение заданий по математической статистики
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько может стоить заказ математической статистики
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа
Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Чуть ниже я предоставила примеры оформления заказов по некоторым темам математической статистики, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.
Пример оформления заказа №1.
В результате проведения исследований получены следующие статистические данные (табл.1), где 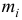 — частота попадания вариант в промежуток
— частота попадания вариант в промежуток 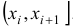 . Для выборки построить гистограмму относительных частот.
. Для выборки построить гистограмму относительных частот.
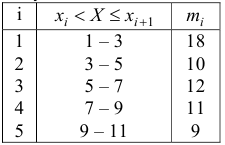
Решение:
Объём выборки 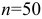 . Найдём относительные частоты:
. Найдём относительные частоты:
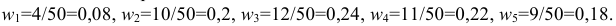
Найдём плотности относительных частот, учитывая, что длина интервала 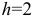 :
:
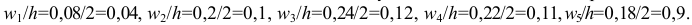
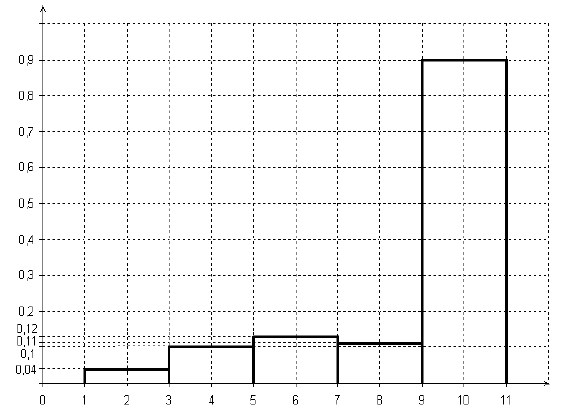
Построим на оси абсцисс данные частичные интервалы. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от неё на расстояниях, равных соответствующим плотностям относительной частоты.
Например, над интервалом (1,3) проведем отрезок, параллельный оси абсцисс и находящийся от неё на расстоянии, равном 0,04; аналогично строят остальные отрезки.
Искомая гистограмма относительных частот изображена на рисунке ниже.
Пример оформления заказа №2.
В ходе эксперимента получены данные наблюдений:

Для данной выборки выполнить следующее:
- Вычислить числовые характеристики выборки (мода, медиана, выборочное среднее, выборочная дисперсия, среднее квадратическое отклонение, начальные и центральные моменты);
- Найти несмещенные оценки генерального среднего и генеральной дисперсии.
- Определить тип распределения (симметричный — асимметричный, плосковершинный — островершинный).
- Построить эмпирическую функцию распределения;
Решение:
Найдем числовые характеристики данной выборки:
- Минимальное и максимальное значение выборки:
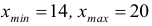 .
. - Размах выборки:
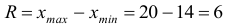 .
. - Мода:
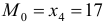 .
. - Так как вариационный ряд содержит четное число вариант
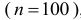 , то медиана
, то медиана 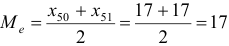 .
.
- Выборочное среднее:
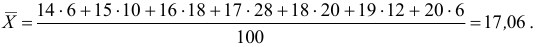
- Выборочная дисперсия:
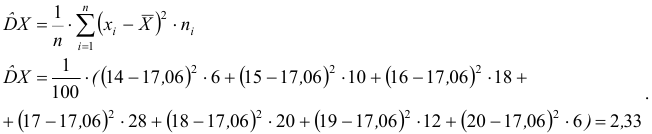
- Среднее квадратическое отклонение:
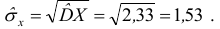
- Начальные моменты:
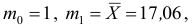

- Центральные моменты:
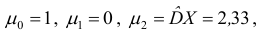
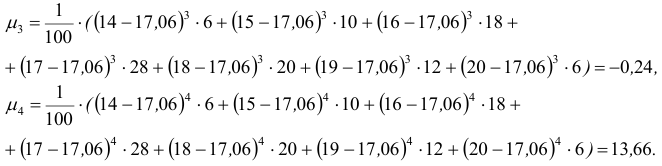
Несмещенной оценкой генерального среднего является выборочное среднее.
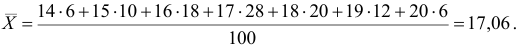
Для вычисления выборочной дисперсии воспользуемся формулой:
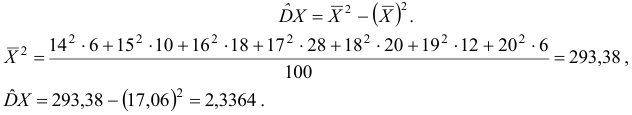
Находим несмещенную оценку дисперсии («исправленную» выборочную дисперсию):
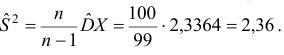
- Коэффициент асимметрии вычислим по формуле :
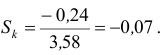
- Коэффициент эксцесса вычислим по формуле:
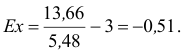
Поскольку 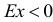 , то данное распределение является плосковершинным. Учитывая, что
, то данное распределение является плосковершинным. Учитывая, что 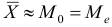 , можно считать распределение симметричным.
, можно считать распределение симметричным.
Запишем эмпирическую функцию данного распределения. Для этого найдем относительные частоты 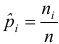 и результаты оформим в виде таблицы:
и результаты оформим в виде таблицы:

Тогда эмпирическая функция распределения 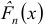 имеет вид:
имеет вид:
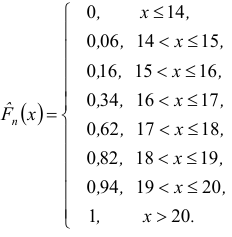
Пример оформления заказа №3.
Найти доверительный интервал для неизвестного математического ожидания 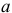 случайной величины
случайной величины 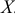 , распределенной нормально, если известны объем выборки
, распределенной нормально, если известны объем выборки 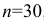 , выборочное среднее
, выборочное среднее 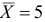 , надежность
, надежность 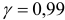 и среднее квадратическое отклонение
и среднее квадратическое отклонение 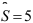 .
.
Решение:
Построим доверительный интервал для математического ожидания при неизвестном параметре 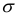 . Воспользуемся формулой (30):
. Воспользуемся формулой (30):
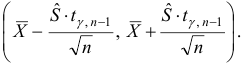
Для заданных 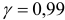 и
и 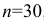 найдем значение
найдем значение 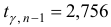 (см. Приложение 6). Тогда получим интервал, покрывающий
(см. Приложение 6). Тогда получим интервал, покрывающий 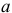 с надежностью 0,99:
с надежностью 0,99:
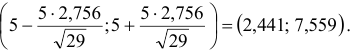
Пример оформления заказа №4.
Генеральная совокупность имеет нормальное распределение, для которого известно значение параметра 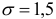 . Найти наименьший объем выборки, при котором доверительный интервал длиной
. Найти наименьший объем выборки, при котором доверительный интервал длиной 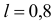 покрывает параметр
покрывает параметр 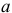 с надежностью
с надежностью 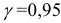 .
.
Решение:
Доверительный интервал для математического ожидания при известном параметре 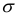 определяется формулой (25):
определяется формулой (25):
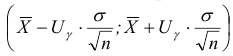
или
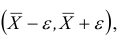
где
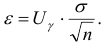
По условию 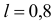 , значит,
, значит, 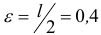 . Величину
. Величину 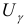 найдем из уравнения
найдем из уравнения 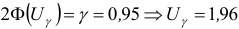 (см. Приложение 2). Тогда
(см. Приложение 2). Тогда
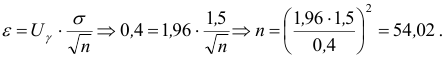
Следовательно, наименьшим объемом выборки будет
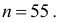
Пример оформления заказа №5.
Найти доверительный интервал для неизвестного среднего квадратического отклонения 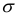 нормально распределенной случайной величины
нормально распределенной случайной величины 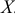 , если известны объем выборки
, если известны объем выборки 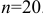 , надежность
, надежность 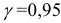 и выборочная дисперсия
и выборочная дисперсия 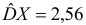 .
.
Решение:
Доверительный интервал для неизвестного среднего квадратического отклонения 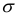 определяется формулой (37):
определяется формулой (37):
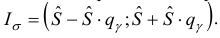
Вычислим
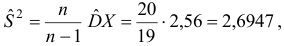
тогда
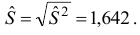
Найдем величину 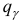 по известному
по известному 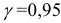 (см. Приложение 7):
(см. Приложение 7): 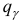 = 0,37. Следовательно, интервал (1,642 — 1,642 • 0,37;1,642 + 1,642 • 0,37) = (l,034;2,249) является доверительным для параметра
= 0,37. Следовательно, интервал (1,642 — 1,642 • 0,37;1,642 + 1,642 • 0,37) = (l,034;2,249) является доверительным для параметра 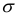 с надежностью
с надежностью 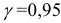 .
.
Возможно эти страницы вам будут полезны:
- Предмет теория вероятностей и математическая статистика Решение задач по теории вероятностей
- Помощь по теории вероятности
- Заказать работу по теории вероятности
- Контрольная работа по теории вероятности
- Курсовая работа по теории вероятности
- Решение задач по математической статистике
- Помощь по математической статистике
- Контрольная работа по математической статистике
- Курсовая работа по математической статистике
- Теория вероятностей краткий курс для школьников и студентов

