Оглавление:
| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как заказать выполнение заданий по линейному программированию
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько может стоить заказ линейного программирования
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа
Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Чуть ниже я предоставила примеры оформления заказов по некоторым темам предмета линейного программирования, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.
Основная задача линейного программирования
Формулировка основной задачи. Основная задача линейного программирования формулируется так:
Дана линейная форма (целевая функция)
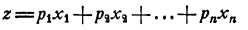
и задана система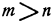 
линейных неравенств (ограничений)
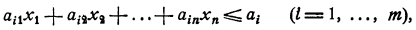
которую перепишем в виде
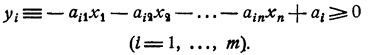
Найти максимум (минимум) формы (2.1) при выполнении условий (2.2).
Другими словами, среди решений системы (2.2) (образующих многогранник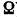 
) надо отыскать такое, для которого форма (2.1) принимает наибольшее (наименьшее) значение.
Как будет показано в следующей главе, эта задача служит математической моделью многих важных практических задач.
- Геометрическая интерпретация. Основную задачу линейного программирования можно легко интерпретировать геометрически. Каждое неравенство
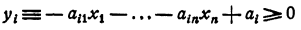
системы (2.2) определяет в евклидовом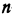 
-мерном пространстве полупространство, состоящее из точек 
расположенных «по одну сторону» от плоскости
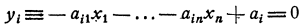
и на самой этой плоскости. Точки же, принадлежащие всем полупространствам (2.2) (т. е. множество всех решений системы (2.2)) как пересечение выпуклых множеств, образуют некоторый выпуклый многогранник *).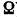
Значение функции
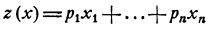
в точке 
можно рассматривать как уклонение точки от плоскости
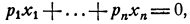
понимая (как в п. 2 § 1 гл. I) под уклонением данной точки от этой плоскости число, которое получим, подставив в левую часть уравнения (*) вместо 
координаты 
этой точки. Так, например, уклонение точки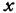 
(1, —2, 5) от плоскости
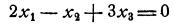
равно числу
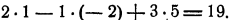
Уклонение точки 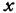от плоскости (*) пропорционально расстоянию от точки 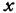до этой плоскости.
Таким образом, геометрический смысл задачи линейного программирования заключается в отыскании в многограннике 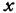точки, которая наиболее (наименее) уклонена от плоскости (*).
В случае двумерного пространства имеем картину, изображенную на рис. 1—4.
Здесь многогранником 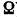является многоугольник, плоскостями
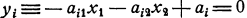
прямые, полупространствами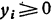 
— полуплоскости (на рисунках они отмечены штриховкой).
Ясно, что решением задачи линейного программирования будет какая-то вершина многогранника 2. На рис. 1 решение задачи максимизации формы (2.1) дает вершина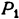 
, а задачи минимизации этой формы —вершина 
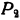, причем эти решения единственны.
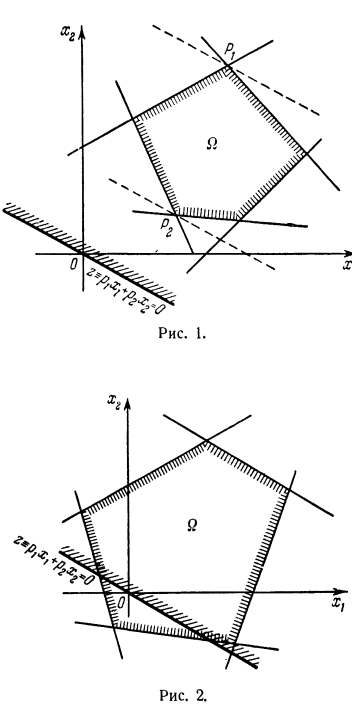
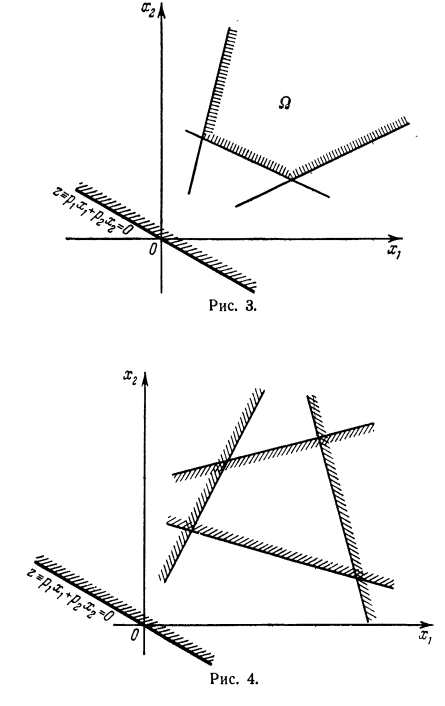
На рисунках 2 — 4 приведены: случай существования бесчисленного множества решений (рис. 2), случай неограниченности функции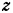 
на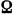 
(рис. 3) и, наконец, случай отсутствия решения (рис. 4).
Другую геометрическую интерпретацию задачи линейного программирования получим, если будем рассматривать эту
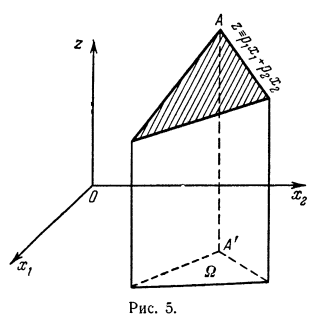
задачу в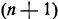 
-мерном пространстве переменных 
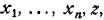в котором линейная форма
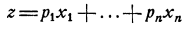
является уравнением плоскости (проходящей через начало координат). Система же неравенств
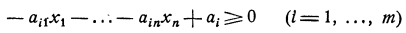
определяет в этом пространстве некоторую выпуклую призму гранями (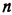
-мерными) которой служат плоскости
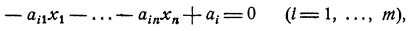
параллельные оси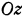 
. В «горизонтальной» плоскости 
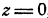, т. е. в л-мерном пространстве переменных 
эти плоскости ограничивают многогранник 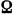, на который проектируется часть плоскости (2.1)—«срез», вырезаемый призмой (2.2), так что 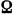можно рассматривать как область определения линейной функции (2.1). Надо найти ту из вершин 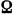, в которую проектируется вершина «среза» с наибольшей (наименьшей) координатой (в трехмерном пространстве — аппликатой) .
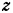На рис. 5 изображение дано для случая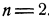 
. «Срез» заштрихован. Наибольшее на 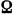значение линейная функция (2.1) достигает в вершине 
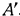, в которую проектируется вершина 
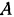«среза» с наибольшей аппликатой.
О методе решения задачи линейного программирования. Нетрудно понять, что обычные методы классического математического анализа для отыскания наибольшего (наименьшего) значения функции неприменимы к рассматриваемой задаче.
Эти методы, сводя задачу к отысканию множества точек, «подозрительных на экстремум», и к сравнению значений функции в этих точках, становятся малопригодными, если число таких точек велико.
Линейная же форма (2.1), определенная на многограннике 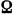, заданном неравенствами (2.2), достигает своего наибольшего (наименьшего) значения в некоторой вершине этого многогранника, так что множеством точек, «подозрительных на экстремум», является множество всех вершин многогранника , число которых обычно бывает огромным.
Основным методом решения общей задачи линейного программирования, позволяющим преодолеть эти затруднения, является так называемый симплекс-метод Данцига [30а, 306], подробное описание которого дано в §§ 2, 3.
Симплекс-метод состоит из алгорифма отыскания какого-нибудь опорного среди решений системы линейных неравенств (2.2), т. е. решения-вершины многогранника (или из установления факта несовместности системы), и из алгорифма последовательного перехода от полученного уже опорного решения системы (2.2) к новому опорному решению, для которого форма (2.1) имеет большее (меньшее) значение (до получения максимизирующего (минимизирующего), т. е. оптимального решения).
Основу вычислительной схемы симплекс-метода составляют модифицированные жордановы исключения.
| Предмет математическое программирование |
Пример оформления заказа №1.
Найти какое-нибудь опорное
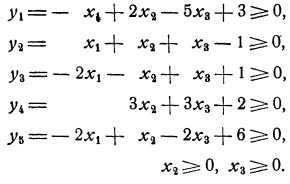
Составляем таблицу
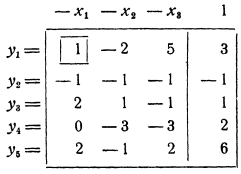
и исключаем лишь свободную переменную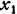 
(см. замечание в конце п. 2). Для этого делаем шаг модифицированного жорданова исключения с разрешающим элементом 1, взятым в рамку. Получим таблицу
из которой выписываем выражение для :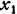
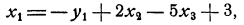
и переходим к отысканию опорного решения. Третья строка содержит отрицательный свободный член. В этой же строке есть два отрицательных коэффициента — 2 и — 11. Выбираем в качестве разрешающего, например, первый столбец, содержащий коэффициент — 2, и сравниваем все неотрицательные отношения свободных* членов к соответствующим коэффициентам первого столбца:
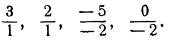
Меньшее из них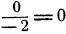 
, однако в случае вырождения мы берем знаменатель разрешающим элементом, лишь если он положителен. Поэтому берем следующее по величине отношение 
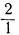у и его знаменатель 1 будет разрешающим элементом.
После шага модифицированного жорданова исключения получим таблицу
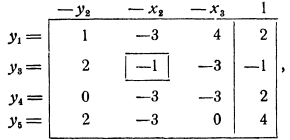
в которой остался отрицательный свободный член —1. Превратим его в положительный, сделав шаг модифицированного жорданова исключения с разрешающим элементом — 1, взятым в рамку, так как есть всего одно положительное отношение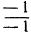 
свободных членов к коэффициентам второго столбца, взятого разрешающим.
Из полученной таблицы
в которой нет отрицательных свободных членов, находим опорное решение нашей системы. Для этого полагаем
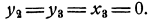
Тогда
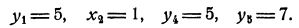
Подставив значения для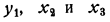 
в выражение для 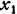находим
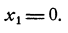
Мы получили, таким образом, следующее опорное решение:
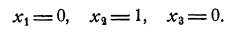
Пример оформления заказа №2.
Найти опорное решение системы
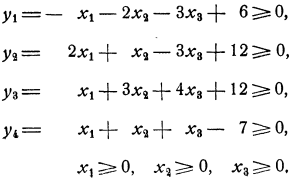
Составляем таблицу
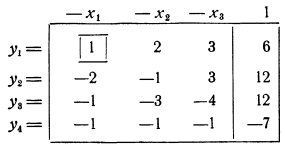
и приступаем к отысканию опорного решения системы, не производя исключения координат.
Четвертая строка содержит отрицательный свободный член —7. Просматриваем, например, первый столбец коэффициентов, содержащий отрицательный коэффициент —1 этой строки, составляем неотрицательные отношения свободных членов к коэффициентам этого столбца и находим наименьшее из них:
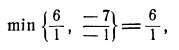
так что разрешающим элементом будет 1 из первой строки.
В результате шага модифицированного жорданова исключения с этим разрешающим элементом получаем таблицу
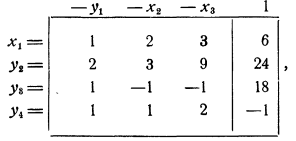
в которой еще остается отрицательный свободный член —1, но строка, в которой он находится, не содержит отрицательных коэффициентов, следовательно, система несовместна.
Возможно эти страницы вам будут полезны:
