Во многих процессах и явлениях, встречающихся в природе, в практической деятельности человека, числовые значения одной величины определяются набором из двух, трех и большего количества независимых переменных. При изучении подобных зависимостей используют понятие функции нескольких переменных.
Обратимся к задачам, приводящим собственно к этому понятию.
Задача 1: Если через 
и 
обозначить длины сторон прямоугольника, то его площадь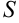 
выражается формулой 
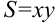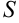. При изменении и меняется и площадь . В этом случае говорят, что площадь 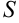есть функция двух переменных и , заданная формулой .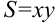
Задача 2: Дальность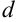 
полета тела, брошенного с начальной скоростью 
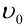под углом 
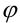к горизонту, также является функцией двух переменных 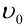и 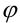и задастся формулой 
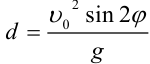, где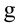 
— ускорение силы тяжести.
Задача 3: Объем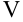 
прямоугольного параллелепипеда с ребрами, длины которых равны , и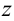 
, является функцией трех переменных , и 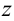и задастся формулой 
.
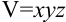Задача 4: При изучении свойств нагретого тела его температура рассматривается обычно переменной величиной, зависящей от точки, в которой измеряется температура, и от момента времени, в который проводится измерение.
Если точка имеет координаты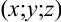 
, тогда зависимость температуры 
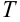от координат точки и момента времени 
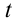обозначается следующим образом: 
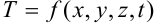, то сеть температура 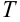является функцией четырех переменных. Переменные 
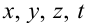— независимые переменные, они могут принимать любые допустимые значения. Переменная 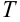является зависимой переменной, значения которой определяются значениями независимых переменных .
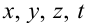В дальнейшем остановимся на подробном изучении функции двух переменных, так как все важнейшие факты теории функции нескольких переменных наблюдаются уже на функциях двух переменных. Распространение определений и полученных результатов на функции трех и более переменных представляет собой, как правило, лишь технические трудности.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Несобственные интегралы I рода. |
| Несобственные интегралы II рода. |
| Понятие функции двух действительных переменных. |
| Способы задания функции двух действительных переменных. |
