Задачи, решение которых приводится к интегрированию дифференциальных уравнений, содержащих производные или дифференциалы неизвестных функций, весьма разнообразны. В таких задачах ищется функция или зависимость между переменными факторами какого — либо физического, химического или технического процесса, уравнение линии или поверхности.
При решении этих задач вначале составляется дифференциальное уравнение задачи, которое затем решается тем или иным способом в зависимости от его типа.
Пример:
Моторная лодка движется со скоростью 18 км/ч. Через 5 мин после выключения мотора ее скорость уменьшилась до 6 км/ч. Найти расстояние, пройденное лодкой по инерции за 15 мин, если сопротивление воды пропорционально скорости движения лодки.
Решение:
Пусть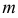 
— масса лодки, 
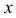— путь, пройденный ею за время 
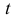, отсчитываемое от момента выключения двигателя, 
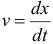— скорость лодки в момент времени 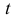. Тогда, согласно второму закону Ньютона, дифференциальное уравнение движения лодки будет
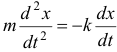или 
.
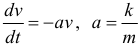Разделяя переменные и интегрируя, получим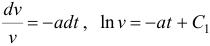 
.
Исходя из начального условия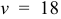 
при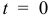 
, определяем значение постоянной 
.
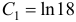Следовательно,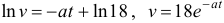 
.
Найдем параметр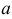 
из условия, что через 5 мин = 1/12 ч скорость лодки стала 6 км/ч: 
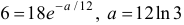. Следовательно, 
.
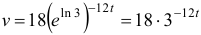Т. к. 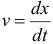, то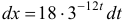 
. Интегрируя, получим 
.
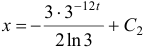Исходя из начального условия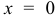 
при 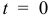, определяем значение постоянной 
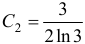. Следовательно, 
.
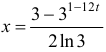За 15 мин = 1/4 ч лодка пройдет расстояние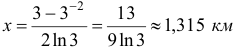 
.
Ответ: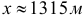 
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Сведение системы к одному дифференциальному уравнению высшего порядка |
| Решение систем дифференциальных уравнений с помощью характеристического уравнения |
| Числовые поля |
| Комплексные числа |
