Задача о проведении касательной к кривой

Оглавление:

Задача о проведении касательной к кривой

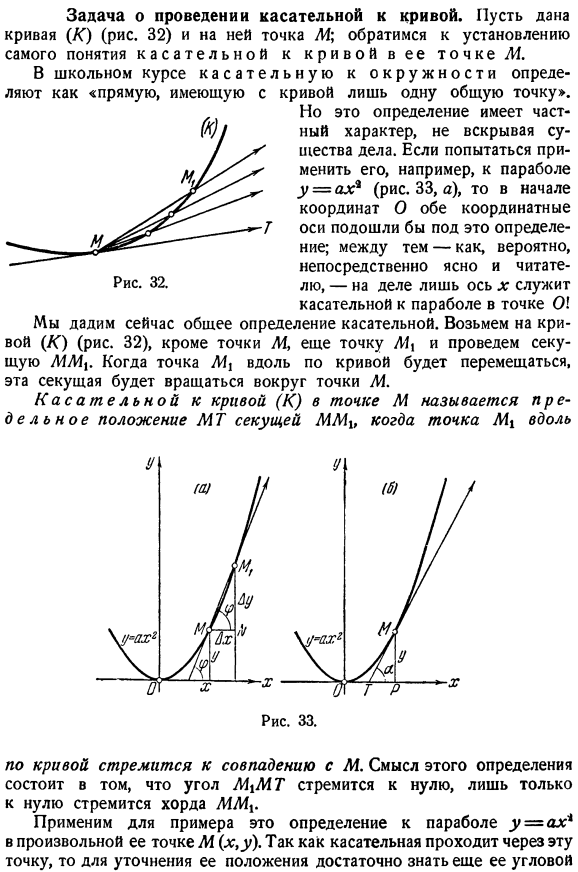
Задача о проведении касательной к кривой. Дайте кривую (K) (рис.32) и поместите на нее точку M. Перейдем к установлению понятия касательной кривой в точке М. В школьном курсе тангенс окружности определяется как » линия с только 1 общим знаменателем, имеющим кривую». Однако это определение носит частный характер и не раскрывает сути проблемы. Например, если вы попытаетесь применить его к параболе y-ax1 (рис. 33, а), то в начале координат O обе оси соответствуют этому definition.

Между тем-как, возможно, непосредственно очевидно читателю-на самом деле только ось x касательна к параболе в точке О. Людмила Фирмаль

Вот общее определение tangents. In кроме точки M, возьмите кривую (K) (рис.32) и нарисуйте секущую LS|.Когда точка м движется по кривой, эта секущая вращается вокруг точки М. Касательная кривой в точке M (K) равна точке M Кривая стремится соответствовать M. смысл этого определения заключается в том, что угол M \ MT стремится к нулю, и только код MM \стремится к нулю. Например, примените это определение к любой точке M (x, y) параболы y = ax.Поскольку касательная проходит через эту точку, достаточно знать угловой коэффициент, чтобы уточнить ее местоположение.

Поставлена задача найти угловой коэффициент касательной в точке М. После придания абсциссе x приращения Ддг, переходим от точки M кривой к абсциссе X \ KX и к точке MX с ординатой. КСУ = а (xDx) в (Рис. 33, а).Угловой коэффициент 1 ^ 9 секущего мм \определяется из прямоугольного треугольника MYM. In в этом случае катестат WE равен приращению абсциссы kx, а катестат YM \явно соответствует приращению ординаты АУ = А (2х * але-| Ал; 2）、 Как это = = + Al; * 0.

Нетрудно понять, что для получения углового коэффициента касательной необходимо достичь предела. Людмила Фирмаль

Это потому, что он эквивалентен коду MM \ > 0.At в то же время (rcha и (функция смежности* 8 <p） Поэтому мы достигнем результата. а = Иш(2ax-| НДЗ;)= 2ax*). Ддг-о Для кривых с равенством У = F(х） Наклон касательной также устанавливается. Инкрементальный ад: абсцисса соответствует приращению Ординаты Au, а отношение равно А то. Да. Представляет угловой коэффициент секущей (&<p. угловой коэффициент касательной получается отсюда путем перехода к пределу с Dd;» −0： * ЭА = НС <8 <р = н «н» н Ддг Л Ам-Л Ол.

Теорема о равномерной непрерывности.	Определение производной.
Задача о вычислении скорости движущейся точки.	Примеры вычисления производных.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.