К понятию определённого интеграла приводят множество прикладных задач:
- вычисление площади криволинейной трапеции;
- вычисление работы, которую совершает переменная сила при перемещении материальной точки из одного положения в другое;
- вычисление объёма произведенной продукции за определенный промежуток времени при переменной производительности труда.
Пусть на отрезке 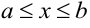 определена функция
определена функция 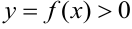 (рисунок 7.1). Вычислим площадь фигуры
(рисунок 7.1). Вычислим площадь фигуры 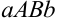 , коротая ограничена графиком функции
, коротая ограничена графиком функции 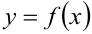 , осью
, осью 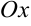 и прямыми
и прямыми 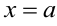 и
и 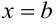 (фигуру
(фигуру 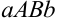 называют криволинейной трапецией). Для этого отрезок
называют криволинейной трапецией). Для этого отрезок 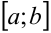 точками
точками 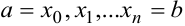 разбиваем на
разбиваем на 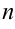 частей, внутри каждого частичного интервала
частей, внутри каждого частичного интервала 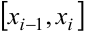 выбираем произвольную точку
выбираем произвольную точку 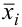 .
.
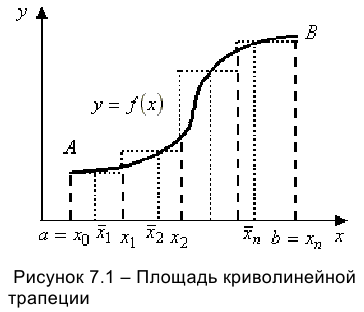
Если принять значение функции в каждом частичном отрезке постоянным и равным 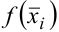 , то криволинейная трапеция будет заменена ступенчатой фигурой, площадь которой определяется по формуле
, то криволинейная трапеция будет заменена ступенчатой фигурой, площадь которой определяется по формуле 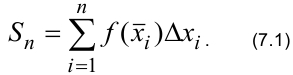
Сумма (7.1) называется интегральной суммой функции 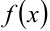 на отрезке
на отрезке 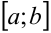 , где
, где 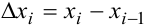 — длина частичного интервала. Площадь
— длина частичного интервала. Площадь 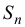 приблизительно равна площади криволинейной трапеции
приблизительно равна площади криволинейной трапеции 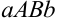 .
.
Определение. Если существует предел интегральных сумм 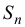 при условии, что
при условии, что 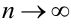 и длина каждого частичного отрезка стремится к нулю, не зависящий от способа разбиения отрезка
и длина каждого частичного отрезка стремится к нулю, не зависящий от способа разбиения отрезка 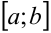 на частичные отрезки и от выбора точек
на частичные отрезки и от выбора точек 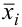 , то он называется определённым интегралом от функции
, то он называется определённым интегралом от функции 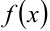 в пределах от
в пределах от 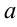 до
до 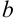 и обозначается символом
и обозначается символом
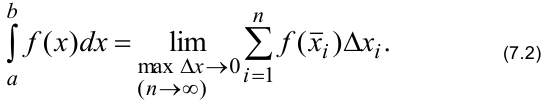
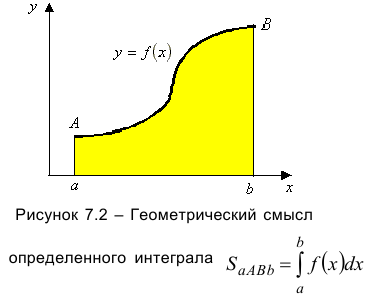
При этом определённый интеграл равен площади криволинейной трапеции 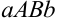 , ограниченной графиком функции
, ограниченной графиком функции 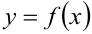 , осью
, осью 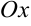 и прямыми
и прямыми 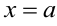 и
и 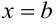 . В этом состоит геометрический смысл определенного интеграла (см. рисунок 7.2).
. В этом состоит геометрический смысл определенного интеграла (см. рисунок 7.2).
Название элементов определенного интеграла 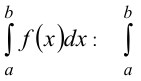 — знак определенного интеграла, где
— знак определенного интеграла, где 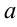 — нижний предел,
— нижний предел, 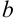 — верхний предел интегрирования;
— верхний предел интегрирования; 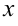 — переменная интегрирования;
— переменная интегрирования; 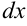 — дифференциал переменной интегрирования;
— дифференциал переменной интегрирования; 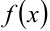 — подынтегральная функция;
— подынтегральная функция; 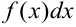 — подынтегральное выражение.
— подынтегральное выражение.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Интегрирование тригонометрических функций |
| Интегрирование иррациональных функций с помощью тригонометрических подстановок |
| Все свойства определённого интеграла |
| Формула Ньютона — Лейбница |
