Взаимная обратность задач проведения касательной и квадратуры

Оглавление:

Взаимная обратность задач проведения касательной и квадратуры

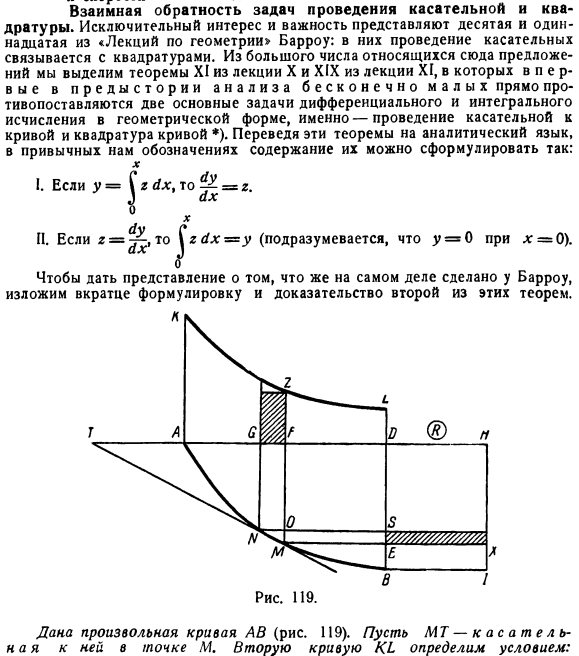
Взаимная обратность задач проведения касательной и квадратуры. Исключительный интерес и значение представляют 10-я и 11-Я части «лекции по геометрии > Кургана», в которых проведение касательных связано с квадратурой. Здесь мы выбираем теорему XI из лекции X, а теорему XIX из лекции XI из ряда связанных предложений. Впервые в истории проведен анализ 2-х основных задач исчисления в геометрической форме, с точностью до наоборот. То есть, проведя касательную линию кривой и переведя эти теоремы 2) на аналитический язык, в знакомой нам нотации, мы можем сформулировать их содержание следующим образом: 1. если y = ^ r dx, то^■= C r. Ага. Если * = 0, ТО 0). Второй. 2 = тогда г = г(г Дана любая кривая AB(рис. 119). Пусть MT-касательная в точке M. условие определяет 2-ю кривую K1. Э2:э-эм \ Тэ. Где K-заданный отрезок (=OH). в этом случае площадь AQ умножается на yB X /?Она будет равна. Для доказательства возьмем кривую AB » бесконечно малый отрезок WE и проведем линию, указанную на чертеже.

Гораздо больше делается в областях, связанных с интегральными расчетами. Людмила Фирмаль

Затем(как вы уже знаете） МО: ч0 = ГМ: тг = Е2:к、 Откуда Ч0 х Е2-МО х /?Или OE X E2-E $ X EX. «Но утверждение очень ясно, потому что каждый прямоугольник OE x E2 сколь угодно мал, как область AOBX и возможно, и каждый соответствующий прямоугольник E $ X EX образует прямоугольник OSB.」 AE-x, EM = y, E2 = r и p = 1, в зависимости от условий, определяющих 2-ю кривую、 Джем ты. Тэ-ых Т» • И вывод теоремы икс ^ РГК-ый 1-й. О Но даже простое сравнение этих 2 теорем из Кургана было бы бесполезно искать (в книге его отделяют 2 десятка других теорем). кроме того, они редко используются. Здесь сказалось лишь то, что Барроу говорит на геометрическом языке, не зная общей концепции, которая могла бы раскрыть суть проблемы и открыть путь к широкому кругу применений. Предыдущий обзор.

Подведем итог тому, что было достигнуто в направлении «анализа бесконечно малого» в 17 веке, до появления в математической области Ньютона и Лейбница. Здесь было получено не только большое количество конкретных результатов относительно квадратурного, квадратурного, дугового прямолинейного, поверхностного компарационного и центроидного определения, но и соотношения между всеми подобными задачами, которые традиционно сводились к простейшим из них realized. In в работах Кавальери, Паскаля и других, понятие определенного интеграла начало формироваться clarified. In фактически, многие из простейших интегралов были вычислены, чаще всего в геометрической форме, но иногда чисто арифметической(ферма, Паскаль, Уоллис).Я нашел различные отношения, которые преобразуют некоторые интегралы в другие (ферма, Паскаль, Барроу).

В области, которая теперь называется дифференциальным исчислением, ферма предоставил единый метод микроскопических свойств для нахождения наибольших или наименьших касательных и решения задачи построения касательных. Его исследования были продолжены несколькими другими авторами. Однако определить основные понятия, лежащие в основе концепции, не удалось. problem. In в частности, попытки Роберта Барбара и Торричелли, к которым продолжил Барроу, решали проблему вычерчивания касательных в кривой на основе кинематических соображений (это впоследствии нашло отражение в концепции Ньютона). Наконец, как мы видели ранее, Барроу смог частично перекинуть мостик от одной групповой задачи к другой групповой задаче.

Таким образом, была подготовлена основа для нового расчета, но собственного расчета по-прежнему не было. Но с другой стороны, Лейбниц тогда добавил: «после таких успехов в науке не хватало только одного.»Задача лабиринта, то есть алгебраическая модель аналитических вычислений нити Ариадны«.Здесь, прежде всего, необходимо было установить в общих чертах основные понятия нового расчета и его соотношения. Затем, введя соответствующую символику, необходимо было создать периодические процессы или алгоритмы для вычислений. Это делалось независимо друг от друга Ньютоном и Лейбницем), причем делалось по-разному.

Это понятие бесконечно мало, «актуально», противоречиво и таинственно по своей природе, наряду с понятием числа и пространства. Людмила Фирмаль

Рецензии на их работы, связанные с анализом бесконечно малого, предшествуют следующим утверждениям о самом понятии «бесконечно малое», причем-и уже давно-они подразумевают бесконечно или бесконечно малое, часто, не говоря об этом явно, так сказать статическое, то есть значение меньше конечного, которое не равно нулю (абсолютно) неизменному. Это хорошо известно теперь понятием бесконечно малого «потенциально» как переменной, но оно противопоставляется понятию меньшего, чем конечные значения, только в ходе этого изменения. Переход от мизерного понимания к другим пониманиям сопряжен с огромными трудностями, поскольку они требуют четкого представления о конечном процессе. Борьба между этими двумя понятиями Ци.

Нахождение наибольших и наименьших, проведение касательных.	Исчисление флюксий.
Проведение касательных с помощью кинематических соображений.	Исчисление, обратное исчислению флюксий; квадратуры.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.