Выражение площади интегралом

Оглавление:

Выражение площади интегралом

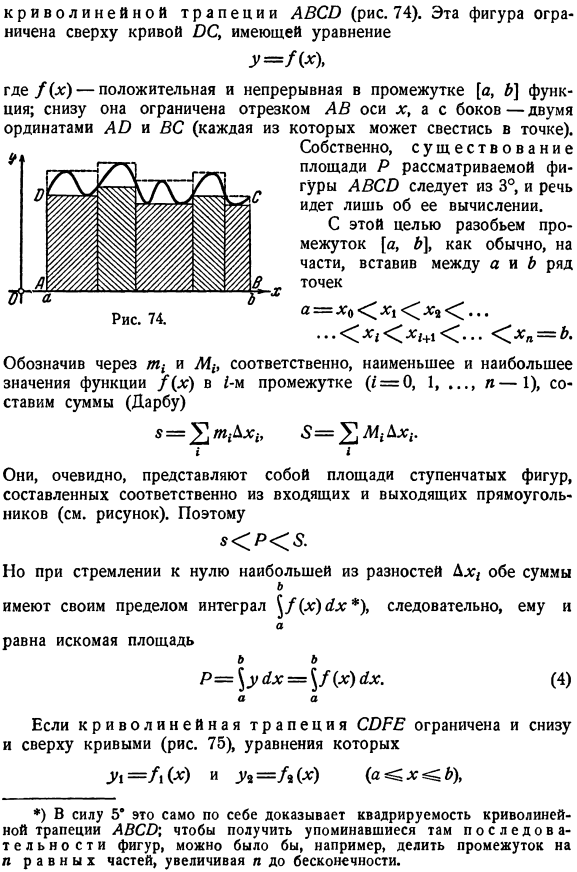
Выражение площади интегралом. Далее переходим к расчету площади плоского участка с помощью интеграла. В первую очередь, со строгим описанием, мы рассмотрим впервые проблему определения территории, с которой мы уже столкнулись. Изогнутая трапециевидная АБКО(рис. 74).Эта фигура ограничена сверху кривой операционной системы с помощью следующего уравнения У = РХ）、 Где f (x) положительная непрерывная функция интервала[a, b].Снизу она ограничена отрезком оси Х AB, а с боков двумя ординатами AO и BC (каждая из которых собрана в 1 точке). На самом деле, рассматриваемая фигура наличие области P ABCy продолжается от 3°и говорит только о ее расчете. Для этого разделите интервал[a, b) на части, как обычно, и вставьте ряд точек между a и b * * ■ СИ ^-^ / + 1 хп = б * m1, и соответственно, первый интервал(/ = 0, 1.

Очевидно, что они представляют собой область ступенчатых чисел, каждое из которых состоит из входящего квадрата и исходящего прямоугольника. Людмила Фирмаль

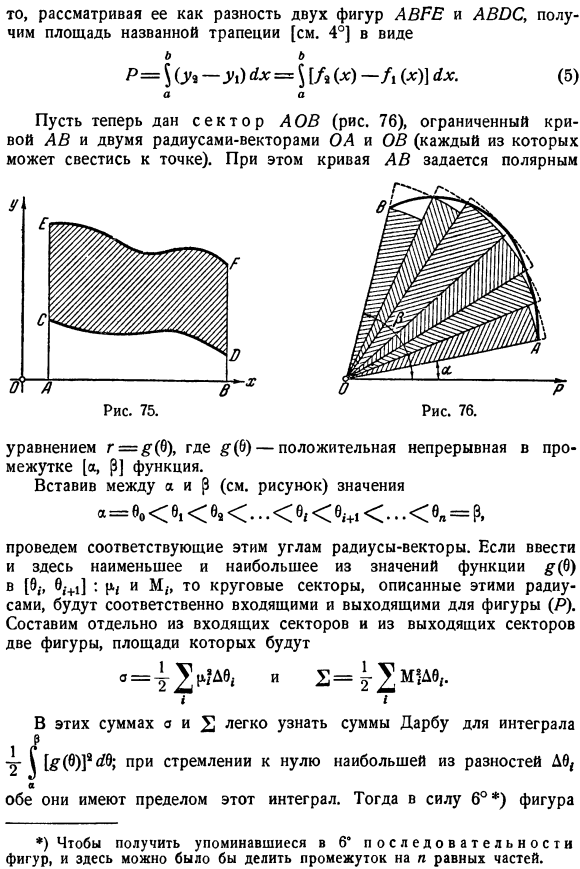
Я функции f (x), n-1, обозначают минимальное и максимальное значения суммы (Дарбу). 8 = ’21 м, bx1, 3 = ’^ M1′. (см. Рисунок)… Однако, если вы стремитесь к нулю максимума различий, то сумма Длг/обоих б Существует ограничение на интегралы$ / (x) x), поэтому、 Но… Равна нужной площади б Р = ^ ух = $ /() (4） Но、 Если трапеция окружена как нижней, так и верхней кривой (рис. 75), то ее уравнение Y1 = A (X) и A = / * ( * ) (W * » 2 6）、 * ) На 5 * это доказывает ортогональность кривой трапеции ABC \, чтобы получить последовательность чисел, перечисленных там. Например, разделите зазор на n равных частей и увеличьте n бесконечно. Тогда примем его за разность между 2 фигурами Абре и ЛЯОС и получим площадь названной трапеции в виде [Ссылка 4° б П = (г -г )ух = \ [а()-а ()] ЛК. (5） Но.

Здесь мы показываем сектор AOB (рис. 76), окруженный кривыми AB и 2 векторами радиусов OA и OB(каждый из которых может быть сведен к точке). В этом случае кривая AB устанавливается на полюс По уравнению r=) (0), Где б (b) положительная непрерывная функция интервала[a, p]. вставка значений между cals(см. Рисунок) а = ор Б1 е… е, 0 ^ 1… БН = п、 Рисует радиус-вектор, соответствующий этим углам. Здесь.[0（-、0; +1] если ввести минимальное и максимальное значения функций^(0): (A и M, -, то круговые сектора, описываемые этими радиусами, соответственно, будут входными и выходными фигурами( P).Давайте создадим 2 отдельные диаграммы входных и выходных секторов. о = м2 /?’and2 н0 = ^ 2ЩЛ9’Я.

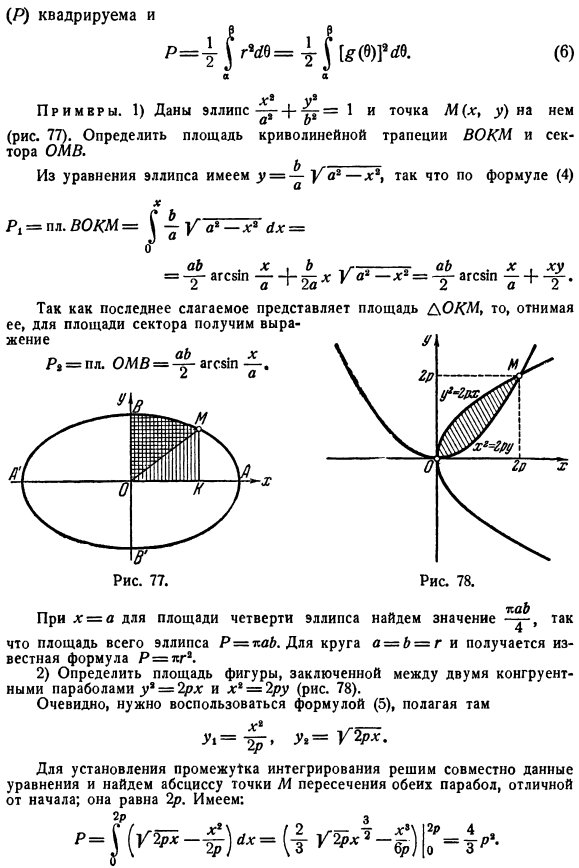
Тогда спасибо цифре 6° * ) Чтобы получить последовательность чисел, перечисленных в 6*, здесь мы можем разделить пробел на n равных частей. * В * г * Пример 1) учитывая эллипс^ = 1 и точку M (x%y) (Рисунок 77). Определите площадь кривой трапеции в СМ и сектор HF. Из эллиптического уравнения y = Ya% x \получается и по формуле (4) Икс РГ = ЛП. ВОКМ = ^ в * Х3-4х = ab пользовательский интерфейс. Х б 5 г Б. Х Ху = tagC5 | Нм + 2Bx y * х = xagC8Wm + Т1• Поскольку последний член представляет собой площадь DO # M, мы удаляем его и получаем следующую формулу для площади сектора: (P)является 2-м、 П Я{ГЖД = 11 [(«)? ＆ (6） X = o в районе квартала Площадь всего эллипса равна P = paL.

О круге a ^ xb-r мы получаем известную формулу P = m. 2) определить площадь фигуры, ограниченную двумя совпадающими параболами y * = 2px и X% 2pu(рис. 78). У1 = Х1 2Р> г,= г $ Военторга. Очевидно, что он должен быть установлен с помощью формулы (5 Чтобы установить интервал интегрирования, решите эти уравнения вместе и найдите координаты абсцисс пересечения M обеих парабол, отличные от первой. Он равен 2p. мы имеем： 3) уравнение(4) представляет собой кривую трапеции, граничная кривая которой является параметром или уравнением* =((),.y = 4(0 (0 Изменение переменной в Интеграле (4) дает следующую формулу (предполагая, что c =(0 и X = A, если X =b равно I = Γ): г т т ■= \ ух \ у = С {、 Да.） 4 *(0? (Л.

В этих суммах легко найти сумму Дарбоу интеграла, так как наибольшая разница стремится к нулю. Оба имеют этот интегральный предел. Людмила Фирмаль

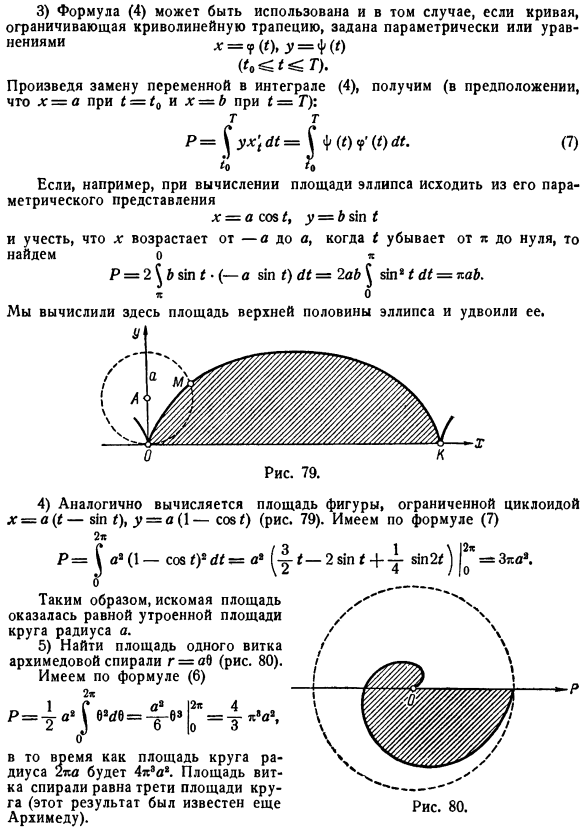
Например, если вы хотите вычислить площадь эллипса, перейдите к его параметрическому представлению х = со $ я, Г = Б 5!н и И учитывая, что x увеличивается от—o до a, а% уменьшается от n до нуля, o *найдено. Р = 2 ^ б $ 1Н б *(-в 5Б я) ч = 2ab ^ НН» 1y1 = ка. * О 4) аналогичным образом вычисляется площадь фигуры, окруженной циклоидой η=((*o, y = a (\so O (рисунок 79))). Два * P ^ a *(1-соя 0 * * и-a * Здесь мы вычислили площадь верхней половины овала и умножили ее в 2 раза. Таким образом, получается, что искомая площадь равна в 3 раза площади окружности радиуса А. 5) найти область arcimedes спираль г-АВ (рис. 80) 1 очередь. По Формуле (6) Завывание в области окружности радиуса 2pa будет 4k * o*.Площадь спирали равна 3 из 1 площади окружности(этот результат уже известен Архимеду.

Аддитивность площади.	Определение понятия объема, его свойства.
Площадь как предел.	Выражение объема интегралом.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.