Выражение объема интегралом

Оглавление:

Выражение объема интегралом

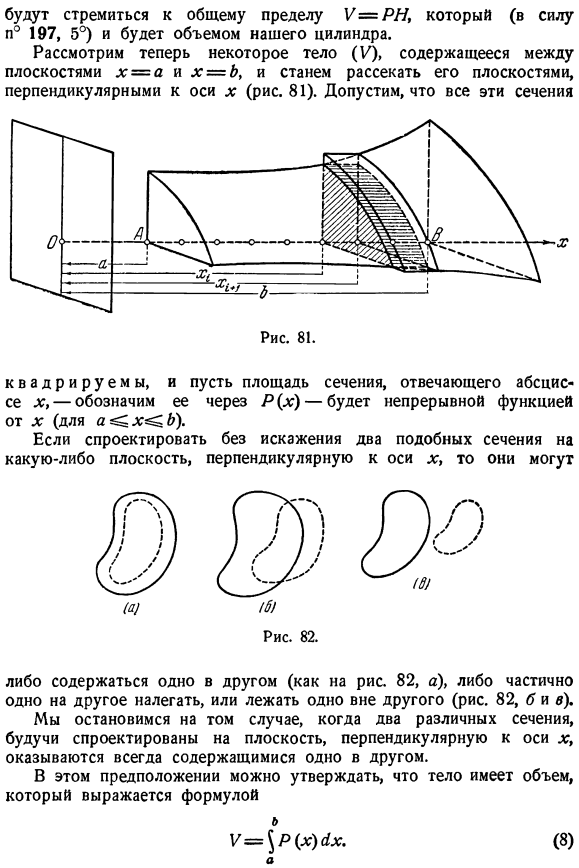
Выражение объема интегралом. Начнем с почти однозначного замечания: прямая овальная колонна высотой I(где низ-вторичный вид в плане (P)) имеет объем, равный площади дна и произведению высоты: Y = PH. Он принимает полигоны (Bn), содержащие (An) и (P), содержащиеся в (P), соответственно, и их площадь An и VL имеют тенденцию быть P [N°196, 5°].Если построить высоту H прямой призмы (Xn) и (Yn) на этих полигонах, то ее объем Xa = ApN и Vn = VPM Общий предел V = стремится к PH, который будет равен объему цилиндра (n°197 на 5°). Теперь рассмотрим объекты (V), находящиеся между плоскостями x = a и x = b, и разрежем их в плоскости, перпендикулярной оси x(рис.81).Эти разделы все Пусть это непрерывная функция-x (a x b), обозначаемая поперечным сечением-H(x;), соответствующим абсциссе X.

В соответствии с этим предположением тело имеет объем, который является формулой (8). Людмила Фирмаль

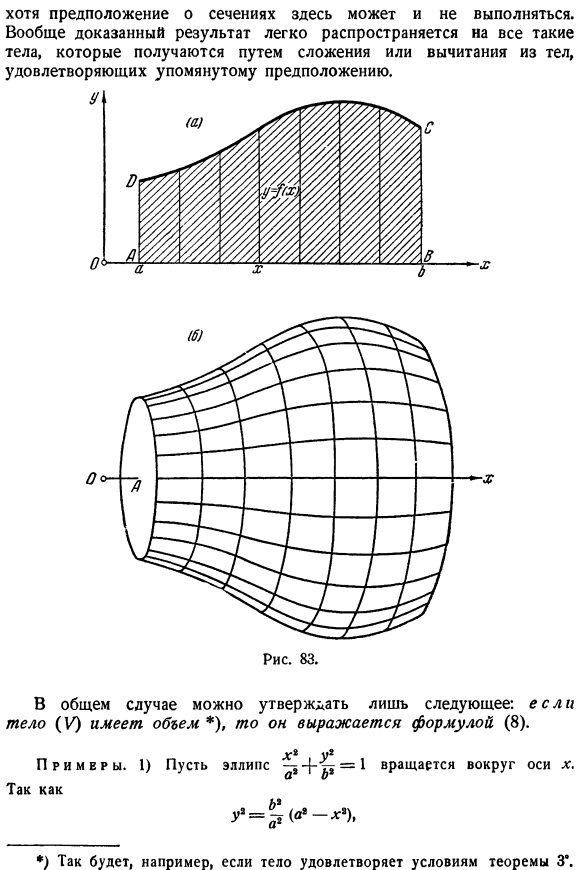
Если 2 подобных участка проецируются на плоскость, перпендикулярную оси x, без каких-либо искажений, то они являются 82, как и в случае а, одно входит в другое, или частично перекрывает другое, или одно находится вне другого(рис.82, в, iv). рассмотрим случай, когда 2 различных участка, которые проецируются на плоскость, перпендикулярную оси x, всегда включены друг в друга. Г = \ п (х) c1x. Но… Чтобы доказать это, сегменты на оси x [a, B \point d—X0* ^ 1■■ / +！ ==＆ Разделенный на части, через точку деления разлагается нарисованная плоскость x = x1r, и все тело становится слоем. Рассмотрим i-й слой, находящийся между равниной x = x {и x = xm (1 = 0, 1, n-1). в интервале[l :; xx] максимальное значение функции P(x) равно M1, минимальное/ ha и -;.

Если поперечное сечение, соответствующее различным значениям x в этом интервале, расположено на одной плоскости, например, x = x (тогда, согласно сделанным предположениям, они входят в Наибольшую в области A^, а в наименьшую в области mk. Постройте прямой цилиндр высотой Ax {= x ^ 1-x в этих максимальных и минимальных сечениях, причем больший из них будет содержать рассматриваемые слои нашего тела, а меньший будет находиться в этом слое. Каждый из них будет MX XX и M1 ^x 1. Корпус (T) состоит из входящего цилиндра, а корпус© из выходящего цилиндра. Их объем равен друг другу 2 max1 и 2 налога Мне.（ И затем В Когда Ищу. О1СО Мощность n4 ′ 197, 6°.Такие как До нуля, A =Max, имеет общий предел(8).Существует объем тела (V)).

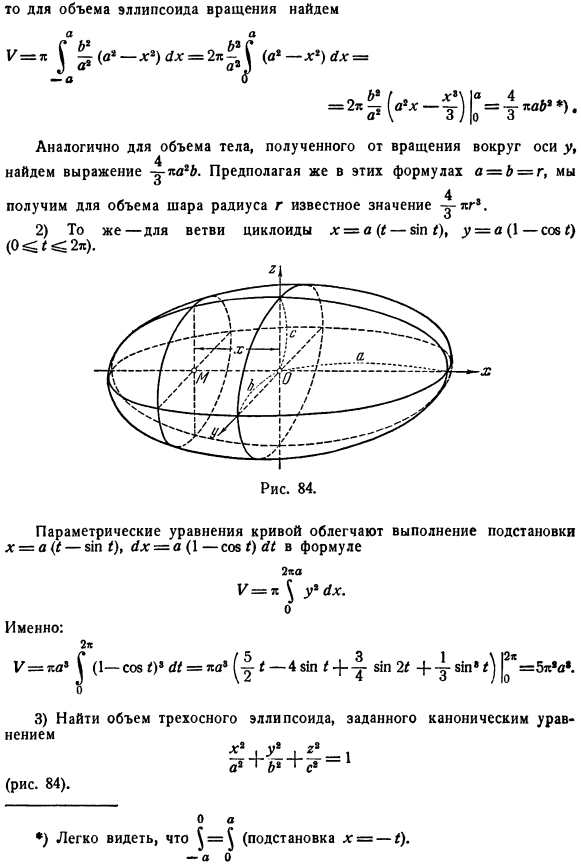
Важным частным случаем, в котором явно выполняются приведенные выше предположения о взаимном расположении секций, является вращающееся тело. представьте себе кривую, заданную в уравнении y = f (x) (a ^ x ^ b), в плоскости xy. Где f (x) является непрерывным и неотрицательным. начните вращение трапеции, центрированной по оси x и окруженной ею (рис. 83, а и Б).Полученное тело (V) четко соответствует рассматриваемому случаю, поскольку его сечения проецируются в плоскости, перпендикулярной оси x, в виде концентрических окружностей. Здесь. Р(х)= т ^ = б {ф(х）\ Как это (9 )） Г-ух МС = МС $ | / ( * )] в УГ. Если криволинейная трапеция окружена кривой V \ = f (x) и y% = fa (x) снизу и сверху、 У = К \ Х-У] {[/, Х*)] 9 [/, МП о, (10） Но、 * ) .

Например, если разделить промежуток на равные части, то можно легко различить последовательность входящих и исходящих тел, упомянутых в процитированном предложении. Однако частичные предположения не удовлетворяются here. In В общем случае можно утверждать только следующее: тело (если имеется объем*в 10) представлено формулой (8). Пример 1) поверните эллипс вокруг оси x с помощью+ + ^ = 1. Так, например, если тело удовлетворяет условиям теоремы 3\, то объем сфероида равен (в * —л:*) ых = Аналогично находим формулу—kab для объема объекта, полученного при вращении вокруг оси Y.

В общем, доказанный результат легко распространяется на все тела, которые получены путем сложения или вычитания из тел, удовлетворяющих вышеуказанным предположениям. Людмила Фирмаль

Предполагая, что эти выражения= = = r、 Получает известное значение объема шара радиуса Р 2) ветвление циклоиды x = o {1-an/), y = a (\soe /） (0 ^ / 2π). Параметрическое уравнение кривой облегчает подстановку x = a (I-$ w/), 4x = a (\soy/) 41. То есть： 2л ^(1 — а/) * Д1-ба%^ /-4 КТ / 4 «2 / ±| −5м * / ^ | ^ * = 5Т * м#. О 3) найти объем трехосного эллипсоида, заданный каноническим уравнением * * 1 2 * А * Б * * ые * (84). Да. * ) $ = $(Заменить x= -/) легко увидеть. И, ЭМ… Y * (*=СОП $ 1). плоскость, перпендикулярная оси x, проходя через точку M (x) на этой оси, пересекает эллипсоид эллипса. Уравнение для проецирования на плоскость yy (без искажения) выглядит следующим образом: Из этого видно, что его полуоси соответственно равны, а площадь (n * 196, 1)] представлена следующим образом: Таким образом, по формуле (8), искомый объем Но… В = ^(А8 -) топор = па. ля 4) оси.

Выражение площади интегралом.	Определение понятия длины дуги.
Определение понятия объема, его свойства.	Длина дуги. Леммы.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.