Оглавление:
Выпуклость и вогнутость графика функции, точки перегиба
Пусть функция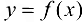 
задана па интервале 
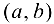, непрерывна на этом интервале и в каждой точке графика этой функции существует единственная касательная.
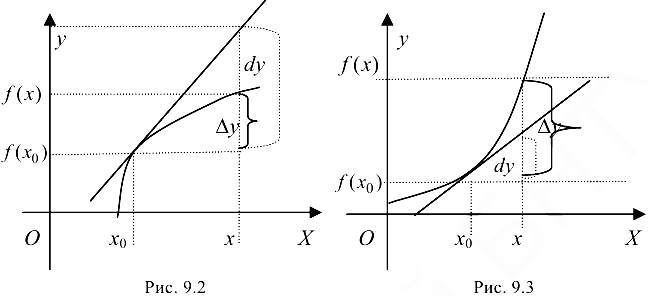
Определение 9.1. График функции 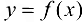называется выпуклым или выпуклым вверх па интервале 
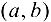, если он расположен ниже любой своей касательной, т. е. 
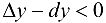(рис. 9.2); график функции 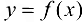называется вогнутым или выпуклым вниз на интервале 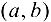, если он расположен выше любой своей касательной, т. е. 
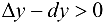(рис. 9.3).
Определение 9.2. Точки графика функции, в которых выпуклость сменяется вогнутостью или наоборот, называются точками перегиба графика.
Теорема 9.4. Пусть функция 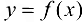определена и дважды дифференцируема на интервале 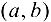. Тогда если 
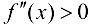для 
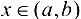, то на этом интервале график функции вогнутый; если 
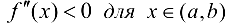, то на этом интервале график функции выпуклый.
Доказательство.
Рассмотрим разность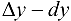 
на отрезке 
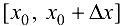, если 
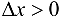, и на отрезке 
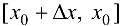, если 
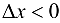. Согласно теореме 7.4 (Лагранжа):
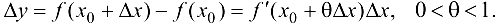
Поэтому
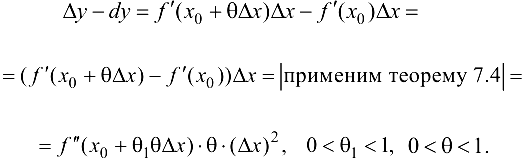
Тогда, при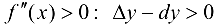 
, следовательно на этом отрезке график функции будет вогнутый; при 
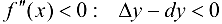, следовательно на этом отрезке график функции будет выпуклый. ■
Теорема 9.5 (необходимое условие точки перегиба). Пусть график функции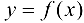 
имеет перегиб в точке 
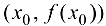и пусть функция 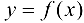имеет в точке 
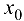непрерывную вторую производную. Тогда 
.
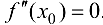Доказательство.
Пусть 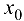— абсцисса точки перегиба графика функции 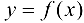. Для определенности будем считать, что выпуклость сменяется вогнутостью, т. е. при 
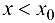справедливо неравенство 
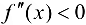, при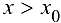 
справедливо неравенство 
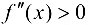. Тогда 
, 
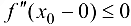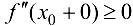. Так как, по условию теоремы, вторая производная в точке 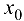существует, то 
. ■
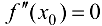Определение 9.3. Точка 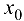из области определения функции 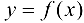называется критической (стационарной) точкой второго рода, если вторая производная функции в этой точке обращается в пуль 
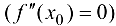или не существует.
Замечание 9.3. Не всякая точка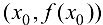 
, для которой 
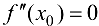является точкой перегиба.
Пример 9.4.
График функции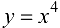 
не имеет перегиба в точке (0; 0), хотя 
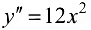обращается в 0 при 
.
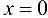Теорема 9.6 (достаточное условие точки перегиба). Пусть функция 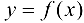определена и дважды дифференцируема в некоторой окрестности точки 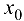. Тогда если в пределах указанной окрестности 
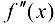имеет разные знаки слева и справа от точки 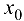, то график функции 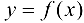имеет перегиб в точке 
.
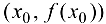Доказательство.
Из того, что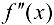 
слева и справа от точки 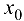имеет разные знаки, на основании теоремы 9.4 можно сделать заключение, что направление выпуклости графика функции слева и справа от точки 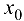является различным. Это и означает наличие перегиба в точке 
. ■
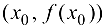Замечание 9.4. Теорема остается верной, если функция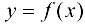 
имеет вторую производную в некоторой окрестности точки 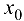и существует касательная к графику функции в точке 
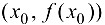. Тогда если в пределах указанной окрестности 
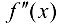имеет разные знаки справа и слева от точки 
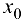, то график функции 
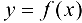имеет перегиб в точке 
.
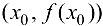Пример 9.5.
Точка (0; 0) является точкой перегиба графика функции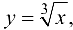 
, хотя вторая производная функции при 
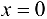не существует. Касательная к графику функции 
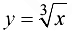в точке (0; 0) совпадает с осью 
.
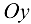Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
