Задача №123.
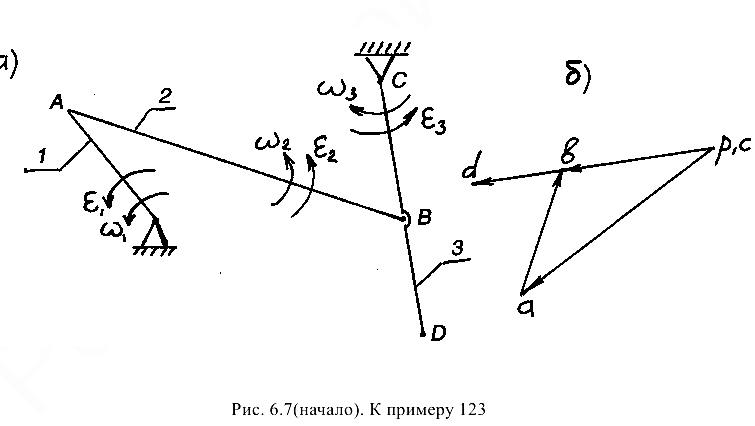
Выполнить кинематический анализ рычажного механизма, представленного на рис. 6.7, а. Построить планы скоростей механизма для двух положений и для одного положения план ускорений.
Размеры звеньев:
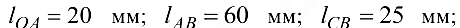
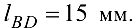
Угловая скорость кривошипа 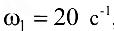 , а ускорение
, а ускорение 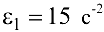 .
.
Решение:
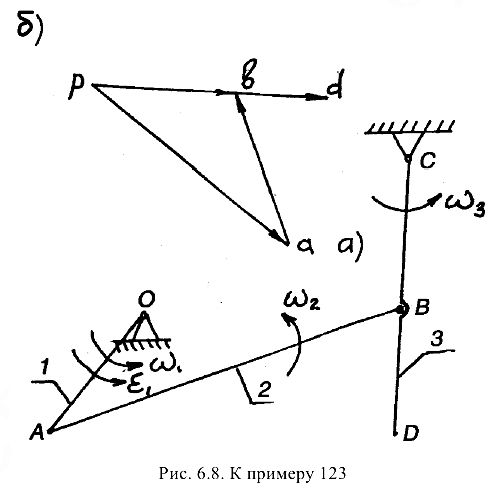
- Положения механизма, для которых будем строить планы скоростей, представлены на рис. 6.7, а и 6.8, а.
- Построение плана скоростей для параллельного положения механизма (рис. 6.7, а).
Скорость точки 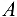 начального звена
начального звена
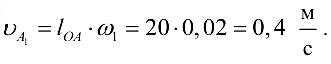
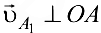 и направлена в сторону
и направлена в сторону 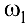 .
.
Выбираем масштабный коэффициент
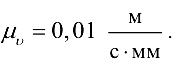
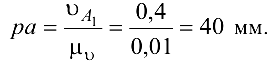
Для определения скорости точки 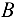 рассмотрим структурную группу (2,3).
рассмотрим структурную группу (2,3).
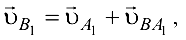
при этом
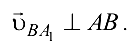
С другой стороны,
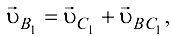
причём
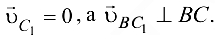
Решая два последних уравнения графически, найдём точку 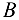 :
:
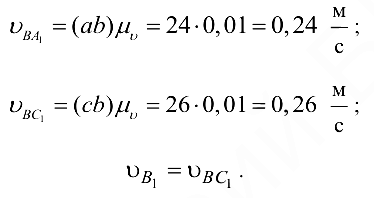
Скорость точки 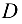 найдём на основании теоремы подобия:
найдём на основании теоремы подобия:
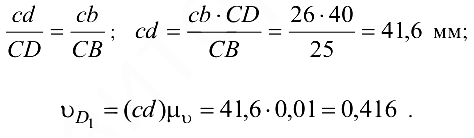
Угловая скорость звена 2:
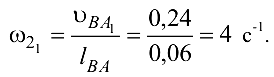
Угловая скорость звена 3:
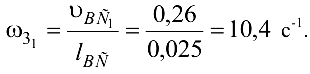
Для определения направления угловых скоростей 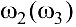 переносим векторы относительной скорости
переносим векторы относительной скорости 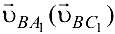 в точку
в точку 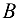 и наблюдаем, в какую сторону
и наблюдаем, в какую сторону 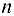 поворачивает звено 2(3) относительно точки
поворачивает звено 2(3) относительно точки 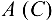 .
.
Построенный план скоростей представлен на рис. 6.7, б. Для построения плана скоростей для 2-го положения механизма (рис. 6.8, а) воспользуемся теми же формулами:
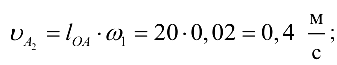
масштабный коэффициент скоростей
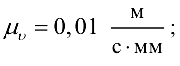
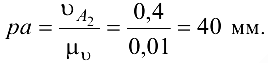
Скорости 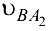 и
и 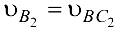 найдём, как и раньше, из графического решения аналогичных уравнений.
найдём, как и раньше, из графического решения аналогичных уравнений.
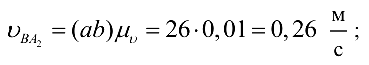
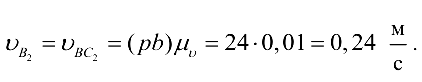
Скорость точки  найдём, используя теорему подобия:
найдём, используя теорему подобия:
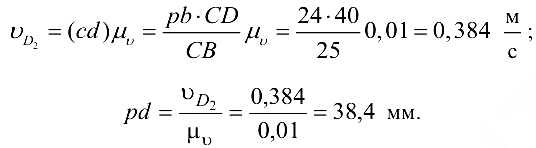
Угловые скорости звеньев:
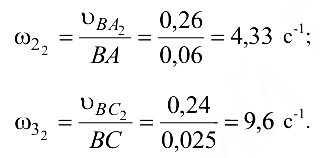
Направление угловых скоростей определяется аналогично. Искомая схема скоростей представлена на рис. 6.8, б.
- Для построения плана ускорений воспользуемся 1-м положением механизма (см. рис. 6.7, а). Ускорение точки
 начального звена
начального звена
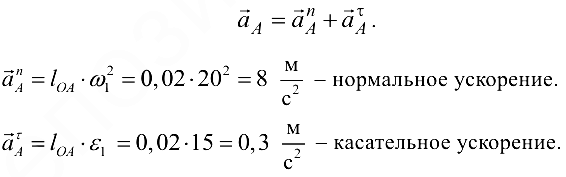
Причём 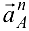 направлено вдоль
направлено вдоль 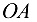 от
от 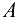 к
к  , а
, а 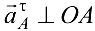 в сторону
в сторону 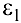 .
.
Масштабный коэффициент ускорений выбираем равным
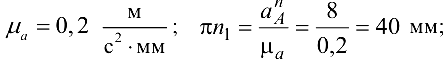
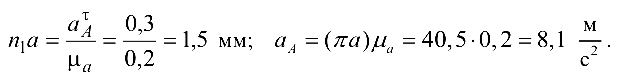
Ускорение точки 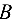 найдём на основании теоремы о сложении ускорений в сложном движении:
найдём на основании теоремы о сложении ускорений в сложном движении:
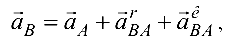
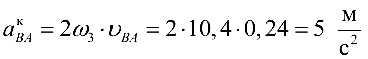
кориолисово ускорение.
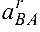 — относительное ускорение;
— относительное ускорение; 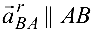 .
.
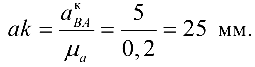
Кроме того,
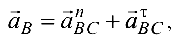
где
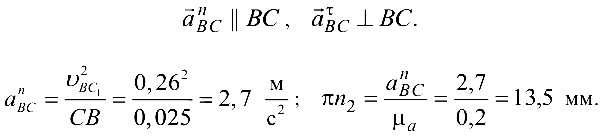
В результате совместного графического решения двух уравнений, составленных для нахождения ускорения точки 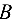 , получаем
, получаем
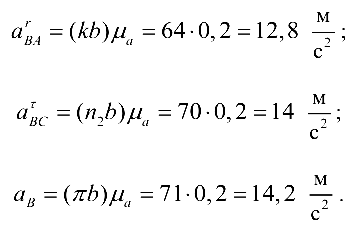
Ускорение точки 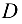 определяем на основании теоремы подобия:
определяем на основании теоремы подобия:
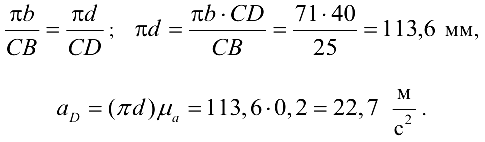
Угловые ускорения звеньев 2 и 3 соответственно
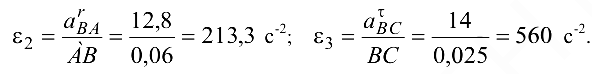
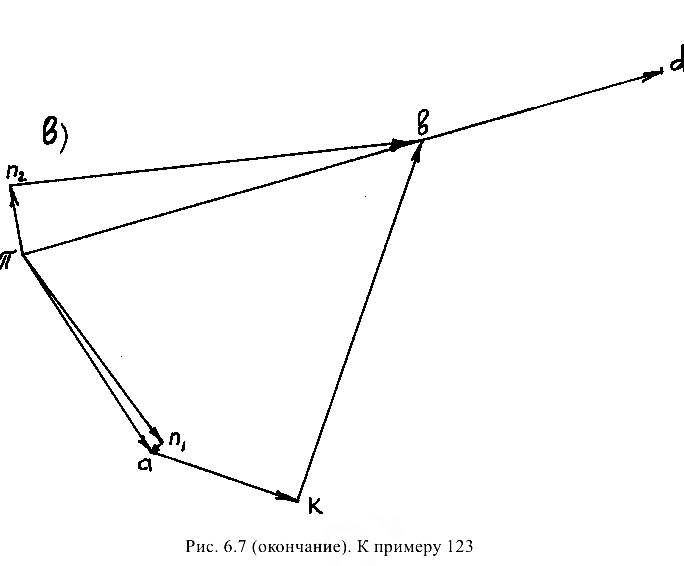
Искомый план ускорений представлен на рис. 6.7, в.
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

