Вычисление производной алгебраической суммы, произведения и частного функций

Вычисление производной алгебраической суммы, произведения и частного функций

Теорема 5.2. Если функции 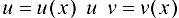дифференцируемы в точке 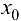, то функции 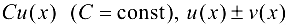, 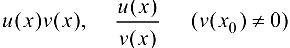также дифференцируемы в этой точке, причем:

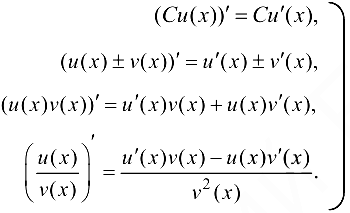
(5.3) — основные формулы дифференцирования.

Доказательство. Докажем первые три формулы.

1. Рассмотрим функцию 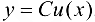. Тогда ,

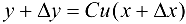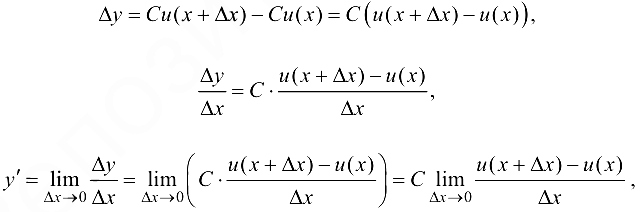
т. е. .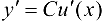

2. Рассмотрим функцию 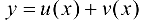. Тогда

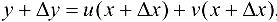
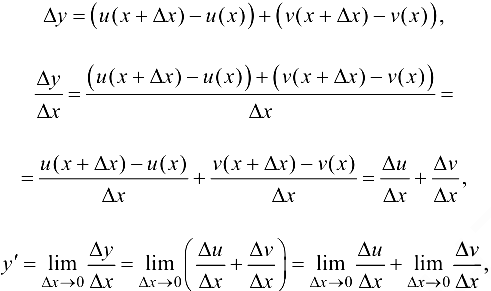
т. e. 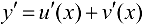. Случай 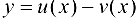доказывается аналогично.

3. Рассмотрим функцию 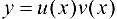. Тогда

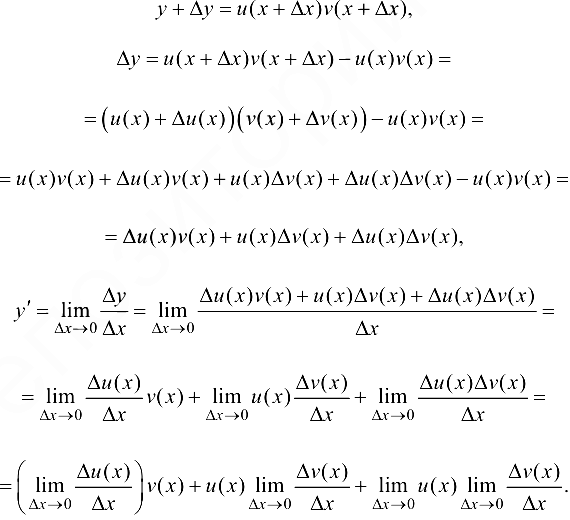
Рассмотрим последний член в правой части формулы: 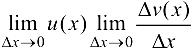. Так как 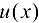— дифференцируемая функция, то она непрерывна. Следовательно, 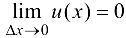, , 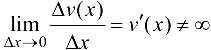так как 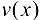— дифференцируемая функция,

Таким образом, рассматриваемый член равен нулю, и окончательно получаем: ■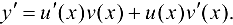

Пример 5.2.

Найти производную функции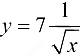

Решение:

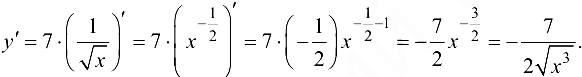
Ответ: .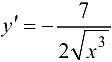

Пример 5.3.

Найти производную функции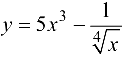

Решение:

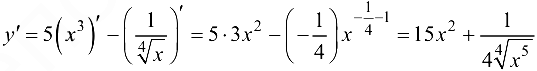
Ответ: .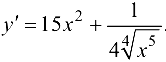

Пример 5.4.

Найти производную функции .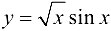

Решение:

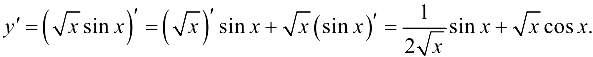
Ответ: .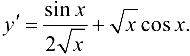

Пример 5.5.

Найти производную функции .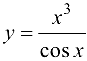

Решение:

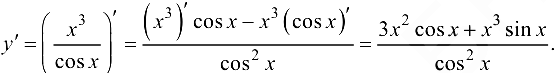
Ответ: .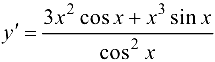

Эта лекция взята со страницы лекций по предмету математический анализ:

Предмет математический анализ

Возможно вам будут полезны эти страницы:

Физический смысл производной функции: вывод

Непрерывность функции, имеющей производную с примером решения, таблица производных и правила дифференцирования

Производная сложной функции с примерами решения

Производная обратной функции с примерами решения