Оглавление:
При вычислении пределов, содержащих тригонометрические функции, в зависимости от вида функции используют либо тригонометрические формулы, либо первый замечательный предел, либо эквивалентность бесконечно малых, либо правило Лопиталя, либо делают замену переменных.
Пример №1.
Вычислить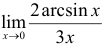 
.
Решение:
Рассмотрим два способа решения.
1. С помощью замены:
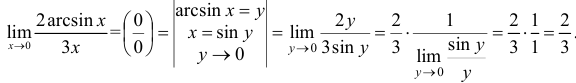
2. Использование эквивалентности бесконечно малых:
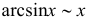при 
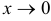, следовательно,
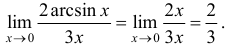
Пример №2.
Вычислить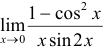 
.
Решение:
Воспользуемся основным тригонометрическим тождеством и формулой синуса двойного угла, а потом первым замечательным пределом:
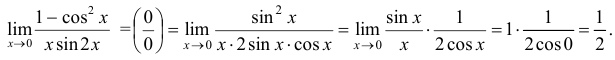
Пример №3.
Вычислить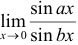 
, где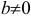 
.
Решение:
Воспользуемся правилом Лопиталя:
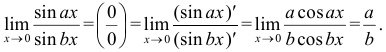
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Вычисление пределов от рациональной дроби при x > ∞ |
| Вычисление пределов, содержащих радикалы |
| Вычисление пределов от показательно-степенных функций |
| Вычисление пределов с учетом их особенностей |
