Свойства определенного интеграла доказываются на основе его определения (7.2), а также могут быть объяснены с помощью геометрического смысла.
1. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.
2. Постоянный множитель выносится за знак интеграла.
3. При перестановке пределов интегрирования знак интеграла меняется на противоположный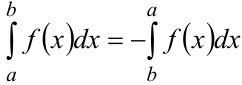 
.
4. Интеграл с одинаковыми пределами интегрирования равен нулю, что можно объяснить как следствие предыдущего свойства: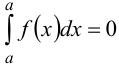 
.
5. Для произвольного расположения точек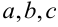 
на числовой оси справедливо равенство 
.
6. Интеграл от знакопостоянной функции есть число того же знака, что и функция: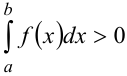 
, если 
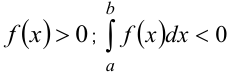, если 
.
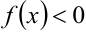7. Абсолютная величина интеграла не превосходит интеграла от абсолютной величины функции: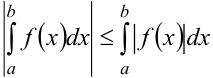 
.
8. Определённый интеграл не зависит от переменной интегрирования:
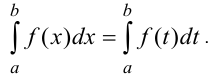
9. Оценка определенного интеграла. Если функция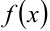 
непрерывная на отрезке 
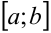и имеет на нем наименьшее и наибольшее значения, равные 
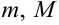, то значение интеграла можно оценить по формуле:
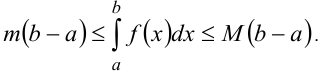
10. Если подынтегральная функция — непрерывная, то внутри отрезка интегрирования 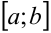существует хотя бы одна точка 
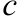, такая, что значение функции в ней, умноженное на длину отрезка интегрирования, равно определённому интегралу (теорема о среднем).
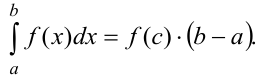
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
