Оглавление:


Возрастание (убывание) функции в точке. Локальный экстремум
- Увеличение (уменьшение) функции в это время. Локальный экстремум Рассмотрим функцию y=/(x), определенную в любом месте окрестности неподвижной точки C. О П Р Е Д Е Л Е Н и Е1. Например, предположим, что в функции y=(x) Zr A C A t t T T T T T o h K e s, Если существует 8 окрестностей точки C, то в ней есть xx>C в (C). О П Р Е Д Е Л Е Н и Е2. Если существует 8 соседей таких точек C, то мы говорим,
что функция y=/(x) y b s является e t из t o h K e s ?(х)>?(C)при Х<с ■С /(х)С. О П Р Е Д Е Л Е Н и Е3. Допустим, функция y=?(икс).Если существует 8 соседей точки C, то значение [(C) является наибольшим[минимальным] среди всех значений/(x) этой функции. О П Р Е Д Е Л Е Н И Е 4. Допустим, функция y=?(x) если эта функция имеет либо локальное максимальное значение, либо локальное минимальное значение в указанной точке, то используется точка
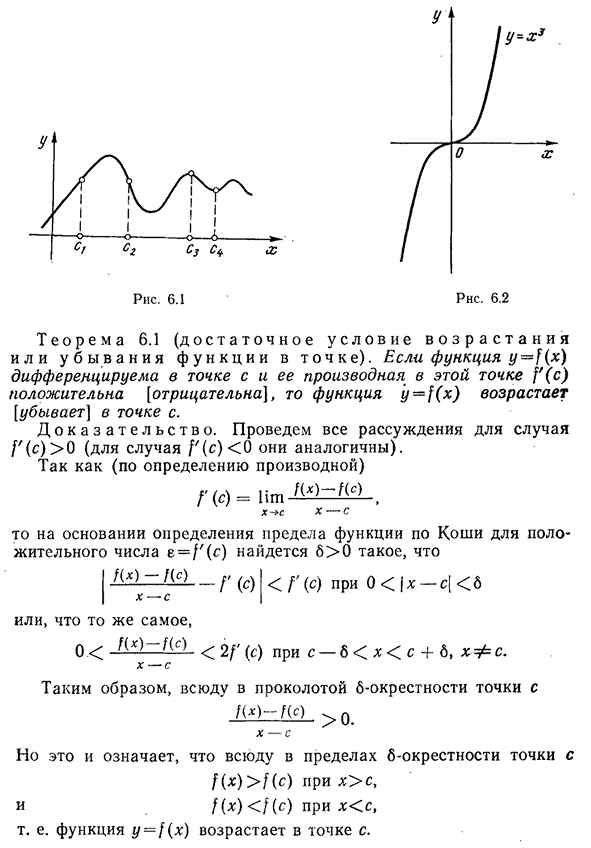
C l o K a l n y e K t R e m y m y m m. Для риса. 6.1 я показываю функцию увеличения в точке C для уменьшения в точке SG, имеющую Людмила Фирмаль
локальное максимальное значение в точке SZ.И локальный минимум С4. Доказываются следующие две теоремы.§1. Локальный экстремум 225 6.1 (KC I i или U b s A n I или U b s A N I F I K I в пунктах). Если функция y-CX) дифференцируема в точке C, и эта точка [‘(C) положительна[отрицательна], то функция y=1 (x) увеличивается[уменьшается]в точке C. Д О К а з а т е л ь с т в о. сделаем все аргументы в случае D(C)>0(случай/'(C)<0 они похожи).
Так как (по определению производная)/'(C)=11T X-C Тогда, исходя из определения пределов функции Коши для положительного числа e= / ‘(C), существует 6>0, например:/(■^) — Ls) — — — — — I<at o< / x-s / <6 Х-З. Или, что то же самое, о<2/'(C)C-6<x<C+6, x C. Х-З. Таким образом, точка C/(x) — в любом месте панк — 6 окрестности DS) Х-ы Но это также означает, что в любом месте из 6 соседних точек C/(x)/(C) и (C) x<C), т. е. функция y=/(x), будет увеличиваться в точке C. Зак 72226 Глава 6. Основная
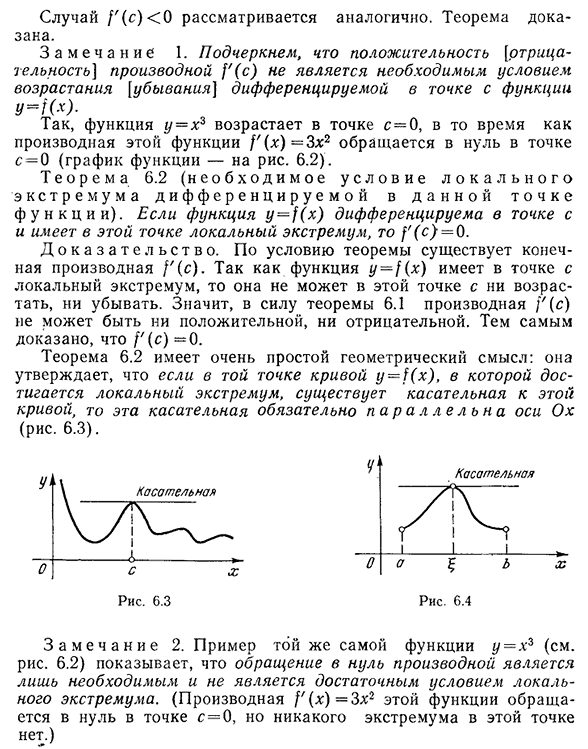
- теорема о дифференцируемых функциях Случай D (C)<0 рассматривается аналогичным образом. Теорема доказана. З а м е ч а н и Е1. Таким образом,функция y=X3 возрастает в точке C=0, а производная этой функции [‘(x)—3×2 исчезает в точке C=0(график функции—фиг. 6.2). 6.2 (Н ЕО б х О Д и М О У С Л О В и Е Л О Г О Э К С Т Р Е М А Д и Ф Е Р Е Н Ц и Р М О й В Д А Н Н О Й Т О Ч функция y=1 (х) Д О К а з а т е л ь с т в о. По условиям теоремы, существует конечная производная/'(с). Поскольку функция y=/(x) имеет локальное
экстремальное значение в точке C, то в этой точке C она не увеличивается и не уменьшается, следовательно, согласно теореме 6.1 производная/'(C) не является ни положительной, ни отрицательной. Таким образом, доказано, что/'(C)=0. Теорема 6. 2 имеет очень простое геометрическое значение:это точка кривой y=f (x), которая достигает локального экстремума, если есть касательная к этой кривой,
то эта касательная обязательно равна 6.3). З а м е ч а н и Е2. Пример такой Людмила Фирмаль
же функции y=X3 (см. рисунок). 6.2) указывает на то, что исчезновение производной не является достаточным условием для локальных экстремумов, а лишь необходимым условием. (Производная этой функции/'(x)=3×2 исчезает при C=0, но экстремумов в этой точке нет.)
Смотрите также:

