Возрастание и убывание функции
Функция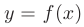 
называется неубывающей (или невозрастающей) на интервале 
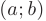, если для любых 
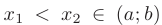верно неравенство 
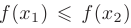(или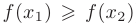 
). Интервалы из области определения функции 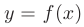, на которых функция неубывает (или невозрастает) называются интервалами монотонности этой функции.
Необходимое условие монотонности. Если дифференцируемая на некотором интервале 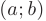функция 
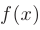не убывает (не возрастает), то ее производная для любого 
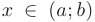будет неотрицательна 
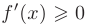(неположительна 
).
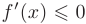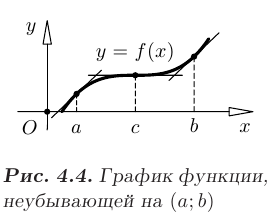
Геометрически это означает, что касательные к графику неубывающей дифференцируемой функции образуют острые углы с положительным направлением оси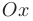 
или параллельны ей (см. рис. 4.4). Тогда касательные к графику невозрастающей дифференцируемой функции образуют тупые углы с положительным направлением оси 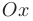или параллельны ей.
Достаточное условие монотонности. Если функция 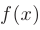дифференцируема на некотором интервале 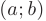и для любого 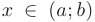ее производная будет неотрицательна 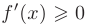(неположительна 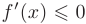), то функция 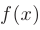не убывает (не возрастает) на этом интервале.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Теоремы о дифференцируемых функциях в математике |
| Правило Лопиталя в математике |
| Максимум и минимум функции в математике |
| Наибольшее и наименьшее значение функции на отрезке в математике |
