Оглавление:




Внутренние силы. метод сечений. эпюры
- Внутренняя сила. Метод сечения. Фигура Между соседними частицами тела (кристаллами, молекулами, атомами) всегда существует определенная сила взаимодействия. Во всех случаях эти силы противодействовали любым попыткам сохранить его в целом Рис тринадцать Изменяют относительное положение частиц, то есть деформируют тело. Внешние силы, наоборот, всегда стремятся
вызвать деформацию тела, чтобы изменить взаимное расположение частиц. Поэтому величина внутренних сил, действующих между любыми двумя частицами в нагруженном ненагруженном теле, будет различной. Поэтому в дальнейшем, в результате нагружения тела, необходимо учитывать внутренние силы, действующие на
тело, которые находятся в его естественном (ненагруженном) состоянии Людмила Фирмаль
и учитывать силы дополнительного взаимодействия, возникающие в результате нагружения, говоря о внутренних силах. 内部力はしばしば次のように呼ばれますeffort. To для определения и расчета внутренних сил сопротивления материала широко используется метод поперечного сечения. Рассмотрим любое тело, оснащенное
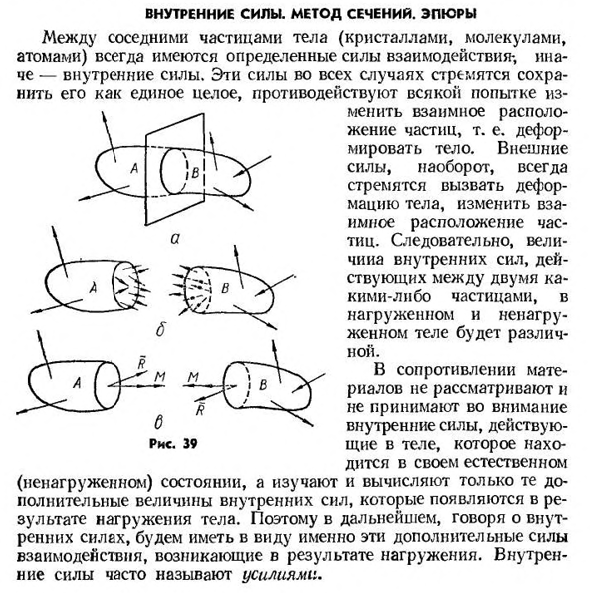
самобалансирующейся системой сил. В интересующих нас местах мысленно рассекают его несколько плоскостей на две части-А и Б (рис. 39, а). В этом случае в самой секции есть те, которые принадлежат части A(слева) тела, и те, которые принадлежат части B (справа). Действуют силы взаимодействия в каждой точке с обеих сторон поперечного сечения (рис. 39, б). На основании этой
- гипотезы И противоположное направление Что касается сплошности материала, то следует предположить, что внутренняя сила действует на все точки сечения, а следовательно, представляет собой распределенную нагрузку. В зависимости от формы тела и характера приложенных внешних нагрузок, сила внутренних сил в разных точках может отличаться. Согласно третьему закону Ньютона, внутренняя сила, действующая на часть, принадлежащую части тела A, равна внутренней силе, действующей на часть, принадлежащую части тела B (39, b). Другими словами,
взаимодействуют внутренние силы, действующие на разные части тела. Как и в любой системе сил, их можно свести в одну точку (обычно к центру тяжести секции), и в результате на каждой стороне секции, секции 39, б). Стержень, в частности, обычно рассекается плоскостью, перпендикулярной оси, то есть поперечным сечением(рис. 40, а). Если главные моменты основного вектора и внутренние силы проецируются на главную ось стержней x-axis и на главную ось сечений y и z, то на каждой стороне сечения 40, b) получают шесть коэффициентов внутренних сил: три-силы
(N, Qf/, Q2) и три-моменты (L4J, L4u и L4g). Эти величины называются Людмила Фирмаль
внутренними силами в поперечном сечении стержня. Сила L / вызывает продольную деформацию (растяжение или сжатие) стержня; Qy и Qz-смещение сторон сечения соответственно в направлении оси y и 2;MX-для силы и момента в сечении, следовательно, приняты следующие обозначения: N-продольное или осевое (в сторону оси стержня); qz-поперечное направление (редко Для силы и момента в сечении можно дать следующее определение: вертикальная сила N действует на Нормаль (или ось стержня) сечения, в пределах которой все сечения y и z для главной центральной оси. Каждая из этих сил или моментов, как уже
указывалось, является результатом взаимодействия рассеченных частей тела, и, следовательно, 40, б), хотя и в противоположном направлении. Набор значений N, Q,., Qz и др. Применяется к правой стороне секции, заменяет дистанционное действие на левой стороне штанги на правой стороне; применяется к левой стороне секции сила и крутящий момент, установленный применяется к правой стороне штанги.、 Равна алгебраической » сумме проекций на ось стержня(перпендикулярно поперечному сечению) всех внешних сил, действующих на одну сторону (левую или правую)разделенного стержня; Qv-то же самое, но на ось y; Qz-то же самое; mu-ось y, m g-
то же самое, но ось g-то же самое. К такому выводу легко прийти, рассматривая равновесие каждой части рассеченного стержня. В этом случае сумма проекций (или моментов) сил, расположенных на левой стороне сечения, должна быть приложена к правой стороне сечения, и наоборот. Таким образом, в методе сечения можно найти все силы и моменты любого сечения стержня под действием любой нагрузки. Для этого: 1) Найдите главную центральную ось области сечения;2)мысленно нарисуйте поперечное сечение стержня в том месте, где вы хотите найти силу и момент; 3)нарисуйте силу D, Qy, Qz и момент. Для примера применения метода 38 сечений
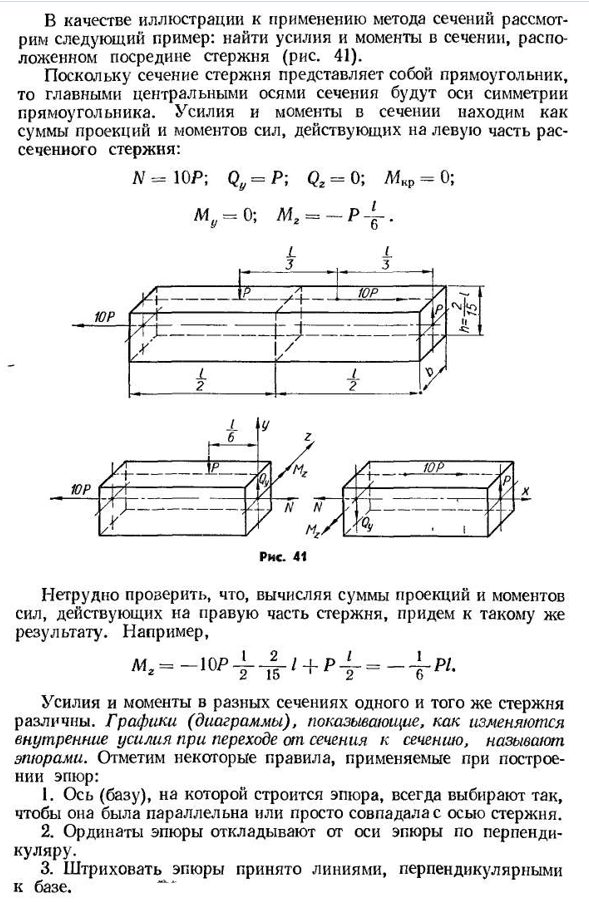
рассмотрим следующий пример: найти силу и момент сечения в середине стержня (рис. 41). Поскольку сечение стержня прямоугольное, главной центральной осью сечения будет ось симметрии прямоугольника. Сила и момент сечения определяются как сумма проекции и момента силы, действующей на левую сторону рассеченного стержня: L’ — Yu P;<^=P; (?г=0;МД=0;Л^=0;= Один. Л Райс, сорок один. Нетрудно заметить, что если рассчитать сумму момента и предсказать силу, действующую на правую сторону стержня, то получится тот же результат. Например, M «= — / 0P4 4’+p4 — = — 4pz-
Силы и моменты различных сечений одного и того же стержня различны. График (рисунок), показывающий, как изменяются внутренние силы при переходе от секции к секции. Обратите внимание на некоторые правила, используемые в сюжете: 1. Ось (основание), на которой построен участок, всегда выбирается параллельной или просто совпадающей с осью стержня. 2. Вертикальная ось участка расположена вертикально от оси участка. 3. Заговор перпендикулярен линии. 394 усилие и выбрать какой-то масштаб на данный момент. Координаты строго определены в масштабе. Кроме того, на графике мы ставим цифру, указывающую величину характерных координат, а в поле графика по кругу отмечаем усилие.
Смотрите также:
| Основы расчета балок на упругом основании | Эпюры продольных сил |
| Напряжения и деформации в винтовых пружинах с малым шагом | Эпюры крутящих моментов |

