Вихревые линии и трубки. Теорема Гельмгольца. Образование вихрей.

Вихревые линии и трубки. Теорема Гельмгольца. Образование вихрей.

Вихревые линии и трубки. Теорема Гельмгольца. Образование вихрей. Рассмотрим случай, когда вектор а отличается от нуля в каждой точке пространства, занятого движущейся жидкостью, то есть все частицы вращаются. Вы можете создать векторные линии поля с вектором сотрудничества. Теперь назовем кривую в каждой точке, где вектор co направлен вдоль тангенциального вихря line. In в свою очередь, основной отрезок такой линии(рис.2.11) служит мгновенной осью вращения находящихся на ней частиц жидкости. Очевидно, что это движение возможно только при деформации вращающихся частиц жидкости.

Это происходит потому, что, вообще говоря, вихревые линии изогнуты и вообще не могут функционировать как ось вращения жидкости конечного объема. Дифференциальное уравнение вихревой линии легко получить из ковариации векторов угловой скорости σ (σ, ω, ω, ω) и основных направленных сегментов дуги вихревых линий (yx, yy, yy).Форма пропорционального условия проекции одноименных этих векторов имеет вид s1x / гг = гг / гг = ее / Г *. (2.34） Зная функции ω*(x, y, r), wn(x, y, r) и ω*(x, y, r), можно найти расположение вихревых линий из 2 систем уравнений (2.34).

Нарисуйте линию вихря через точки небольшого замкнутого контура Н1(рис. 2.12).Полученная трубообразная поверхность называется основной вихревой трубой, а множество частиц, окруженных ею, называется вихревой нитью. Людмила Фирмаль

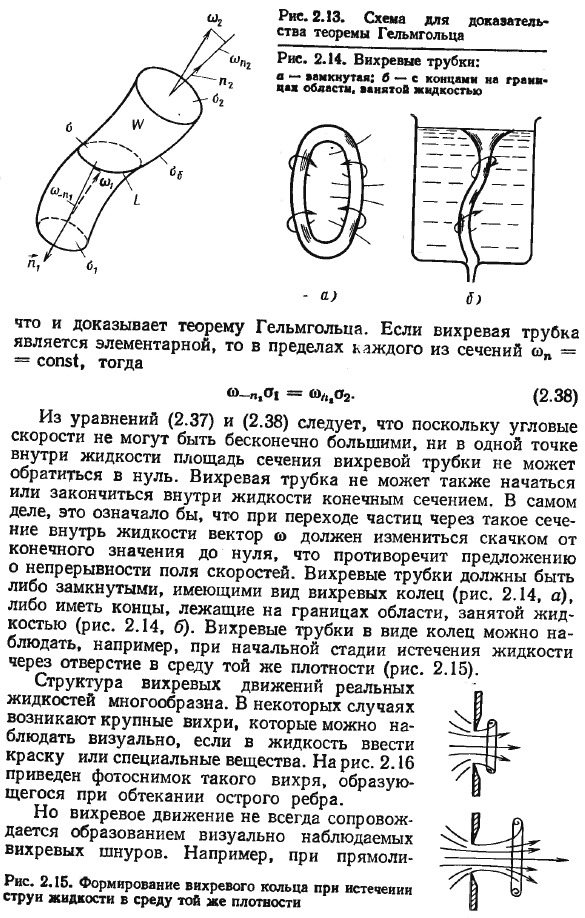
• Если поперечное сечение вихревой нити достаточно мало, то можно считать, что вектор ω имеет внутри нее постоянную величину. Скалярное произведение векторов co и yo называется интенсивностью или интенсивностью вихревой трубы и действует как мера вихревого движения. э?/ = СО-с & м =&n01a (2.35） Сорок три Возьмите любую поверхность o, где она Основная область Yo, мы строим вихревую трубу в каждом из них. Суммарная прочность этих трубок равна потоку вектора©через поверхность. / = Я© «йог = / ©» Эй. (2.36） О, да. Значение 2 / −21©n yo■ * / 0 ″ yo-это post-st Вихревой вектор O течет через поверхность o, или просто вихревой поток. Построение вихревой линии через точку произвольного замкнутого контура Г вводит понятие конечной вихревой трубы (рис.2.13).В поперечном сечении такой конечной трубы вектор ω обычно является переменным.

• Докажите теорему Гельмгольца. Вихревой поток, проходящий через поперечное сечение вихревой трубы в данный момент времени, постоянен по ее длине. Сторону оси вихревой трубы и ее 2 поперечных сечения O, выбираем объем Ш7, ограниченный o. вихревой поток через поверхность 2-ax + o * + occ、 [©»е = | ©» е + | © «йоги 4 / ©» Эй. * °1°°б％ Поскольку вектор©тангенциально ориентирован к поверхности вихревой трубы, то на поверхности он равен a0 = 0.Таким образом, 2-й Интеграл справа от последнего уравнения будет равен нулю. Кроме того, по теореме Гаусса-острограцкого На поверхности oX мы заменяем нормальный lx на внутренний-px, учитывая, что он направлен наружу объема I7.Затем вы можете переписать последнюю связь как / © _ «йо = / ©» Эй,(2.37） Сорок четыре Ч%О Рисунок 213. 13схема для доказательства теоремы Гельмгольца Это доказывает теорему Гельмгольца. Если вихревая труба является основной, то в пределах каждого сечения » = = = const1 талантливый», 01 = ю/,, 02. (2.38） Из уравнений (2.37)и (2.38) следует, что угловая скорость не может быть бесконечно большой, поэтому площадь поперечного сечения вихревой трубы не исчезает ни в одной точке жидкости.

Вихревая труба не может также начать или закончить окончательное поперечное сечение внутри fluid. In Фактически это означает, что когда частица проходит через такое сечение и входит в жидкость, вектор w резко изменяется от конечного значения до нуля, что противоречит предположению о непрерывности поля скоростей. Людмила Фирмаль

• Вихревая труба либо замкнута в виде вихревого кольца(рис.2.14,а), либо имеет ребро на границе области, занимаемой жидкостью (рис. 2.14, б).Кольцевые вихревые трубки можно наблюдать на начальной стадии течения жидкости, например, из отверстия в среду той же плотности (рис.2.15). Структура вихревого движения реальной жидкости имеет вид diverse. In в некоторых случаях развиваются большие вихри, которые можно визуально наблюдать при введении в жидкость красок или специальных веществ. На рис. 2.16 показана фотография такого вихря, образовавшегося при обтекании острой реберной кости.

Однако вихревое движение не всегда сопровождается образованием вихревых нитей, которые визуально наблюдаемы. Например, простой Рисунок 2.15.Образование вихревых колец при протекании жидкости в среде одинаковой плотности Линейное перемещение вязкой жидкости между неподвижной и плоской параллельными стенками (рис. 2.17), проекция скорости в системе координат xy равна= /(y), u = = = 0, где f (y) непрерывная функция, согласно проекции вектора угловой скорости (2.30). 1 Дих 1 Д [» = 2-дю—2 ″ 〜 °ду -’ Вихрь, а вектор co во всех точках параллелен оси z (перпендикулярен плоскости.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Уравнение неразрывности в криволинейных ортогональных системах координат.
2. Общий характер движения жидкой частицы. теорема коши-гельмгольца.
3. Циркуляция скорости и теорема Стокса.
4. Безвихревое или потенциальное движение.