Векторы и операции над ними
Вектором называют направленный отрезок, соединяющий две точки и обозначают его как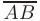 
или 
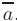. Точку 
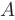называют началом, а точку 
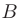— концом вектора .
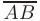Длина вектора соответствует расстоянию между его начальной и конечной точками и обозначается как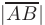 
. Вектор 
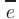называется единичным, если его длина равна единице в выбранной системе координат 
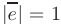. Длина нулевого вектора равна нулю 
.
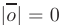Векторы называются коллинеарными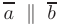 
, если они лежат на параллельных прямых. Векторы называются равными 
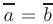если они имеют одинаковую длину и направление.
Компланарными называются векторы, лежащие в одной плоскости либо в параллельных плоскостях.
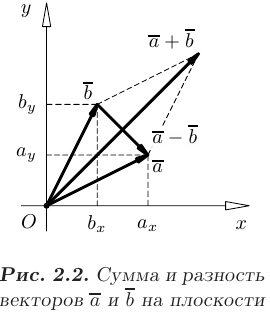
Суммой двух последовательно расположенных векторов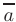 
и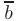 
называется вектор 
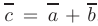, соединяющий начало первого вектора 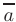с концом второго 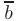(см. рис. 2.2). Для каждого вектора 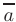существует противоположный вектор — 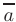такой, что 
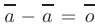. Тогда разностью двух векторов 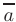и 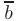называется вектор 
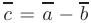такой, что 
.
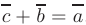Произведением вектора 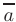на число 
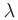называется вектор 
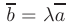, имеющий длину 
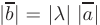, сонаправленный вектору а при 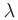> 0 и противоположно направленный при 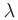< 0.
Заметим, что если вектор 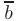коллинеарен ненулевому вектору 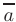, то существует действительное число 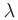такое, что 
.
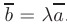Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
