Векторный вывод теоремы Кориолиса

Векторный вывод теоремы Кориолиса

Рассмотрим движение материальной точки М, положение которой относительно неподвижной системы координат Oxyz задается радиус-вектором R. Положение точки М относительно другой системы осей 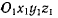движущейся относительно системы Oxyz, определим радиус-вектором r. Пусть, кроме того, Ro 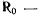радиус-вектор начала подвижной системы координат (рис. 70). Векторы 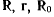связаны между собой геометрическим соотношением

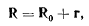
сохраняющимся в каждый момент времени. Скорость точки М относительно системы Oxyz определим, дифференцируя радиус-вектор R по времени

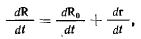
где производные как правой, так и левой части берутся в одной и
той же системе координат Oxyz. Радиус-вектор r, определяющий
положение точки М в системе 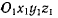можно представить в виде
суммы трех векторов:

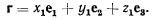
Тогда производная от вектора r в системе Oxyz получит вид

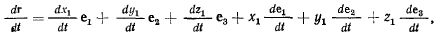
где производные 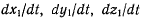являются проекциями относительной скорости точки М на оси подвижной системы, а производные 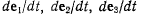определяются по формулам Эйлера

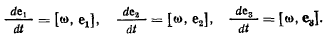
Поэтому для производной 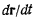будем иметь

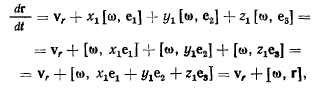
где

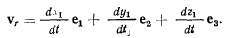
Обозначим через 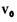скорость начала подвижной системы координат,
так что

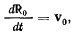
тогда формулу (b) можно будет переписать в виде

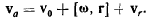
Обращаясь к теореме о сложении скоростей, получим выражение
для переносной скорости точки:

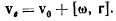
Вектор ускорения точки М получается в результате дифференцирования вектора ее скорости vo в системе Oxyz. Из равенства (с) находим

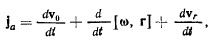
где первый член правой части 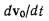представляет ускорение начала подвижной системы координат

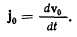
Дифференцирование векторного произведения дает

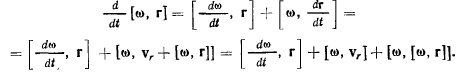
Наконец, дифференцирование вектора относительной скорости дает

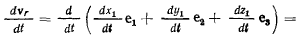
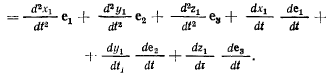
Величины 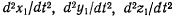представляют собой проекции относительного ускорения точки М на оси подвижной системы координат. Таким образом, вектор 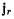относительного ускорения
точки М будет иметь вид

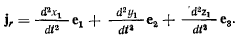
Для производной от вектора относительной скорости получим
выражение

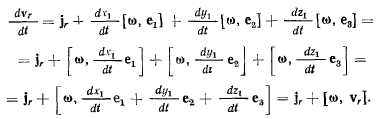
Окончательно равенство (d) приобретает теперь вид

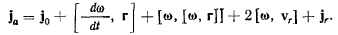
Переносное ускорение точки найдем, полагая, что точка не совершает движения относительно подвижной системы координат. В этом случае относительная скорость и относительное ускорение равны нулю, а потому будем иметь

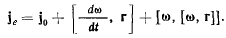
Обозначая через 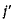векторное произведение

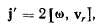
приходим к теореме Кориолиса

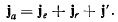
Замечание. Добавочное ускорение получается как за счет дифференцирования вектора относительной скорости в неподвижной системе координат, так и за счет дифференцирования вектора переносной скорости в той же неподвижной системе координат.

Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Ускорение точки в сложном движении

Замечание о дифференцировании единичного вектора

Теорема Ривальса

Распределение ускорений