Задача №103.
Вал со шкивом загружен в состоянии равновесия грузом 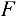 и силами
и силами 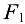 и
и 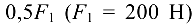 . Требуется определить реакции опор. Расположения шкивов и их диаметры:
. Требуется определить реакции опор. Расположения шкивов и их диаметры:
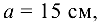
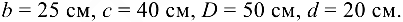
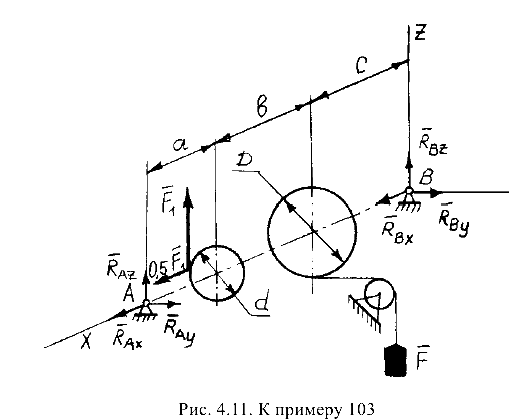
Прототипом примера является промежуточный вал зубчатых редукторов, применяемых в приводных станциях к сельскохозяйственным транспортёрам.
Решение:
Решим пример аналитическим способом на основе системы уравнений равновесия пространственной системы сил:
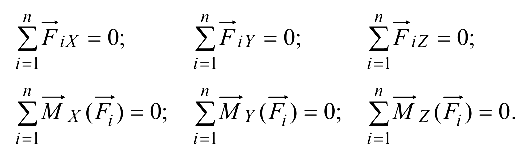
Применим эти уравнения к определению опорных реакций 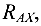
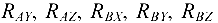 и уравновешивающей силы
и уравновешивающей силы 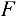 вала, несущего на себе два зубчатых колеса (или шкива) различных диаметров (рис. 4.11). Выбор системы координат показан на рис. 4.11. За ось
вала, несущего на себе два зубчатых колеса (или шкива) различных диаметров (рис. 4.11). Выбор системы координат показан на рис. 4.11. За ось 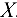 принимаем ось вала.
принимаем ось вала.
Уравнение моментов относительно оси вала
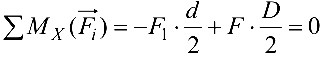
откуда
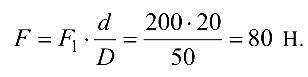
Уравнение моментов относительно горизонтальной координатной оси 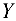
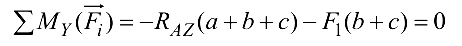
отсюда
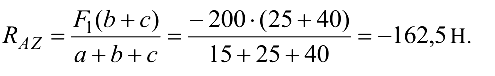
Уравнение моментов относительно вертикальной оси координат 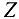
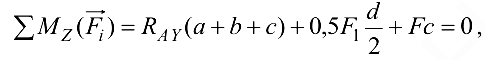
откуда
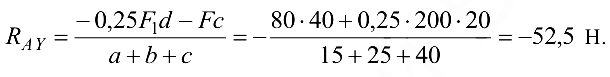
Для определения остальных неизвестных применим уравнения проекций сил на оси координат. Первое из них имеет вид
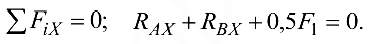
Чтобы определить каждую из неизвестных сил, необходимо принять во внимание, что подшипники валов в машинах устанавливаются обычно так, чтобы один из них, например 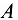 , допускал небольшое продольное смещение («люфт») и тем самым не оказывал сопротивления при давлении на него вдоль оси. В этом случае осевая реакция
, допускал небольшое продольное смещение («люфт») и тем самым не оказывал сопротивления при давлении на него вдоль оси. В этом случае осевая реакция 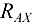 будет равна нулю, a
будет равна нулю, a
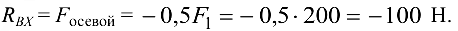
Второе уравнение проекций запишется следующим образом:
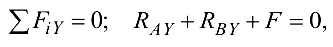
откуда
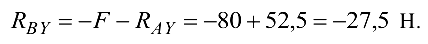
Третье уравнение
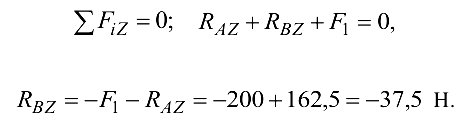
Полная реакция опоры 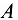
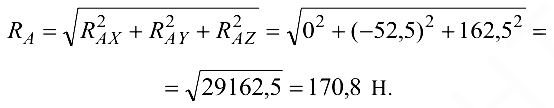
Полная реакция опоры 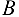
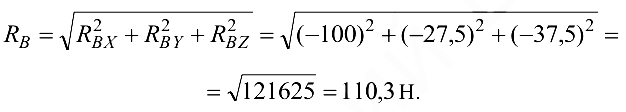
Ответ:
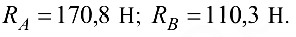
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

