Задача №62 с решением
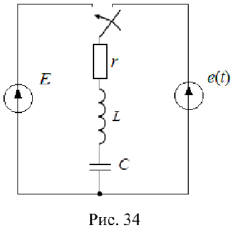
В схеме на рис. 34 происходит переключение ключа. Параметры схемы: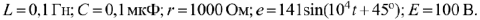 
. Рассчитать переходные процессы по току в индуктивности 
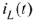и напряжению на ёмкости 
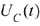в цепи.
Решение: Переходный процесс по току в индуктивности определим в виде
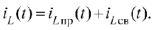
Так как после коммутации последовательная 
-цепь оказывается подключенной к источнику постоянного напряжения 
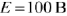, то принуждённая составляющая тока 
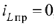,а напряжения — 
.
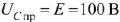Определим независимые начальные условия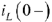 
и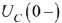 
, рассчитав предварительно комплексные амплитуды тока в индуктивности и напряжении на ёмкости в цепи до коммутации:
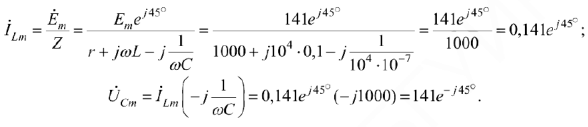
По найденным комплексным амплитудам запишем мгновенные значения тока в индуктивности и напряжения на ёмкости в цепи до коммутации:
Полагая в последних выражениях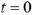 
— и учитывая законы коммутации, определим независимые начальные условия:
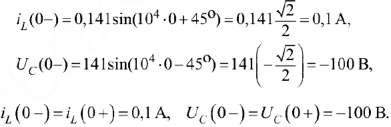
Характеристическое уравнения цепи будет иметь вид
После подстановки численных значений и приведения к виду с единичным коэффициентом при 
получим
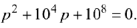
Решая полученное уравнения, находим его корни
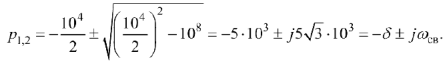
Переходный процесс по току в индуктивности определим как сумму принужденной и свободной составляющих:
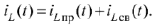
Так как корни характеристического уравнения получились комплексно-сопряженными, то свободную составляющую переходного процесса целесообразно искать в виде
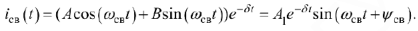
- В первом случае постоянные интегрирования —
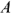и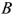 
, во втором случае — 
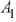и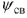 
. Воспользуемся первой формой и, учитывая, что 
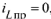., получим
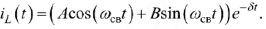
Для нахождения двух постоянных интегрирования необходимы два уравнения. Второе уравнение получим, взяв производную от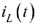 
:
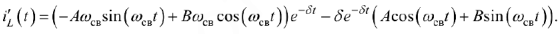
Полагая в обоих уравнениях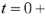 
, получим
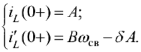
Необходимые зависимые начальные условия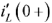 
получим из уравнения цепи после коммутации, записанного для момента времени :
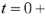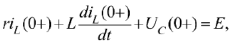
и с учетом найденных ранее независимых начальных условий:
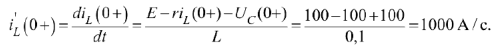
Подставляя начальные условия в уравнения для определения постоянной интегрирования
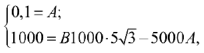
получим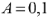 
и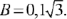 
С учетом найденных постоянных интегрирования переходный процесс по току в индуктивности можно записать в виде
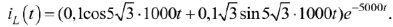
По найденным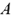 
и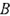 
перейдём к одной гармонической функции с начальной фазой:
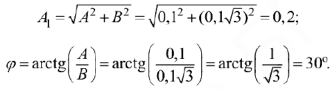
Окончательно имеем
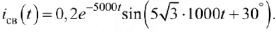
Аналогично рассчитаем переходный процесс по напряжению на емкости:
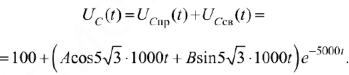
Возьмем производную
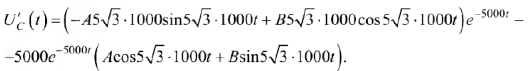
Полагая 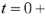в последних уравнениях, получим
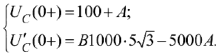
Зависимое начальное условие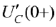 
определим по выражению
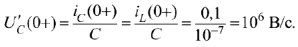
С учетом начальных условий получим систему
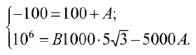
Откуда следует, что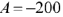 
и 
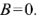
Переходный процесс по напряжению на емкости с учетом 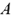и описывается выражением
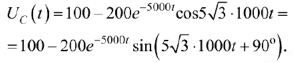
Эта задача взята со страницы решения задач по электротехнике:
Решение задач по электротехнике
Возможно эти задачи вам будут полезны:
| Задача №60 с решением |
| Задача №61 с решением |
| Задача №64 с решением |
| Задача №65 с решением |
