Функция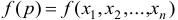 
имеет условный максимум (условный минимум) в т. 
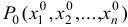, если 
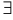такая окрестность точки 
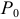, для всех точек 
(
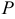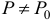), удовлетворяющих уравнениям связи 
.
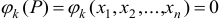Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа:
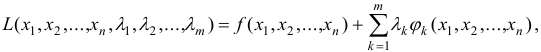
где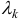 
называются множителями Лагранжа.
В случае функции двух переменных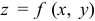 
при уравнении связи 
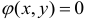функция Лагранжа имеет вид:
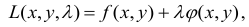
где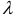 
— неопределенный постоянный множитель Лагранжа.
Необходимые условия экстремума выражаются системой уравнений
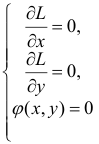или 
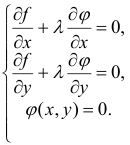
Вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала функции Лагранжа:
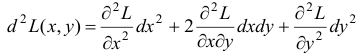
при условии, что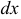 
и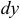 
связаны уравнением:
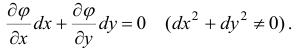
Функция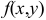 
имеет условный максимум, если 
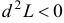, и условный минимум, если 
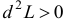. В частности, эти условия эквивалентны достаточным условиям существования экстремума.
Пример:
Найти условный экстремум функции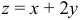 
при условии, что переменные 
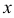и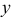 
удовлетворяют уравнению 
.
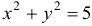Решение:
Составим функцию Лагранжа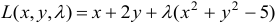 
.
Имеем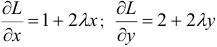 
.
Находим стационарные точки:
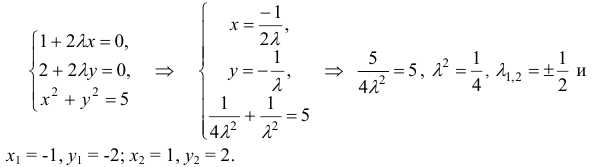
Имеем две стационарные точки 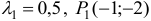для 
и для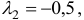 
.
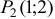Так как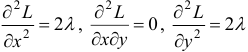 
, то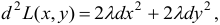 
.
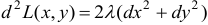Если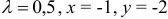 
, то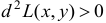 
и данная функция в т.
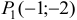имеет условный минимум 
.
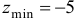Если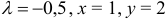 
, то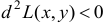 
и данная функция в т. 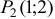имеет условный максимум 
.
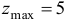Ответ: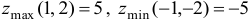 
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Касательная плоскость и нормаль к поверхности |
| Экстремум функции нескольких переменных |
| Производная в данном направлении. Градиент функции |
| Наибольшее и наименьшее значение функции z=f(x,y) |
