Оглавление:
Условный экстремум фнп
В ряде задач на поиск наибольших и наименьших значений ФНП переменные бывают связаны друг с другом некоторыми добавочными условиями. В этом случае говорят об условном экстремуме. Заметим, что необходимым условием разрешимости является то, что число уравнений обязательно меньше числа переменных.
Рассмотрим вопрос об условном экстремуме функции двух переменных, если переменные связаны одним условием.
Пусть требуется найти экстремумы функции
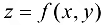
при условии, что 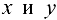 связаны уравнением
связаны уравнением
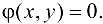
В определенных случаях данная задача может быть решена методом подстановки. Если удастся, например, разрешить уравнение (23.2) относительно 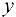 , то, подставляя в (23.1) вместо
, то, подставляя в (23.1) вместо 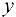 найденное выражение, получим функцию одной переменной
найденное выражение, получим функцию одной переменной 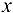 и тогда исходная задача будет сведена к задаче исследования на экстремум функции одной независимой переменной
и тогда исходная задача будет сведена к задаче исследования на экстремум функции одной независимой переменной 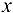 .
.
В случае, когда разрешить уравнение (23.2) не представляется возможным, используют другие методы. В частности, используется метод множителей Лагранжа.
Суть метода сводится к следующему: на основании исходной функции (23.1) и условия связи (23.2) строится вспомогательная функция Лагранжа
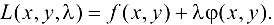
Функция 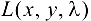 — функция трех переменных.
— функция трех переменных.
Необходимым условием существования экстремума данной функции (в предположении, что исходные функции непрерывно дифференцируемы) является равенство нулю частных производных.
Система для определения критических точек функции Лагранжа имеет вид:
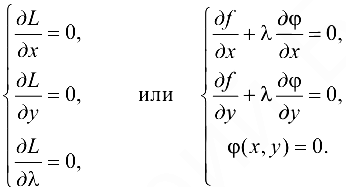
Решения системы (23.3) определяют критические точки функции Лагранжа, а также — критические точки функции (23.1) при условии (23.2).
Достаточные условия условного экстремума связаны с изучением знака дифференциала второго порядка функции Лагранжа.
Теорема 23.1*. Пусть функции 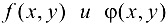 определены и имеют непрерывные частные производные второго порядка в некоторой области D. Пусть точка
определены и имеют непрерывные частные производные второго порядка в некоторой области D. Пусть точка 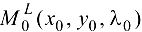 — критическая точка функции
— критическая точка функции 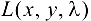 , причем
, причем 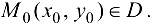 Тогда, если при выполнении условий
Тогда, если при выполнении условий
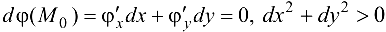
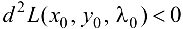 , то в точке
, то в точке 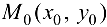 функция
функция 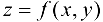 имеет условный максимум;
имеет условный максимум;
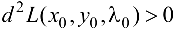 , то в точке
, то в точке 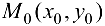 функция
функция 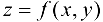 имеет условный минимум.
имеет условный минимум.
Теорема 23.2*. Пусть функции 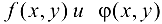 определены и имеют непрерывные частные производные второго порядка в некоторой области D. Пусть точка
определены и имеют непрерывные частные производные второго порядка в некоторой области D. Пусть точка 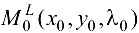 — критическая точка функции
— критическая точка функции 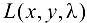 , причем
, причем 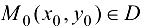 . Тогда если
. Тогда если
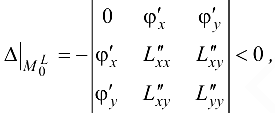
то в точке 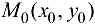 функция
функция 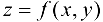 имеет условный максимум; если
имеет условный максимум; если 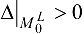 , то в точке
, то в точке 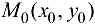 функция
функция 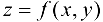 имеет условный минимум.
имеет условный минимум.
Заметим, что параметр 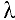 носит вспомогательный характер и в вычислении значений условных экстремумов не используется.
носит вспомогательный характер и в вычислении значений условных экстремумов не используется.
Пример 23.1.
Найти экстремумы функции 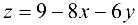 при условии
при условии 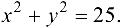
Решение:
Преобразуем условие связи к виду (23.2): 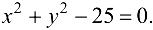
Составим функцию Лагранжа
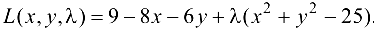
Найдем частные производные функции Лагранжа:
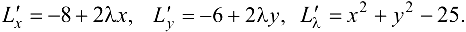
Система для определения критических точек имеет вид:
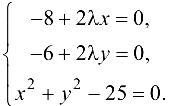
Решив систему, получим: 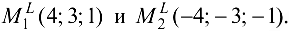 .
.
Для определения характера экстремума найдем частные производные второго порядка функции Лагранжа:
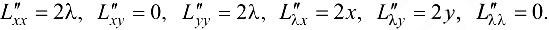
Выполнение условия 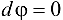 означает:
означает: 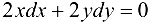 , тогда
, тогда
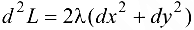
Так как 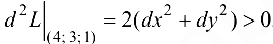 , то в точке
, то в точке 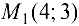 исходная функция имеет условный минимум, причем
исходная функция имеет условный минимум, причем 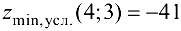 ; так как
; так как 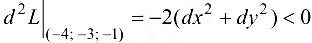 , то в точке
, то в точке 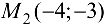 исходная функция имеет условный максимум, причем
исходная функция имеет условный максимум, причем 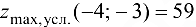 .
.
Для определения характера экстремума с использованием определителя, составим его в общем виде:
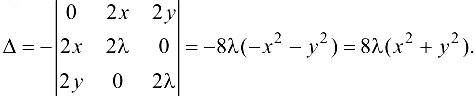
Так как 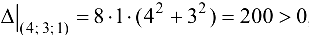 , то в точке
, то в точке 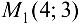 исходная функция имеет условный минимум, причем
исходная функция имеет условный минимум, причем 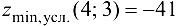 : так как
: так как 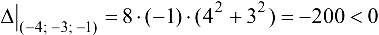 , то в точке
, то в точке 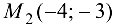 исходная функция имеет условный максимум, причем
исходная функция имеет условный максимум, причем 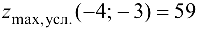 .
.
Ответ: 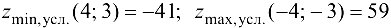 .
.
В случае если требуется найти экстремумы функции n переменных 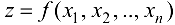 , при условии, что переменные
, при условии, что переменные 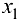 ,
, 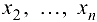 связаны
связаны 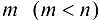 уравнениями связи
уравнениями связи
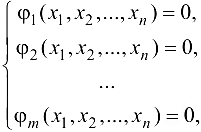
составляется функция Лагранжа с m множителями 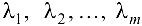 :
:
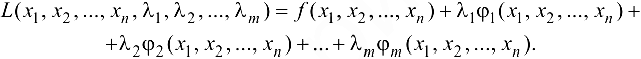
Для определения критических точек необходимо решить систему из 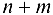 уравнений:
уравнений:
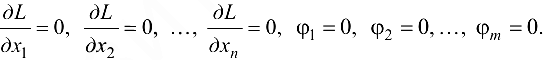
Наличие и характер экстремума можно установить, используя дифференциал второго порядка функции Лагранжа.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

