Условная вероятность с примерами решения и образцами выполнения

Оглавление:

Одним из основных понятий при аксиоматическом построении теории вероятностей является понятие условной вероятности. Именно условная вероятность оценивает то изменение в степени уверенности о наступлении некоторого события, которое происходит после получения дополнительной информации. С помощью условной вероятности определяется независимость событий, формализующая понятие не связанных между собой опытов. Использование условной вероятности в ряде случаев позволяет существенно упростить решение задачи (формулы умножения вероятностей, полной вероятности и Байеса).

Условная вероятность

Рассмотрим два события А и В. Пусть известно, что событие А наступило, но неизвестно, какой конкретно из элементарных исходов 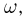Условная вероятность составляющих событие А, произошел. Что можно сказать в этом случае о вероятности наступления события В?

Пример:

Событие А — выпадение четного числа очков на игральной кости, событие В — выпадение нечетного числа очков. Поскольку события А и В несовместны, то при наступлении события А событие В уже не может произойти и ему естественно приписать условную вероятность 0.

Пример:

Событие А — выпадение 4 или 6 очков на игральной кости, событие В — выпадение четного числа очков. Так как событие А принадлежит событию В, то при наступлении события А событие В обязательно произойдет, т.е. событие В имеет условную вероятность 1.

Пример:

Событие А — выпадение четного числа очков на игральной кости, событие В — выпадение не менее 5 очков. Если событие А наступило, то произошел один из трех элементарных исходов: выпало 2, 4 или 6 очков. Но из этих трех исходов только один исход (выпадение «шестерки») влечет за собой появление события В. В соответствии с принципом классической вероятности в данном случае естественно определить условную вероятность события В числом 1/3. Заметим, что в этом примере условная вероятность появления события В совпадает с безусловной.

Из приведенных примеров видно, что условная вероятность может как совпадать с безусловной вероятностью, так и быть меньше или больше нее. Саму же условную вероятность 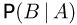события В при условии события А в рамках классической схемы естественно определить как отношение числа исходов Условная вероятность благоприятных для

совместного осуществления событий А и В, к числу исходов 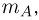Условная вероятность благоприятных для события А т. е.

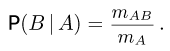
Поделим теперь числитель и знаменатель полученного выражения на общее число n элементарных исходов:

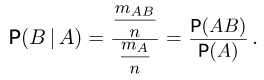
Последняя формула уже может служить общим определением условной вероятности при аксиоматическом подходе. Итак, условной вероятностью события В при условии события 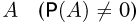Условная вероятность называется отношение вероятности пересечения событий А и В к вероятности события А:

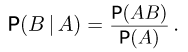
Нетрудно видеть, что условная вероятность обладает всеми свойствами безусловной вероятности. Так,

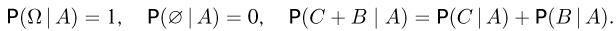
Иногда бывает полезным равенство

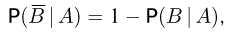
вытекающее из соотношения

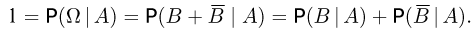
Пример:

При переписи населения Англии и Уэльса в 1891 г. оказалось, что темноволосые отцы и темноволосые сыновья составляют 5% обследованных, темноволосые отцы и светловолосые сыновья — 7,9%, светловолосые отцы и темноволосые сыновья — 8,9%, светловолосые отцы и светловолосые сыновья — 78,2%. Найдем условные вероятности рождения светловолосого сына у темноволосого и светловолосого отцов. Пусть событие А означает, что в случайно выбранной паре отец-сын светловолосым является отец, событие В — светловолосый сын. Тогда событие 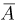Условная вероятность — темноволосый отец, событие 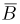— темноволосый сын и из результатов переписи следует, что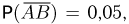

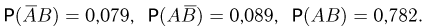
Поэтому

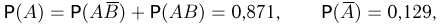
и условная вероятность у темноволосого отца родиться светловолосому сыну

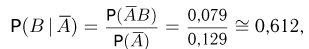
а у светловолосого

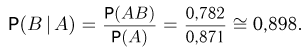
Пример:

При трехкратном подбрасывании симметричной монеты выпало два «герба» (событие А). Определим условную вероятность того, что при втором подбрасывании выпал «герб» (событие В). В этом случае событие АВ состоит в выпадении двух «гербов», один из которых выпал при втором подбрасывании, т. е. содержит 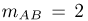Условная вероятность элементарных исходов: «герб»-«герб»-«цифра» и «цифра»-вгерб»-«герб». Поскольку всего у нас 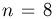элементарных исходов и мы находимся в рамках классической схемы, то 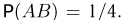Условная вероятность Аналогично, событию А благоприятствуют 3 исхода, и 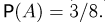Итак, искомая вероятность

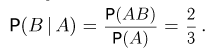
Пример:

Электрон может быть с вероятностью 0,6 обнаружен на одной из четырех орбит атома, причем с равной вероятностью — на любой из них, и с дополнительной вероятностью 0,4 не обнаружен вообще. На первых трех орбитах электрон не обнаружен (событие /1). Найдем вероятность обнаружить его на четвертой орбите (событие В) при этом условии. Поскольку вероятность обнаружить электрон на каждой орбите равна 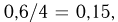Условная вероятность то вероятность не обнаружить электрон на первых трех орбитах 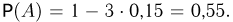Событие АВ — электрон не обнаружен на первых трех орбитах и обнаружен на четвертой орбите — совпадает просто с событием В — электрон находится на четвертой орбите и имеет вероятность 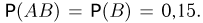Условная вероятность Искомая вероятность, равная условной вероятности события В при условии события А, в этом случае имеет вид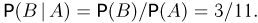

Условные вероятности

Конечное вероятностное пространство. Классическое определение вероятности	Формула полной вероятности
Геометрические вероятности	Формула Байеса

Решение заданий и задач по предметам:

Дополнительные лекции по теории вероятностей: