Условие непрерывности монотонной функции

Условие непрерывности монотонной функции

Условие непрерывности монотонной функции. Рассматриваете ли вы функцию/(X \монотонно возрастающую (убывающую)) в разделе 3? [Н°47]. Тогда какие функции этого типа разнесены на 3?Он устанавливает простую функцию, используя ли вся непрерывность может быть обнаружена немедленно. Теорема интервал 3?Если набор значений монотонной возрастающей (убывающей) функции f (x) входит в определенный интервал и полностью заполнен, то является ли функция f (x) на интервале 3?Непрерывный.

Этот промежуток может быть конечным или бесконечным, замкнутым, полуоткрытым или открытым. Людмила Фирмаль

• )* Из 3 точек взять точки х0?И если предположить, что это не правый край этого интервала, то это доказывает непрерывность функции/(x) в правой точке xj. Аналогично, непрерывность функции в левой точке x $может быть доказана, если Xc не является левым краем рассматриваемого интервала, и это вместе приводит к выводу теоремы.

• Точка y0 = f (x0) принадлежит интервалу 3^, а не самому правому (в конце концов, в 3?). Существует значение x ^> Xa, которое соответствует значению y = f (x)^> y0). пусть e-любое малое положительное число. Впрочем, предположим, что дальше. * ) Предположим, что этот конец является конечным числом. * ( * ) Чтобы быть ясным, предположим, что функция монотонно увеличивается в строгом смысле (но теорема также верна для широкой монотонной функции).

Далее (70) здесь указывает, что условие, сформулированное как достаточное для непрерывности монотонной функции, также необходимо. Людмила Фирмаль

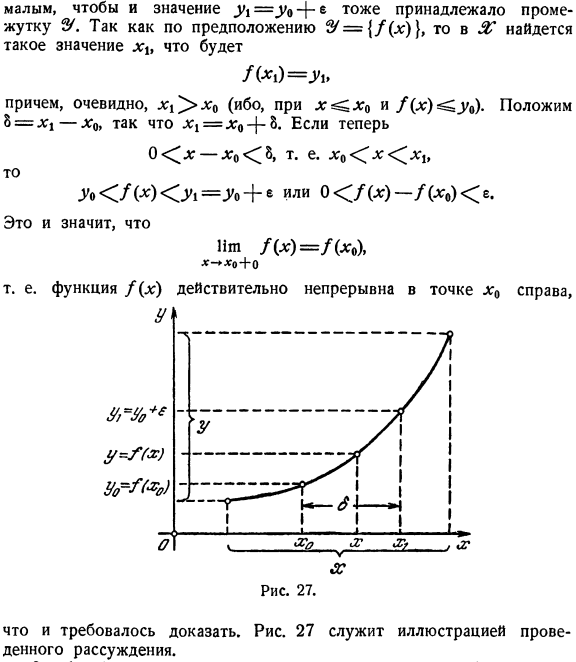
• Поскольку значение yj = y9 {y также настолько мало, что оно принадлежит интервалу ZL, из предположения= \ / (x)},^имеет такое значение: /(Х1)= Йи И, по-видимому, x1 ′> x0 (для u /(x)<yy).Поставь Б-х 1-ХС 0 < ^ q; 0 <8, то есть Л< / М01=Л+ 8 или о</（■）-/（• «）<«• Иначе говоря、 11м /(х)= /(х»）、 х * хо + 0 Если вам нужно доказать.27-это иллюстрация дискуссии.

Смотрите также:

Решение задач по математическому анализу

Непрерывность на конце промежутка сходимости.	Арифметические операции над непрерывными функциями.
Определение непрерывности функции в точке.	Непрерывность элементарных функций.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.