Ускорение точки в сложном движении

Ускорение точки в сложном движении

Теорема Кориолиса:

Между ускорениями точки в подвижной и неподвижной системах отсчета существует более сложная
зависимость, чем между скоростями. Эта зависимость впервые
была установлена французским механиком Г. Кориолисом A792—1843) при аналитическом изучении движения материальной точки.
Чтобы выяснить эту зависимость, рассмотрим движение материальной точки М в подвижной системе 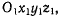которая в свою
очередь совершает некоторое движение относительно неподвижной
системы отсчета Oxyz (например, материальная точка перемещается
по твердому телу, которое само движется относительно
неподвижной системы координат).

Теорема Кориолиса:

Абсолютное ускорение материальной точки равно геометрической сумме ускорений: относительного,
переносного и добавочного.

Доказательство. Обозначим через х, у, z координаты точки М относительно неподвижной системы отсчета, через
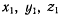— ее координаты относительно подвижной системы отсчета. Формулы преобразования устанавливают зависимость между
координатами точки в подвижной и неподвижной системах:

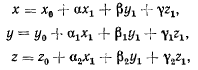
где 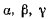— направляющие косинусы углов между осями подвижной и неподвижной систем координат, заданные таблицей

Формулы преобразования (а) справедливы для любого момента
времени. Дифференцируя их по времени, получим

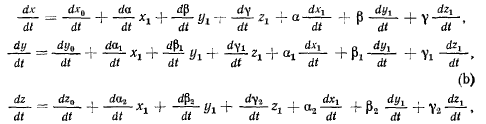
где выражение

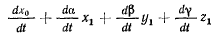
представляет собой проекцию переносной скорости точки на ось х,
а выражение 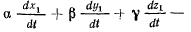проекцию относительной
скорости точки на ось х. Аналогичные соотношения получаем и для других осей.

Дифференцируя еще раз равенства (b), получим

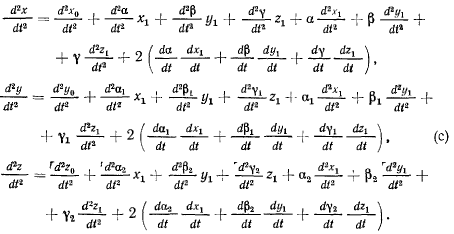
Переносным ускорением точки назовем ускорение
той точки подвижной системы координат, которая совпадает в
данный момент с движущейся материальной точкой М. Проекции
переносного ускорения 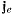на неподвижные оси координат найдем,
положив в формулах (с) координаты 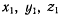постоянными величинами. Тогда для проекций переносного ускорения будем иметь
выражения

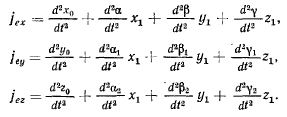
Положение точки в подвижной системе координат определяется ее координатами и вектор относительного ускорения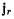
точки будет иметь проекции на оси 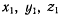равные вторым про-
производным от координат 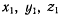по времени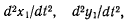 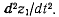Проекции вектора относительного ускорения на неподвижные оси координат получим непосредственно из формул преобразования

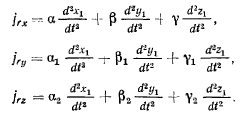
Рассмотрим еще вектор 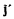с проекциями

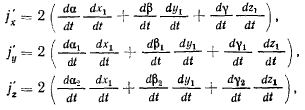
который будем называть вектором добавочного, или
поворотного, ускорения точки (ускорения Кориолиса). Проекции
вектора абсолютного ускорения точки на неподвижные оси
координат можно теперь представить в виде суммы трех членов:

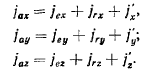
Откуда сразу же получим векторную формулу

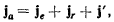
т. е. абсолютное ускорение точки равно геометрической сумме переносного, относительного и добавочного ускорений.
Выясняя механический смысл добавочного ускорения, заметим
следующие его свойства:

1. Добавочное ускорение обращается в нуль, если подвижная
   система координат не вращается, а движется поступательно,
   поскольку в этом случае обращаются в нуль производные от
   направляющих косинусов подвижной системы осей.
2. Добавочное ускорение обращается в нуль, если равна нулю
   скорость относительного движения материальной точки.
   Рассмотрим проекции вектора добавочного ускорения на по-
   подвижные оси координат

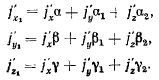
Подставляя сюда значения проекций 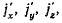получим

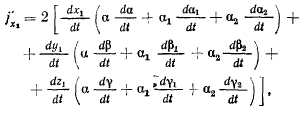
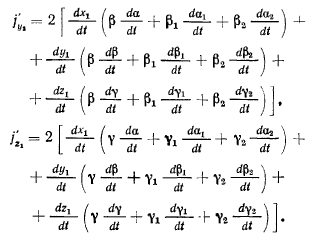
Дифференцируя теперь тождественные соотношения

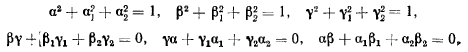
найдем

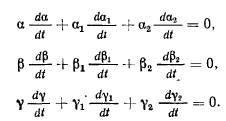
Вводя обозначения

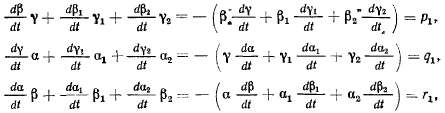
полученные формулы для проекций добавочного ускорения перепишем в виде

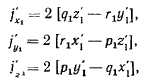
¦что можно представить одной векторной формулой

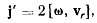
где 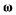— вектор мгновенной угловой скорости вращения подвижной
системы координат, имеющий проекции на подвижные оси координат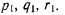
Сопоставляя полученную формулу с формулой Эйлера

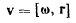
.для определения скоростей точек твердого тела в случае мгновенного вращения последнего, заметим, что вектор добавочного ускорения направлен в сторону вращения (вместе с системой координат) конца вектора относительной скорости точки (рис. 65).

Пример:

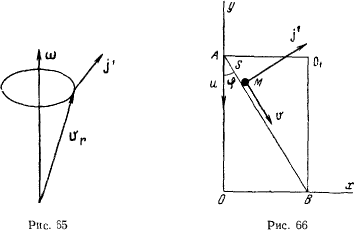
Палочка АВ скользит своими концами по неподвижным
вертикальной и горизонтальной прямым так, что конец А движется с постоянной скоростью 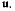По палочке движется точка М с постоянной относительной скоростью v. Определить абсолютные скорость и ускорение точки М (рис. 66).

Решение:

Мгновенный центр вращения палочки находится в точке 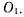с координатами

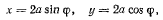
где 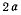— длина палочки, а 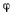— угол между палочкой и вертикальной прямой Обозначая через s расстояние точки М от конца А палочки, для координат точки М получим значения

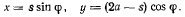
Проекции переносной скорости точки М на неподвижные оси координат получим, рассматривая движение точки М палочки. Эти проекции можно вычислить по формулам Эйлера, рассматривая мгновенное вращение палочки вокруг точки 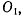Эти же проекции можно найти непосредственным дифференцированием уравнений (а), предполагая постоянной величину s

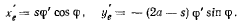
Для определения величины 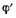рассмотрим скорость точки А:

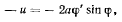
откуда

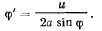
Тогда для проекций переносной скорости на оси х, у будем иметь

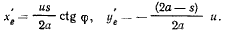
Проекции относительной скорости точки получим, рассматривая движение точки по палочке

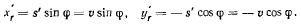
Воспользовавшись теоремой о сложении скоростей, найдем проекции
абсолютной скорости

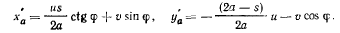
Ускорение точки определим при помощи теоремы Кориолиса. При этом переносное ускорение получим дифференцированием уравнений (с) в предположении, что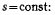

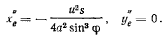
Если точка движется по палочке с постоянной скоростью v, то относительное ускорение равно нулю, а проекции добавочного ускорения точки получим из матрицы

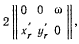
откуда

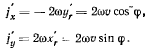
По теореме Кориолиса проекции абсолютного ускорения будут теперь равны

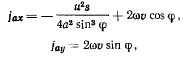
или, после подстановки значения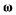

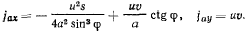
Направления переносного и добавочного ускорений легко определить
геометрически (рис. 67).

Пример:

Палочка вращается в плоскости чертежа вокруг неподвижной точки О, причем угол, который она образует с неподвижной прямой, меняется по произвольно заданному закону 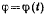Вдоль палочки скользит ползунок по заданному закону 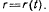Определить ускорение ползунка в зависимости от его положения (рис. 68).

Решение:

Применим теорему Кориолиса. В переносном движении точка движется по окружности, поэтому переносное ускорение
может быть задано касательной и нормальной составляющими

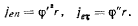
Относительное движение точки прямолинейное, а относительное ускорение точки направлено вдоль палочки

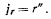
Добавочное ускорение

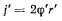
будет направлено ортогонально к палочке в сторону ее вращения, если принимать положительную относительную скорость направленной вдоль палочки от

точки О. Проектируя ускорение на направление палочки и на ортогональное к ней направление, получим радиальную и трансверсальную составляющие ускорения

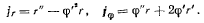
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Мгновенное движение твердого тела с одной неподвижной точкой

Плоскопараллельное движение твердого тела

Замечание о дифференцировании единичного вектора

Векторный вывод теоремы Кориолиса