Оглавление:



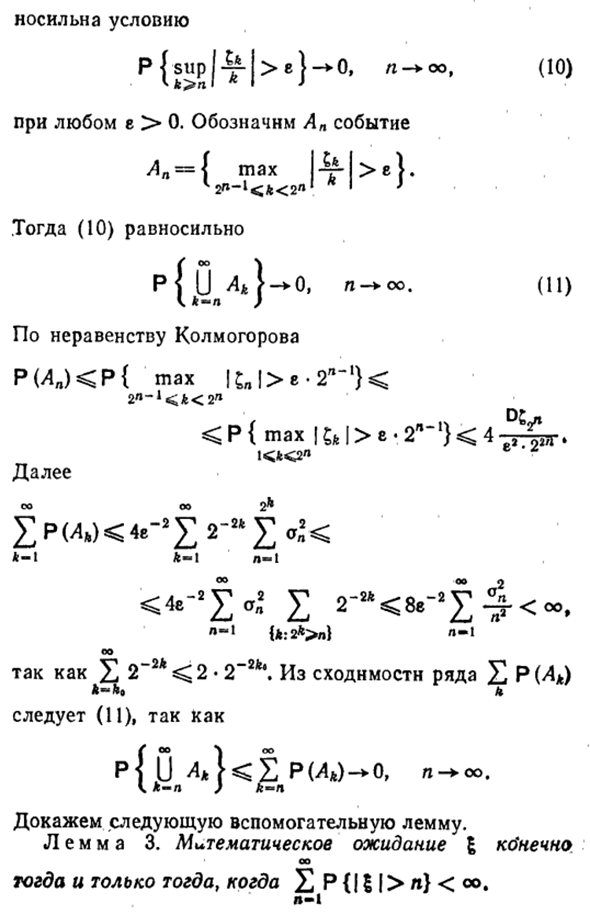




Усиленный закон больших чисел
- Много сильных законов На основе чебышевского неравенства Всего Ха == Ei ‘+! Его можно сформулировать следующим образом: если £ 2 «… является независимым и D £ a ограничено, н х ‘ | Если bh> независимы и равномерно распределены, то сходимость вероятности (7) слабее с конечным условием = Теорема 5 (Кингчин). … если независим.
- Если они равномерно распределены и = i, то, конечно, выполняется много законов. … JL- -l— 1 Доказательство. Поскольку характеристическая функция / (/) — а случайной величины выражается вблизи нуля в виде / (/) = 1 + о (/), C = … + BN-PA> ^ (‘ЧК-ОГ- * 1’ откуда следует слабая сходимость t’Jn к нулю. Эквивалентны (см. Теорему 3 и 4 в § 48) b> ‘n1n- * 0- В условиях теоремы 1 А.
Оказывается, что более сильное утверждение, принадлежащее Н. Колмогорову, может быть доказано. Людмила Фирмаль
Это ряд так называемых усиленных законов, II + III + июля „-l- Далее нам нужно неравенство Колмогорова, которое усиливает известное неравенство Чебышева. Теорема 6. (неравенство Колмогорова) делает 1 и … независимым и имеет конечное Ms * u P {max | £ * -M £ k |> n:} <^. (8) \ Z M £ n / (v — «= -t M (6, + … + + А-1 + 2 I M (g, + … + g *) / (v- * i (S * + i + •• + In), k-1 Случайная переменная зависит только от Таким образом (!, + … + lk) / {v.k} не зависит от … -m (e, + … + g / {v.,} • m (1l + 1 + … + y = 0.
Для oe {v = t} ^ x и P {v xh, поэтому Mtf> Z Md / (v — «> x2P {v (9) N Доказательство. = gj -f ….. Согласно критерию (3) §48 сходимость (9) условно p {sup | £ |> e} — * 0, (10) Если е> 0. An = {check> e} указывает на событие An. (10) эквивалентно p {jbi} -0. Сока (Ии) По неравенству Колмогорова P (LP) * -T ~ 1) < e.2n-1} <4-rW> К следующему К- \ А-1 П — Я о U: 2 *> нДж пш \ о От £ 2 до 2 * <2 • 2 до ** \ к \ от сходимости ряда Р ((Λ) 4 фута (11) или позже ^ oo \ oo P (LL) -0, n- * oo.
- Докажем следующую вспомогательную лемму. Лемма 3. Магические ожидания Тика о Только если РP {111> n} <00 н-1 Доказательство. Если Ms конечно, Af Af | £ i конечно и наоборот. Из очевидного неравенства Z (A-1) P {n-I <| 61 «} <1 + 1 P {|| 1> P). l-0 l-1 о E (c-1) P {n-1 o} = E p {| g |> n} P- * 1 л — 1 неравенство Ой ой ой ой £ P {C1> P} Pb L-1 L-1 Отсюда вытекает утверждение леммы. Для независимых и равномерно распределенных случайных величин применяется более сильное утверждение.
Это дает необходимые и достаточные условия для ряда усиленных законов. Теорема 8. (Расширенный закон больших чисел Колмогорова.) Пусть | i, £ 2. … независимый и равномерно распределенный. Делать ч + ч + … ± 1п н Необходимо и достаточно, чтобы существовало конечное M 1n = a. Доказательство. Достаточно.
Введите случайную величину ° > n ~ 1o, 1 л для 16 Дж> я, И -11+ … + ln. Людмила Фирмаль
Случайные величины § ,, l2t также независимы. Xia-PD _ G i-U | — | f L / I Q \ th rt 1 7l Если мы покажем, что все три члена с вероятностью 1 сходятся к нулю справа, мы заключаем, что теорема доказана. Третий член не является случайным и бесконечным, поскольку он равен среднему арифметическому н фе-л Сходимость к нулю 0 «к-йо, член. Обозначим = Ф! *} • у нас есть РP (LO-ep (1L.1> n) -EP (1L>)). п-л л-1 л-1
Где последняя последовательность сходится из-за конечности Mh согласно доказанной лемме. Таким образом, по лемме Бореля – Кантери конечное число n В ф в. Следовательно, (12) C-n / an и * -n ^ n — осталось доказать ►0. Примените теорему 3. Для этого и н-1 о DL оо р D £ n__V1 V ** От A-1 L-t до -1 о 1 L-1 n ^ H о -JVP ^ -KU.K *}! ^ — с того времени £, £ — ^ <7+ n> ft ft n> ft и * + \ K2 И «1 фут-я о <£ (A + l) P {ft-l <2 + M | 6, | <«>. Ft-l Г. р.
Необходимость. Если так • n p »d►O, То есть с вероятностью 1 реализовано только конечное число событий> 1. Лемма Бореля-Кантери дает I p {iu> n} — £ p {i6, i> ii} <oo. п-1 п-1 Таким образом, в лемме этого параграфа результат конечен. О плане успеха Бернулли Мало того, что многие законы имеют место, — Но много сильных законов также Илья 1 Следы Это следует теореме 8. = = li + … где 1 и … независимы и P {| * = » N £ n _ tn _ n ~ \ 9 Sn-t P ft P / 1—1
Смотрите также:
Решение задач по математической статистике
Если вам потребуется заказать решение математической статистики вы всегда можете написать мне в whatsapp.

