Уравнение Бернулли для установившегося потока вязкой жидкости

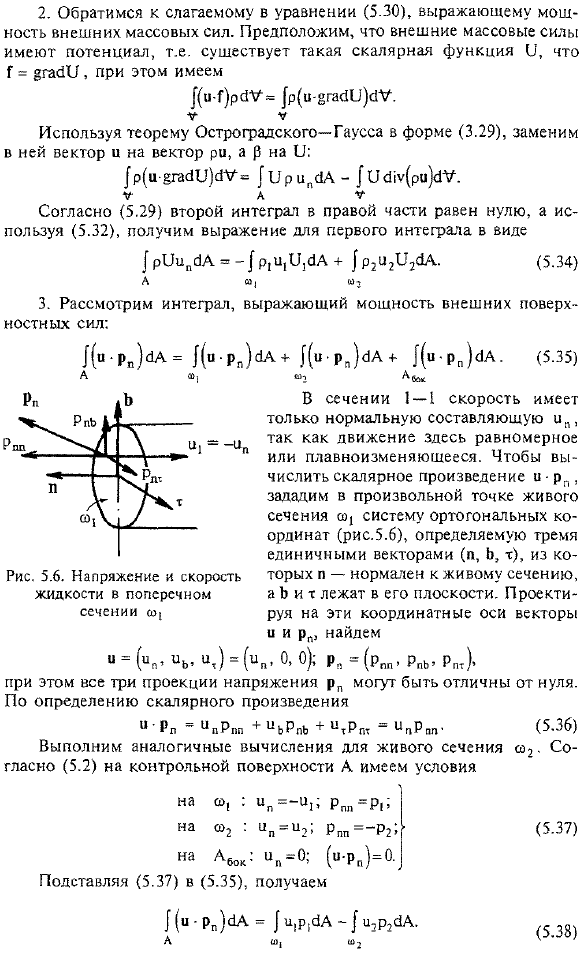
Уравнение Бернулли для установившегося потока вязкой жидкости

Уравнение Бернулли для установившегося потока вязкой жидкости. Выберите в трубопроводе(рис. 5.5}секции 1-1 и 2-2, если движение равномерное или плавно меняется, то управление Объем V, ограниченный плоскостью отсчета A. это обозначается пунктирной линией. Опишите законы изменения кинетической энергии для заданного объема V. Преобразуем члены этого уравнения, выражаем объемный Интеграл в виде поверхности и описываем его как сумму A, как в разделе 5.4, используя условия управляемой поверхности A. 1.

Уравнение Бернулли представляет собой представление закона изменения кинематической энергии, примененного к задаче гидродинамики. Людмила Фирмаль

• Представляет собой существенную производную в виде Движение жидкости стабильно, поэтому первый член равен нулю. Состояние пилотного крыла а имеет вид, показанный на рисунке 5.5） Используйте (5.32), (5.11) и (5.21) для преобразования 2-го члена в (5.31). 2.Перейдем к разделу формулы (5.30), который выражает силу внешней массовой силы. Предположим, что существует потенциал для внешних массовых сил. Существует скалярная функция, такая как Γ= & gas; далее、 |(И. Г)СШ№= | п (я-<sup class=»reg»>®</sup>gasth) с с с. Используя форму теоремы острограда-Гаусса (3.29), заменим вектор η в ней вектором ri и p на 13. Согласно (5.29), 2-й Интеграл справа равен нулю, а используя (5.32), получим выражение первого интеграла в виде: 3.

• Рассмотрим Интеграл, представляющий силу внешней поверхностной силы： В сечении 1-1, скорость имеет только нормальную составляющую ООН. Это связано с равномерным или постоянным изменением движения here. To вычислить скалярное произведение u-pn, определить декартову систему координат (рис. 5.6), определяемую 3 единичными векторами (n, b, m) в любой точке биокомпозиции co1.In этот самолет. Если спроецировать векторные и PN для этих осей、 В этом случае все 3 проекции напряжения p0 могут быть non-zero. By определение скалярного произведения Если вы замените (5.37) на (5.35)、 Выполните тот же расчет для живого участка w2.

Согласно (5.2), маневрирующая поверхность крыла а имеет следующие условия: В разделах 1-1 и 2-2 давление этих разделов распределяется по закону гидростатического давления, так как оно учитывает, что движения изменяются равномерно или плавно, согласно (5.3). Добавим равенство(5.34) и(5.38), чтобы найти выражение силы внешней силы, которая может быть преобразована относительно (5.3).Что 11™ §г： 4.Последний абзац (5.30), в котором описывается сила внутренних сил в управляющем объеме, не изменяется.

Также предполагается, что гравитация является единственной внешней массовой силой. Людмила Фирмаль

• Подставляя (5.33) и (5.39) в исходное уравнение (5.30) и разделяя все члены на массовый расход Ov = & ом, получаем искомое уравнение Бернулли. Где этот термин Масса в контролируемом объеме представляет собой силу внутренних сил, связанных с расходом (диссипацией механической энергии в единицу времени). В наиболее важном случае несжимаемой жидкости(p} p2 = p = cp $ 1) уравнение (5.40) принимает вид.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Гидравлические характеристики поперечного сечения потока.
2. Уравнение неразрывности.
3. Уравнение Бернулли для неустановившегося напорного движения вязкой несжимаемой жидкости.
4. Уравнение Бернулли для установившегося безнапорного движения вязкой жидкости.