Упрощения и анализ уравнений мелкой воды

Упрощения и анализ уравнений мелкой воды

Упрощения и анализ уравнений мелкой воды. Во-первых, мы исключаем так называемый конвективный член ЕС е y-и y-очень мало по сравнению с » э-э Остальные условия. Затем мы линеаризуем их equations. In при нестационарном движении мы предполагаем, что отклонение свободной поверхности от горизонтальной плоскости, независимое от удельного времени, соответствующего глубине L0, значительно меньше глубины L0 или L (рис. 10.2).То есть, если глубина b (x, 1) равна Возмущение свободной поверхности^(x, 1) значительно меньше глубины движения b0 без равномерного perturbation. So в результате мы представляем систему уравнений(10L4) в линеаризованном виде. Полученная система (YL8) аналогична системе уравнений водораздела (7L 9).Поэтому, чтобы проанализировать эту систему, сек.

Вводя новую искомую функцию, система векторных волновых уравнений преобразуется в скалярную систему уравнений. Людмила Фирмаль

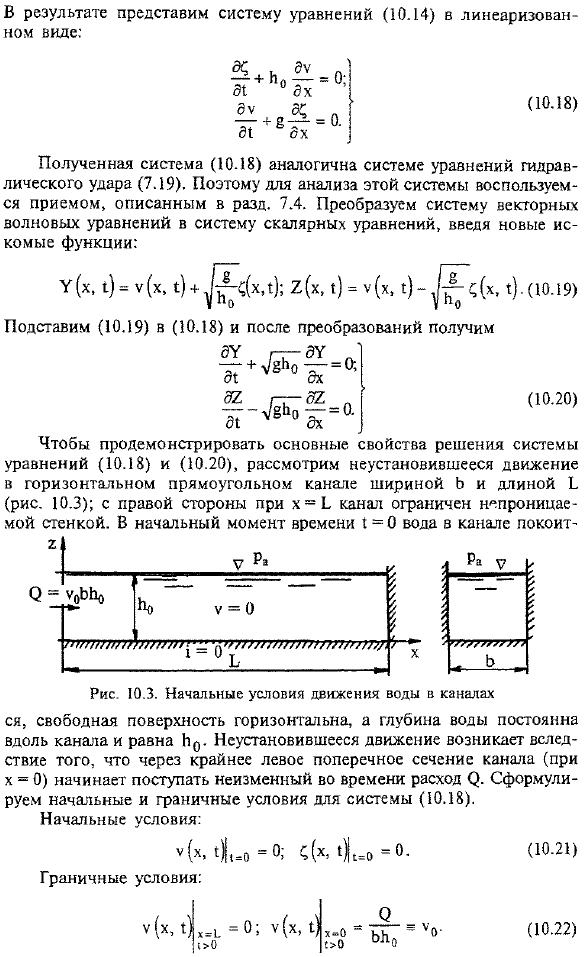
• Чтобы показать основные свойства решения уравнений(10.18) и (10.20), рассмотрим нестационарное движение в горизонтальных прямоугольных каналах шириной B и длиной B(рис. 10.3). на правой стороне x = b канал окружен стенами, которые не могут penetrate. At в первый момент времени 1 = 0, вода в канале остается неподвижной Свободная поверхность горизонтальна, глубина воды постоянна вдоль канала, равна H0.Сформулируем начальные и граничные условия системы (10.18). Стартовые условия： Граничное условие： Разделите длину канала b на 2 равные части Dx-b / 2.Форма уравнения характеристической линии системы (10.18) имеет вид D1 = Ak / ^ $ b. используйте временной шаг, равный 0.В соответствии с уравнением (10.20) функции Y и 2 являются постоянными вдоль характерных линий (10.23) и (10.24) соответственно.

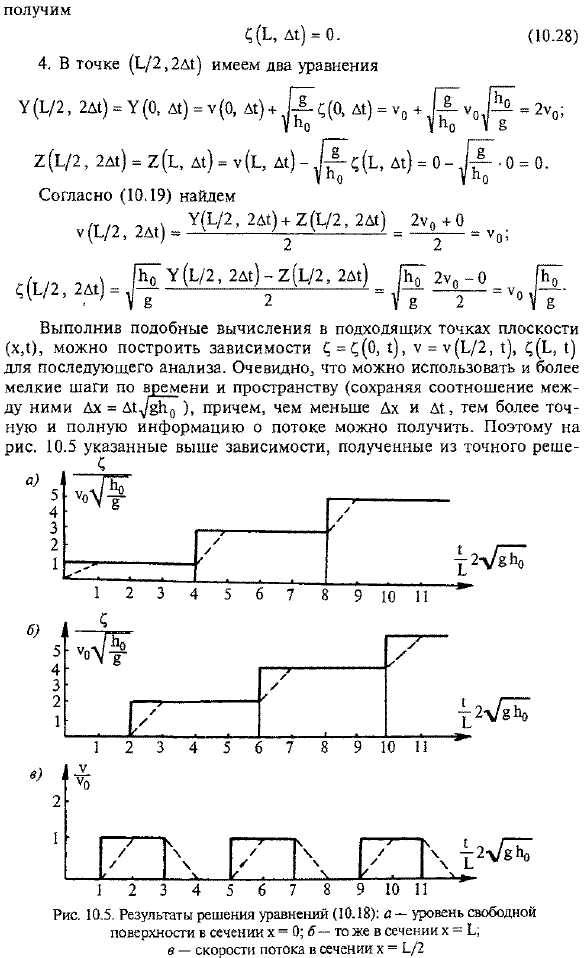
Исходя из этого, мы покажем, как вычислить физические величины (изменения скорости воды V и глубины C) в любой точке плоскости (x, d) На рисунке 5. 10.4. 1.Очки (0, A!), Значение 2 равно значению той же функции в точке (b / 2, 0).Потому что обе эти точки находятся на одной характерной линии. Подставляя уравнение (2) в терминах физических величин (10.25), в соответствии с используемыми начальными и граничными условиями. 2.Точек (0, 2×1) и в предыдущей точке、 3.At в точке (b, q) можно использовать инвариантность функции Y вдоль характеристической линии x = r + b / 2.Используйте начальные и граничные условия. Мы получаем 4.Точка (b / 2.2 DE) имеет 2 уравнения, и, выполнив аналогичный расчет в соответствующей точке плоскости (x, E), зависимость C = C(0>*) «y-Y(b / 2, I), 1) для последующего анализа.

• Очевидно, что можно использовать меньшие шаги во времени и пространстве(сохраняя соотношение Dx = DE ^ / VC), и кроме того, чем меньше Dx и DE вы получите, тем точнее и полнее будет информация о потоке. Следовательно, приведенная выше зависимость, полученная из рисунка 10.5, является точным решением Диаграмма S. 5.Результат решения уравнения (10.18): а-уровень свободной поверхности сечения x = 0. 6-сечение x = C в этом же является расходом сечения x = 1 / 2. Среди следующих анализов следует отметить, что при неустойчивом движении открытого водного пути объем играет ту же роль Уравнения системы минут Dx и Dt(10.18) обозначены сплошной линией, а результаты, полученные с помощью принятых Dx, L / 2 и D1 = L, обозначены пунктирной линией.

Для При описании гидроудара (нестационарного движения напорного трубопровода) скорость волны(скорость распространения возмущений вдоль потока) воспроизводится в величине а (см. Главу 7).Это означает, что скорость перемещения вдоль потока в открытом канале малого возмущения, полученная из обоих уравнений характеристических линий (10.19) и (10.23), (10.24) и (7.31), свободна. С =(10.29） Это хорошо известное уравнение Лагранжа для скорости малоамплитудных гравитационных волн на мелководье (скорость жидкости 0 в открытом канале на конечной глубине L0). для определения скорости волны в относительно стационарной (связанной со дном канала) системе координат в точке ненулевой скорости V ^ 0 воды необходимо наложить скорость c на скорость V.

Нестационарное движение происходит потому, что постоянный расход 3 начинает вытекать из крайнего левого сечения канала (x = 0). Людмила Фирмаль

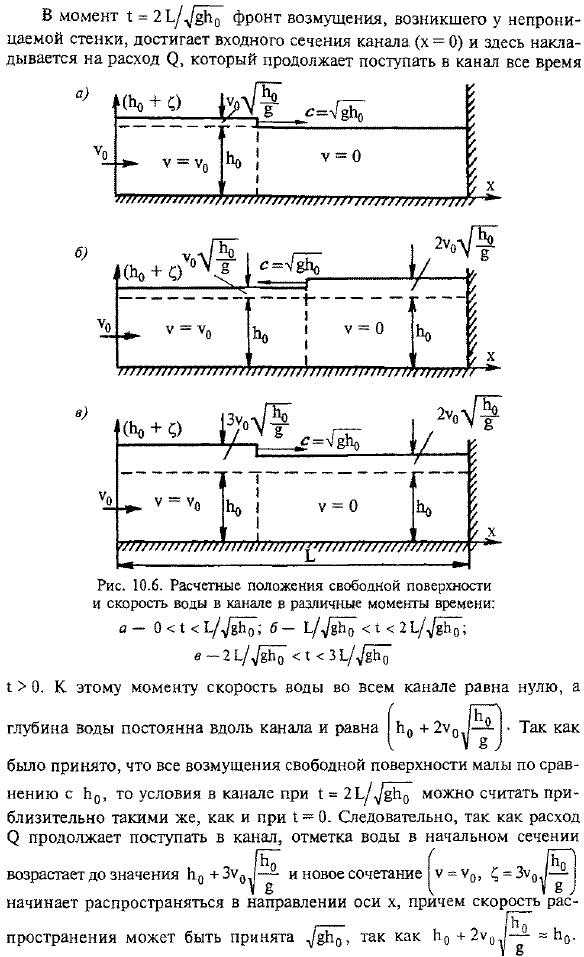
• In кроме того, в отличие от скорости распространения возмущения в трубопроводе, скорость A течет V, величина которой обычно имеет тот же порядок, что и скорость воды Крытые каналы. Вы можете объяснить явления, происходящие в канале с результатами расчета 10.5 и 1> 0, показанными выше. В тот момент, когда расход 0 начинает поступать в канал из входного сечения x = 0, а скорость воды в этом сечении равна Y0-3/10, отметка свободной поверхности этого же сечения немедленно увеличивается Скорость c = м] в направлении оси х, раненых и пострадавших в результате ввода Распространиться Г-н поперечное сечение.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Неустановившееся движение жидкости в открытых руслах (модель мелкой воды).
2. Основные уравнения неустановившегося движения в открытых руслах.
3. Классификация длинных волн в каналах.
4. Общее описание гидравлического прыжка.