Задача №105.
Тренога 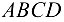 шарнирно опирается на горизонтальную плоскость (рис. 4.13, а) в точках
шарнирно опирается на горизонтальную плоскость (рис. 4.13, а) в точках 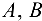 и
и 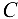 . В точке
. В точке 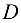 тренога имеет блок. Через блок перекинут гибкий трос, один конец которого закреплен в точке
тренога имеет блок. Через блок перекинут гибкий трос, один конец которого закреплен в точке 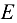 стены, а к другому прикреплен груз
стены, а к другому прикреплен груз 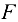 = 10 кН. Определить реакции стержней треноги.
= 10 кН. Определить реакции стержней треноги.
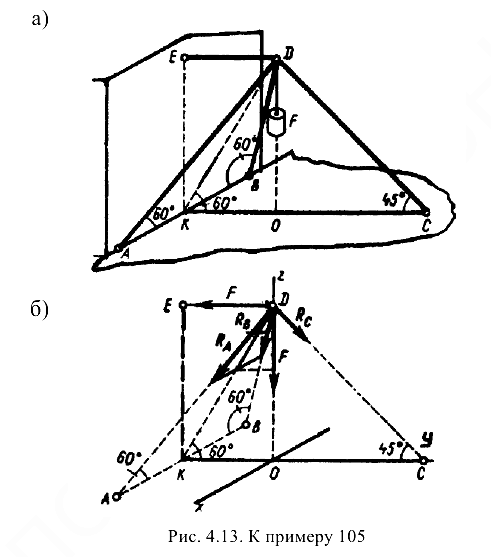
- Пренебрегая размерами блока, считаем, что заданные силы и искомые реакции стержней приложены к точке
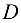 — вершине трехгранной пирамиды, образуемой треногой. На точку
— вершине трехгранной пирамиды, образуемой треногой. На точку 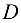 действуют вертикально вниз и горизонтально влево силы натяжения ветвей троса, равные силе тяжести груза
действуют вертикально вниз и горизонтально влево силы натяжения ветвей троса, равные силе тяжести груза 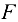 , а также три реакции
, а также три реакции 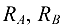 и
и 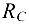 стержней треноги.
стержней треноги. - Систему пяти сил, действующих на точку
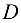 , в выбранных осях координат изобразим на рис. 4.13, б; реакции
, в выбранных осях координат изобразим на рис. 4.13, б; реакции 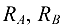 и
и 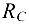 стержней направлены вдоль стержней от точки
стержней направлены вдоль стержней от точки 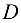 (из предположения, что все стержни растянуты).
(из предположения, что все стержни растянуты). - Прежде чем приступить к составлению уравнений равновесия, следует заметить, что силы, лежащие в плоскости, перпендикулярной какой-либо оси, проецируются на эту ось в виде точки (т. е. проекции равны нулю). Например, обе силы
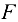 (вертикальная и горизонтальная) и сила
(вертикальная и горизонтальная) и сила 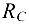 лежат в плоскости, перпендикулярной оси
лежат в плоскости, перпендикулярной оси 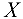 . Поэтому на ось
. Поэтому на ось 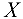 проецируются лишь силы
проецируются лишь силы 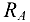 и
и 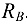 . Рассуждая аналогично, видим, что на ось
. Рассуждая аналогично, видим, что на ось 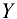 проецируются все силы, кроме вертикальной силы
проецируются все силы, кроме вертикальной силы 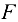 , и на ось
, и на ось 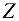 — также все силы, за исключением горизонтальной силы
— также все силы, за исключением горизонтальной силы 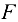 .
.
Составим уравнения равновесия:
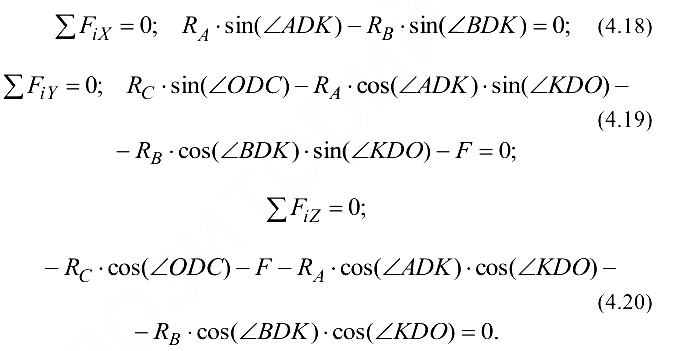
Так как
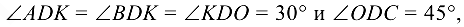
из уравнения (4.18) находим, что 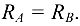
Уравнения (4.19) и (4.20) запишем теперь в виде
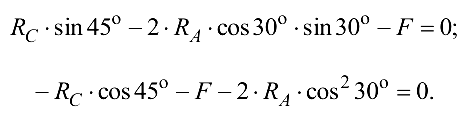
Складывая эти уравнения и учитывая, что
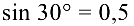
и
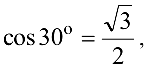
получаем
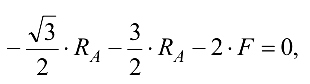
откуда
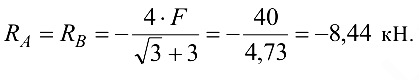
Стержни 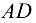 и
и 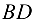 треноги сжаты силой 8,44 кН. Теперь, зная
треноги сжаты силой 8,44 кН. Теперь, зная 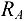 , найдем
, найдем
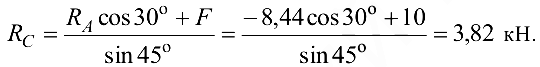
Стержень 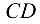 растянут силой 3,82 кН.
растянут силой 3,82 кН.
Ответ:
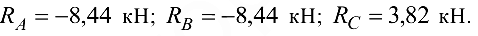
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

