Ток, напряжение, сопротивление и мощность в комплексном виде
Если ток и напряжение изменяются по синусоидальному закону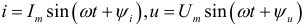 
,то, как указывалось выше их можно изобразить векторами и, следовательно, записать комплексными числами:
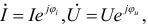
где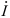 
и 
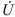— комплексы тока и напряжения. Точка над комплексами указывает, что ток и напряжение изменяются по синусоидальному закону с определенной частото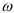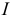й 
; 
и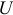 
— модули комплексов тока и напряжения, они же действующие значения тока и напряжения; 
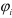и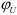 
— аргументы комплексов тока и напряжения, они же начальные фазы тока, 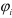и напряжения .
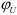Комплекс полного сопротивления цепи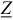 
определяется отношением комплекса напряжения к комплексу тока, т. е.
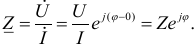
Комплексные величины, не зависящие от времени, обозначаются прописными буквами с черточкой внизу.
Модулем комплекса полного сопротивления является кажущееся сопротивление цепи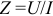 
, а аргументом — угол сдвига фаз между током и напряжением 
.
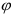Алгебраическая форма записи комплекса полного сопротивления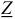 
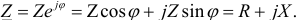
Обратная величина комплекса сопротивления — комплекс проводимости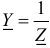 
.
Любую цепь переменного тока можно рассчитывать по законам постоянного тока, если все величины представить в комплексной форме. В этом и заключается достоинство символического метода расчета.
Комплекс полной мощности цепи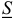 
определяется произведением комплекса напряжения 
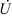и сопряженного комплекса тока 
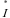(над сопряженным комплексом синусоидальной величины ставят «звёздочку»)
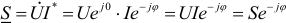
Если комплекс полной мощности 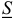перевести из показательной формы в алгебраическую, то получится
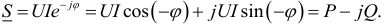
To есть вещественная часть комплекса полной мощности — активная мощность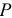 
, а коэффициент при мнимой единице — реактивная мощность 
.
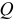Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):
Предмет теоретические основы электротехники
Возможно эти страницы вам будут полезны:
| Проводимость, расчет электрических цепей методом проводимостей |
| Коэффициент мощности |
| Законы Кирхгофа в комплексной форме |
| Трехфазные цепи |
