Перед тем как излагать теорему умножения вероятностей, введем еще одно важное понятие: понятие о независимых и зависимых со- событиях.
Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Рассмотрим примеры. 1) Опыт состоит в бросании двух монет; рассматриваются события:
А — появление герба на первой монете,
В — появление герба на второй монете.
В данном случае вероятность события А не зависит от того, произошло событие В или нет; событие А независимо от со- события В.
2) В урне два белых шара и один черный; два лица вынимают из урны по одному шару; рассматриваются события:
А — появление белого шара у 1-го лица,
В — появление белого шара у 2-го лица.
Вероятность события А до того, как известно что-либо о событии В, равна 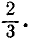 Если стало известно, что событие В произошло, то вероятность события А становится равной
Если стало известно, что событие В произошло, то вероятность события А становится равной 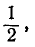 из чего заключаем, что событие А зависит от события В.
из чего заключаем, что событие А зависит от события В.
Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается
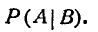
Для условий последнего примера
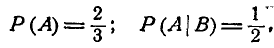
Условие независимости события А от события В можно записать в виде:
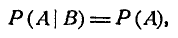
а условие зависимости — в виде:
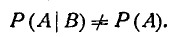
Перейдем к формулировке и доказательству теоремы умножения вероятностей.
Теорема умножения вероятностей формулируется следующим образом.
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
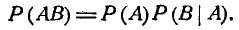 (3.3.1)
(3.3.1)
Пример:
Происходит бой («дуэль») между двумя участниками (летательными аппаратами, танками, кораблями) А и В. У стороны А в запасе два выстрела, у стороны В —одни. Начинает стрельбу А: он делает по В один выстрел и поражает его с вероятностью 0,2. Если В не поражен, он отвечает противнику выстрелом и поражает его с вероятностью 0,3. Если А этим выстрелом не поражен, то он делает по В свой последний выстрел; которым поражает его с вероятностью 0,4. Найти вероятность того, что в бою будет поражен: а) участник А, б) участник В.
Решение:
Рассмотрим события: А — поражение участника А, В — поражение участника В.
Для выполнения события А необходимо совмещение (произведение) двух событий: 1) А не поразил В первым выстрелом и 2) В поразил А своим ответным выстрелом. По теореме умножения вероятностей получим
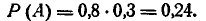
Перейдем к событию В. Оно, очевидно, состоит из двух несовместных вариантов:
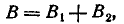
где В1 — поражение участника В первым выстрелом А, В2 — поражение участника В вторым выстрелом А.
По теореме сложения вероятностей
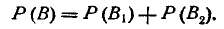
По условию Р (В1) = 0,2. Что касается события В2, то оно представляет собой совмещение (произведение) трех событий, а именно: 1) первый выстрел стороны А не должен поразить В; 2) ответный выстрел стороны В не должен поразить А; 3) последний (второй) выстрел стороны А должен поразить В.
По теореме умножения вероятностей
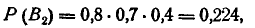
откуда
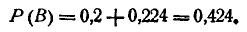
Пример:
Цель, по которой ведется стрельба, состоит из трех различных по уязвимости частей. Для поражения цели достаточно одного попадания в первую часть, или двух попаданий во вторую, или трех попаданий в третью. Если снаряд попал в цель, то вероятность ему попасть в ту или другую часть пропорциональна площади этой части. На проекции цели на плоскость, перпендикулярную направлению стрельбы, первая, вторая и третья части занимают относительные площади 0,1, 0,2 и 0,7. Известно, что в цель попало ровно два снаряда. Найти вероятность того, что цель будет поражена.
Решение:
Обозначим А — поражение цели; Р(А\2) — условную вероятность поражения цели при условии, что в нее попало ровно два снаряда. Два снаряда, попавшие в цель, могут поразить ее двумя способами: или хотя бы один из них попадает в первую часть, или же оба снаряда попадут во вторую. Эти варианты несовместны, так как в цель попало всего два снаряда; поэтому можно применить теорему сложения. Вероятность того, что хотя бы один снаряд попадет в первую часть, может быть вычислена через вероятность противоположного события (ни одни из двух снарядов не попадет в первую часть) и равна 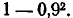 Вероятность того, что оба снаряда попадут во вторую часть, равна
Вероятность того, что оба снаряда попадут во вторую часть, равна 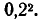 Следовательно,
Следовательно, 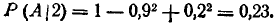
Пример:
Для условий предыдущего примера найти вероятность поражения цели, если известно, что в псе попало три заряда. Решение. Решим задачу двумя способами: через прямое и противоположное событие.
Прямое событие — поражение цели при трех попаданиях — распадается на четыре несовместных варианта:
А1 — хотя бы одно попадание в первую часть, А2 — два попадания во вторую часть и одно — в третью, А3 — три попадания во вторую часть, А4 — три попадания в третью часть.
Вероятность первого варианта находим аналогично предыдущему примеру:
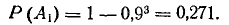
Найдем вероятность второго варианта. Три попавших снаряда могут распределиться по второй н третьей частям нужным образом (два во вторую и один — в третью) тремя способами 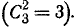 Следовательно,
Следовательно,
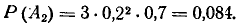
Далее находим:
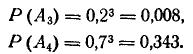
Отсюда
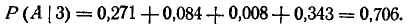
Однако проще решается задача, если перейти к противоположному событию— непоражению цели при трех попаданиях. Это событие может осуществиться только одним способом: если два снаряда из трех попадут в третью часть, а один — во вторую. Таких комбинаций может быть три 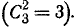 следовательно,
следовательно, 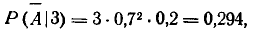
откуда
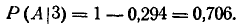
Пример:
Монета бросается 6 раз. Найти вероятность того, что выпадет больше гербов, чем цифр. Решение. Для нахождения вероятности интересующего нас события А (выпадет больше гербов, чем цифр) можно было бы перечислить все возможные его варианты, например:
А1 — выпадет шесть гербов и ни одной цифры, А2 — выпадет пять гербов н одна цифра и т.д.
Однако проще будет применить другой прием. Перечислим все возможные исходы опыта:
А — выпадет больше гербов, чем цифр, В— выпадет больше цифр, чем гербов, С — выпадет одинаковое число цифр и гербов.
События А, В, С несовместны и образуют полную группу. Следовательно,
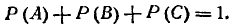
Так как задача симметрична относительно «герба» н «цифры», Р(А)=Р(В),
откуда
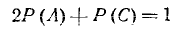
и
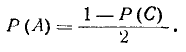
Найдем вероятность события С, состоящего в том, что при шести бросаниях монеты появится ровно три герба (а значит, ровно три цифры). Вероятность любого из вариантов события С (например, последовательности г, ц, г, г, ц, ц при шести бросаниях) одна и та же и равна 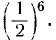 Число таких комбинаций равно
Число таких комбинаций равно 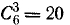 (числу способов, какими можно из шести бросаний выбрать три, в которых появился герб). Следовательно,
(числу способов, какими можно из шести бросаний выбрать три, в которых появился герб). Следовательно,
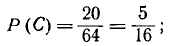
отсюда
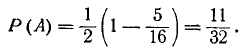
Пример:
Прибор состоит из четырех узлов: А1 А2, А3, А4, причем узел А2 дублирует А1, а узел A4 дублирует узел А3. При отказе (выходе из строя) любого из основных узлов (A1 или А3) происходит автоматической переключение на дублирующий узел. Надежность (вероятность безотказной работы) в течение заданного времени каждого из узлов равна соответственно Р1, Р2, Р3 ,Р4. Надежность каждого из переключающих устройств равна р. Все элементы выходят из строя независимо друг от друга. Определить надежность прибора.
Решение:
Рассмотрим совокупность узлов А1, А2 и соответствующего переключающего устройства как один «обобщенный узел» В, а совокупность узлов А3, A4 и соответствующего переключающего устройства — как обобщенный узел С. Рассмотрим события:
А — безотказная работа прибора, В — безотказная работа обобщенного узла В, С — безотказная работа обобщенного узла С.
Очевидно, А = ВС, откуда
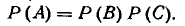
Найдем вероятность события В. Оно распадается на два варианта: А1 — исправно работал узел А1 и 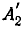 — узел А1 отказал, но оказались исправными переключающее устройство и узел А2. Имеем:
— узел А1 отказал, но оказались исправными переключающее устройство и узел А2. Имеем:

аналогично
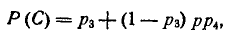
откуда
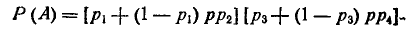
Дополнительные примеры:
Пример:
В лотерее 1000 билетов; из них на один билет падает выигрыш 500 руб., на 10 билетов— выигрыши по 100 руб., на 50 билетов — выигрыши по 20 руб., на 100 билетов — выигрыши но 5 руб., остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выиграть не менее 20 руб.
Решение:
Рассмотрим события:
А —выиграть не менее 20 руб., А1—выиграть 20 руб., А2 — выиграть 100 руб., А3 — выиграть 500 руб.
Очевидно,
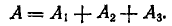
По теореме сложения вероятностей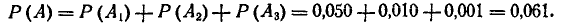
Пример:
Производится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадания в первый склад 0,01; во второй 0,008; в третий 0,025. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны.
Решение:
Рассмотрим события:
А —взрыв складов, А1 — попадание в первый склад, А2 — попадание во второй склад, А3 — попадание в третий склад.
Очевидно,
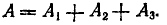
Так как при сбрасывании одной бомбы события А1, А2, А3 несовместны, то
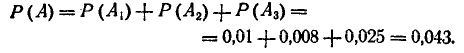
Пример:
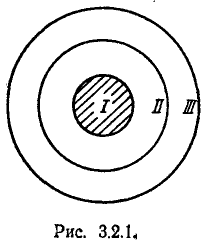
Круговая мишень (рис. 3.2.1) состоит из трех зон: /, II и ///. Вероятность попадания в первую зону при одном выстреле 0,15, во вторую 0,23, в третью 0,17. Найти вероятность промаха.
Решение:
Обозначим А — промах, 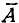 — попадание.
— попадание.
Тогда
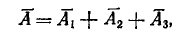
где 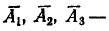 попадание соответственно в первую, вторую и третью зоны
попадание соответственно в первую, вторую и третью зоны
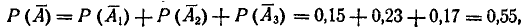
откуда
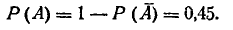
Как уже указывалось, теорема сложения вероятностей (3.2.1) справедлива только для несовместных событий. В случае, когда со- события А и В совместны, вероятность суммы этих событий выражается формулой
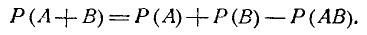 (3.2.3)
(3.2.3)
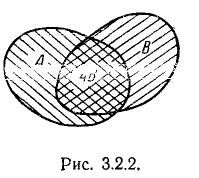
В справедливости формулы (3.2.3) можно наглядно убедиться, рассматривая рис. 3.2.2.
Аналогично вероятность суммы трех совместных событий вычисляется по формуле
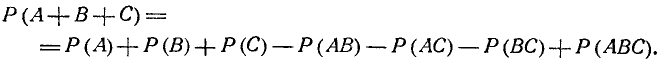
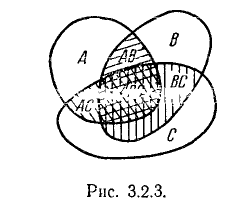
Справедливость этой формулы также наглядно следует из геометрической интерпретации (рис. 3.2.3).
Методом полной индукции можно доказать общую формулу для вероятности суммы любого числа совместных событий, где суммы распространяются на различные значения индексов i; i, j; i, j, k, и т. д.
Формула (3.2.4) выражает вероятность суммы любого числа событий через вероятности произведений этих событий, взятых по одному, по два, по три и т. д.
Аналогичную формулу можно написать для произведения событий. Действительно, из рис. 3.2.2 непосредственно ясно, что 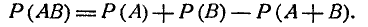 (3.2.5)
(3.2.5)
Из рис. 3.2.3 видно, что 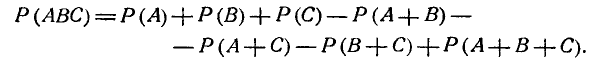 (3.2.6)
(3.2.6)
Общая формула, выражающая вероятность произведения произвольного числа событий через вероятности сумм этих событий, взятых по одному, по два, по три и т. д., имеет вид:
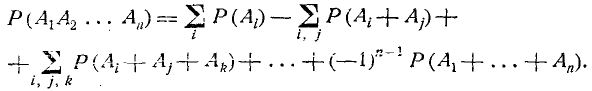 (3.2.7)
(3.2.7)
Формулы типа (3.2.4) и (3.2.7) находят практическое применение при преобразовании различных выражений, содержащих вероятности сумм и произведений событий. В зависимости от специфики задачи в некоторых случаях удобнее бывает пользоваться только суммами, а в других только произведениями событий: для преобразования одних в другие и служат подобные формулы.
Пример:
Техническое устройство состоит из трех агрегатов: двух агрегатов первого типа—-А1 и А2 — и одного агрегата второго типа — В. Агрегаты А1 и А2 дублируют друг друга: при отказе одного из них происходит автоматическое переключение на второй. Агрегат В не дублирован. Для того ‘чтобы устройство прекратило работу (отказало), нужно, чтобы одновременно отказали оба агрегата А1 и А2 или же агрегат В. Таким образом, отказ устройства — событие С — представляется в виде:
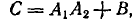
где А1 — отказ агрегата A1, A2 — отказ агрегата А2, В — отказ агрегата В.
Требуется выразить вероятность события С через вероятности событий, содержащих только суммы, а не произведения элементарных событий А1, А2 и В.
Решение:
По формуле (3.2.3) имеем:
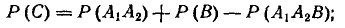 (3.2.8)
(3.2.8)
по формуле (3.2.5)
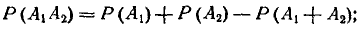
по формуле (3.2.6)
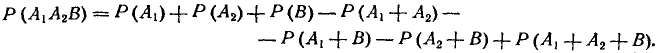
Подставляя эти выражения в (3.2.8) и производя сокращения, получим;
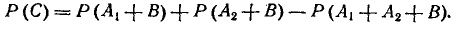
Формула умножения вероятностей
На практике часто происходит так, что известны или достаточно просто определяются именно условные вероятности и с их помощью необходимо вычислить безусловную вероятность некоторого события. Простейшей формулой для решения задач такого типа является формула умножения вероятностей. Пусть имеются события 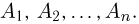 Тогда, используя понятие условной вероятности, можно написать
Тогда, используя понятие условной вероятности, можно написать
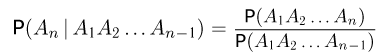
или, умножая на 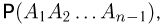
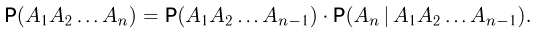
Аналогичным образом
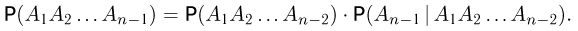
Продолжая эту процедуру, получаем
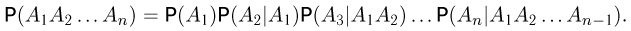
Последнее соотношение носит название формулы умножения вероятностей.
Пример:
На 7 карточках написаны буквы л, л, о, о, о, т, т. Из них последовательно выбираются 4 и кладутся слева направо. Найдем вероятность того, что в результате образуется слово «лото» (событие А). Это — задача на классическую вероятность, и ее можно было бы решить стандартным образом, вычисляя общее число элементарных исходов и число благоприятных для события А исходов. Однако гораздо проще воспользоваться формулой умножения вероятностей. Введем события: 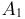 — на первой вынутой карточке написана буква л,
— на первой вынутой карточке написана буква л, 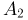 — на второй — буква о,
— на второй — буква о, 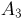 — на третьей — буква
— на третьей — буква 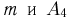 — на четвертой — буква о. Тогда событие А представляет собой пересечение событий
— на четвертой — буква о. Тогда событие А представляет собой пересечение событий 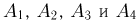 и по формуле умножения вероятностей
и по формуле умножения вероятностей
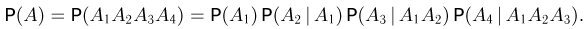
Заметим теперь, что в соответствии с принципом классической вероятности безусловная вероятность 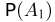 определяется как отношение числа карточек, на которых написана буква л, к общему числу карточек, т.е.
определяется как отношение числа карточек, на которых написана буква л, к общему числу карточек, т.е. 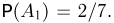 Далее, если событие
Далее, если событие 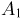 произошло, то у нас осталось 6 карточек и на трех из них написана буква о. Поэтому
произошло, то у нас осталось 6 карточек и на трех из них написана буква о. Поэтому 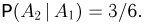 Аналогично, если произошли события
Аналогично, если произошли события 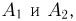 то из пяти оставшихся карточек на двух написана буква т, и, значит,
то из пяти оставшихся карточек на двух написана буква т, и, значит, 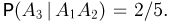 Наконец,
Наконец, 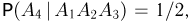 поскольку из четырех оставшихся карточек на двух написана буква о. Окончательно получаем
поскольку из четырех оставшихся карточек на двух написана буква о. Окончательно получаем
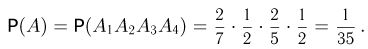
Любознательному читателю предлагаем решить эту задачу с помощью комбинаторных методов.
Пример:
В некоторых сельских местностях России существовало когда-то следующее гадание. Девушка зажимает в руке шесть травинок так, чтобы концы травинок торчали сверху и снизу; подруга связывает эти травинки попарно между собой сверху и снизу в отдельности. Если при этом все шесть травинок оказывались связанными в одно кольцо, то это должно было означать, что девушка в текущем году выйдет замуж. Найдем вероятность того, что травинки при связывании наудачу образуют кольцо (событие A). Для этого предположим сначала, что связаны верхние концы травинок. Тогда у нас образуется 3 пары травинок, и нижние концы этих пар будем последовательно связывать. Пусть событие  означает, что при первом связывании у нас не образуется кольцо (рис. 1), т.е. не будут связаны между собой нижние концы одной и той же пары.
означает, что при первом связывании у нас не образуется кольцо (рис. 1), т.е. не будут связаны между собой нижние концы одной и той же пары.
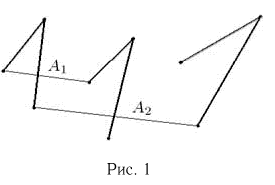
Событие 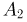 — после второго связывания не образуется кольцо. Тогда событие А представляет собой пересечение событий
— после второго связывания не образуется кольцо. Тогда событие А представляет собой пересечение событий 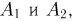 и по формуле умножения вероятностей
и по формуле умножения вероятностей 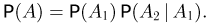 Теперь заметим, что при первом связывании событие
Теперь заметим, что при первом связывании событие 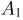 происходит только тогда, когда мы не свяжем между собой концы одной пары, а это возможно в 4 случаях из 5. Поэтому
происходит только тогда, когда мы не свяжем между собой концы одной пары, а это возможно в 4 случаях из 5. Поэтому 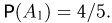 Если событие
Если событие 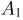 произошло, то для наступления события
произошло, то для наступления события 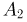 необходимо связать построенную цепь и оставшуюся пару, что в свою очередь можно сделать 2 способами из 3. Значит,
необходимо связать построенную цепь и оставшуюся пару, что в свою очередь можно сделать 2 способами из 3. Значит, 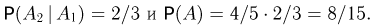
Предоставляем читателю возможность решить эту задачу для 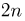 травинок.
травинок.
Следующим важным понятием теории вероятностей является независимость событий. События А и В называются независимыми, если условная вероятность события В при условии А совпадает с безусловной вероятностью события В, т.е. 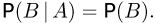
Введенное таким образом понятие скорее можно было бы назвать независимостью события В от события А. Покажем, что на самом деле понятие независимости симметрично относительно перестановки событий А и В, т. е. если событие В не зависит от события А, то событие А также не зависит от события В. Для этого подставим вместо условной вероятности 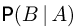 ее значение
ее значение 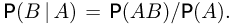 Тогда независимость событий ,4 и JB эквивалентна выполнению равенства
Тогда независимость событий ,4 и JB эквивалентна выполнению равенства
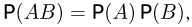
откуда и следует симметричность понятия независимости. Отметим, что последнюю формулу также можно было бы взять в качестве определения независимости. Этим определением можно пользоваться даже в том случае, когда вероятность события А или В равна нулю.
Если события А и В независимы то независимыми являются также пары событий 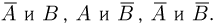 В частности,
В частности,
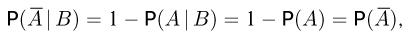
что означает независимость событий 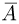 и В. Аналогично доказывается независимость остальных пар событий.
и В. Аналогично доказывается независимость остальных пар событий.
Пример:
Проводится опыт, состоящий из двукратного подбрасывания симметричной монеты. Событие А — выпадение «герба» при первом подбрасывании, событие В — выпадение «герба» при втором. В этом случае, как мы знаем, пространство элементарных исходов 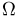 состоит из четырех исходов. Событию А благоприятствуют два исхода, событию В — два исхода и событию АВ — один исход. Значит,
состоит из четырех исходов. Событию А благоприятствуют два исхода, событию В — два исхода и событию АВ — один исход. Значит, 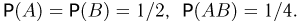 События А и В независимы, поскольку
События А и В независимы, поскольку 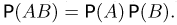
Этот пример подтверждает с точки зрения классической вероятности интуитивный принцип «несвязности» результатов испытаний такого типа, как подбрасывание монеты, бросание игральной кости и т.д. Однако на практике поступают обычно обратным образом. Пусть имеются два различных испытания, причем в первом из них с вероятностью Р(А) может произойти событие А, а во втором с вероятностью Р(В) — событие В. Рассмотрим «обобщенный опыт», результатами которого являются пары 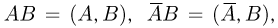
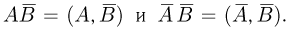 Если априори известно, что результаты испытаний не связаны между собой, то вполне естественно считать события А и В независимыми и положить
Если априори известно, что результаты испытаний не связаны между собой, то вполне естественно считать события А и В независимыми и положить 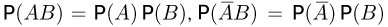 и т.д. В частности, в рассмотренном примере, исходя из двух однократных подбрасываний монеты и независимости результатов подбрасываний, нужно положить для события АВ — выпадение «гербов» при обоих подбрасываниях вероятность
и т.д. В частности, в рассмотренном примере, исходя из двух однократных подбрасываний монеты и независимости результатов подбрасываний, нужно положить для события АВ — выпадение «гербов» при обоих подбрасываниях вероятность 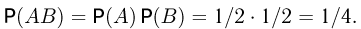
Пример:
Известно, что вероятность двум близнецам быть одного пола примерно равна 0,64, причем вероятность рождения мальчика близка к 0,51. Найдем вероятность того, что второй из близнецов — мальчик (событие В), при условии, что первый из них — также мальчик (событие А). Так как пары мальчик-девочка и девочка-мальчик равновероятны, то вероятность события А — первый ребенок будет мальчиком, а второй — девочкой равна 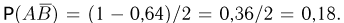 Поскольку из условия задачи
Поскольку из условия задачи 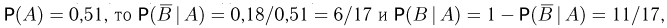 т.е. условная вероятность появления второго мальчика при условии появления первого мальчика существенно больше безусловной вероятности рождения мальчика. Поэтому гипотезу о независимости событий Aw В следует признать ошибочной. С точки зрения генетики это связано с рождением так называемых однояйцевых близнецов.
т.е. условная вероятность появления второго мальчика при условии появления первого мальчика существенно больше безусловной вероятности рождения мальчика. Поэтому гипотезу о независимости событий Aw В следует признать ошибочной. С точки зрения генетики это связано с рождением так называемых однояйцевых близнецов.
Определим теперь понятие независимости событий в совокупности. Назовем события А, В и С независимыми (в совокупности), если 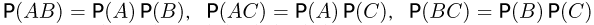 и, кроме того,
и, кроме того, 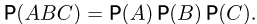 Аналогично определяется понятие независимости в совокупности и большего числа событий: вероятность пересечения любых двух различных событий равна произведению вероятностей этих событий; вероятность пересечения любых трех событий равна произведению их вероятностей;…; вероятность пересечения всех событий равна произведению вероятностей. Из независимости событий в совокупности вытекает их попарная независимость. Однако из попарной независимости, вообще говоря, независимость в совокупности не следует, как показывает следующий простой пример (С. Н. Бернштейн).
Аналогично определяется понятие независимости в совокупности и большего числа событий: вероятность пересечения любых двух различных событий равна произведению вероятностей этих событий; вероятность пересечения любых трех событий равна произведению их вероятностей;…; вероятность пересечения всех событий равна произведению вероятностей. Из независимости событий в совокупности вытекает их попарная независимость. Однако из попарной независимости, вообще говоря, независимость в совокупности не следует, как показывает следующий простой пример (С. Н. Бернштейн).
Пример:
Три грани правильного тетраэдра раскрашены в синий, красный и зеленый цвета, а в раскраске четвертой грани присутствуют все эти цвета. Событие А — тетраэдр упал на грань, в раскраске которой присутствует синий, событие В — красный и событие С — зеленый цвет. Поскольку каждый цвет присутствует в раскраске двух граней из четырех, то 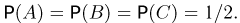 Далее, два цвета присутствуют в раскраске одной грани. Поэтому
Далее, два цвета присутствуют в раскраске одной грани. Поэтому 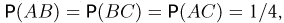 и события А, В ч С попарно независимы. Однако все три цвета присутствуют в раскраске также только одной грани и, значит,
и события А, В ч С попарно независимы. Однако все три цвета присутствуют в раскраске также только одной грани и, значит, 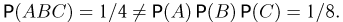 Таким образом, хотя события А, В и С попарно независимы, они зависимы в совокупности.
Таким образом, хотя события А, В и С попарно независимы, они зависимы в совокупности.
Заметим, что когда говорят о независимости событий 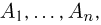 то подразумевают именно независимость событий в совокупности в отличие от попарной независимости событий
то подразумевают именно независимость событий в совокупности в отличие от попарной независимости событий 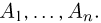
В заключение этого параграфа приведем формулу для вероятности объединения независимых событий. Пусть  Тогда в соответствии с формулой де Моргана
Тогда в соответствии с формулой де Моргана 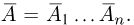 Если события
Если события 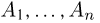 независимы, то события
независимы, то события  также независимы и значит,
также независимы и значит, 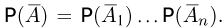 Отсюда окончательно получаем для вероятности объединения независимых событий формулу
Отсюда окончательно получаем для вероятности объединения независимых событий формулу
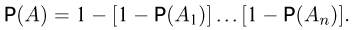
Пример:
Пусть некоторое техническое устройство состоит из п элементов. Назовем соединение этих элементов последовательным (рис. 2), если отказ любого элемента влечет за собой отказ всего устройства. Пусть 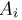
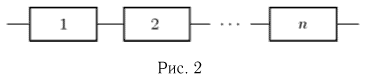
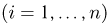 — событие, заключающееся в отказе i-го элемента. Тогда событие А — отказ всего устройства может быть записано в виде
— событие, заключающееся в отказе i-го элемента. Тогда событие А — отказ всего устройства может быть записано в виде 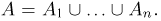 Предполагая, что отказы отдельных элементов независимы, получаем для вероятности отказа всего устройства выражение
Предполагая, что отказы отдельных элементов независимы, получаем для вероятности отказа всего устройства выражение
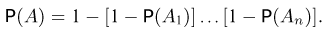
Наряду с последовательным соединением элементов применяется также параллельное соединение (рис. 3), при котором отказ устройства происходит только при отказе всех элементов.
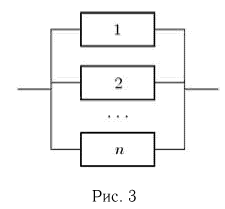
Очевидно, что при параллельном соединении событие А — отказ всего устройства представляет собой пересечение событий 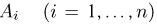 — отказов отдельных элементов, и в случае независимости отказов
— отказов отдельных элементов, и в случае независимости отказов
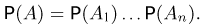
Разумеется, надежность реальных технических устройств определяется более сложными структурными схемами, чем последовательное или параллельное соединение элементов. Однако довольно часто встречаются устройства, структурную схему надежности которых можно представить в виде отдельных компонентов, содержащих только последовательные или только параллельные соединения элементов. В таком случае расчет надежности устройства можно произвести поэтапно, объединяя на каждом этапе либо последовательно, либо параллельно соединенные элементы и заменяя их одним «обобщенным» элементом.
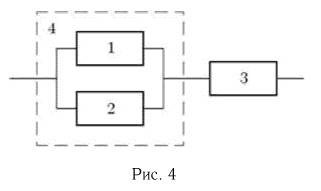
Например, пусть нужно определить вероятность отказа состоящего из трех элементов устройства, структурная схема надежности которого приведена на рис. 4. Известно, что элементы отказывают независимо друг от друга и вероятности отказов элементов 1, 2, 3 за заданное время работы равны соответственно 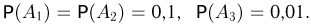 Для нахождения вероятности Р(A) отказа всего устройства заменим сначала параллельно соединенные элементы 1 и 2 «обобщенным» элементом 4, вероятность отказа которого в соответствии с приведенным ранее правилом равна
Для нахождения вероятности Р(A) отказа всего устройства заменим сначала параллельно соединенные элементы 1 и 2 «обобщенным» элементом 4, вероятность отказа которого в соответствии с приведенным ранее правилом равна
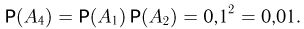
Теперь осталось заметить, что структурная схема надежности всего устройства представляет собой последовательное соединение элемента 3 и «обобщенного» элемента 4. Значит,
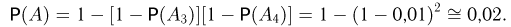
Отметим, что при вычислении вероятности отказа устройства мы фактически пользовались следующим представлением события А:
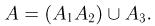
Отсюда в силу формул де Моргана для события 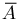 — безотказной работы устройства на заданном промежутке времени — получаем выражение
— безотказной работы устройства на заданном промежутке времени — получаем выражение
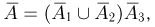
где событие 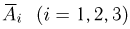 — безотказная работа i-го элемента.
— безотказная работа i-го элемента.
Решение заданий и задач по предметам:
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность

