Оглавление:
Теорема Ривальса
Для выяснения кинематического смысла переносного ускорения рассмотрим движение твердого тела относительно неподвижной системы координат Oxyz. Подвижную систему 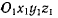 неизменно свяжем с твердым телом. В этом случае точки твердого тела не будут совершать никакого относительного движения относительно подвижной системы координат, относительная скорость и относительное ускорение этих точек будут равны нулю, и формула
неизменно свяжем с твердым телом. В этом случае точки твердого тела не будут совершать никакого относительного движения относительно подвижной системы координат, относительная скорость и относительное ускорение этих точек будут равны нулю, и формула
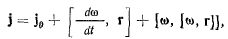
установленная Ривальсом, будет определять абсолютные ускорения точек твердого тела. Здесь 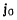 — ускорение начала подвижной
— ускорение начала подвижной
системы координат (ускорение полюса), a 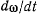 — угловое ускорение тела.
— угловое ускорение тела.
Вектор
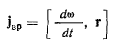
будем называть вращательным ускорением точек твердого тела.
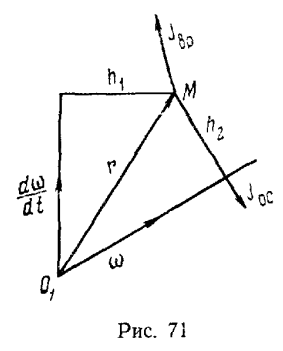
Этот вектор направлен ортогонально к плоскости, проходящей через векторы 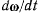 и r а его величина равна произведению модуля вектора
и r а его величина равна произведению модуля вектора 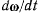 на расстояние точки М до линии действия вектора
на расстояние точки М до линии действия вектора
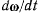 (рис. 71), т. е.
(рис. 71), т. е.
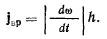
Определенное так вращательное ускорение точек твердого тела
может быть представлено теперь как касательное ускорение точки
твердого тела, вращающегося вокруг оси, совпадающей с линией
действия вектора 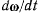
Вектор
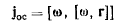
называют осестремительным ускорением точек
твердого тела. Нетрудно видеть, что вектор 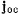 не изменяет своих
не изменяет своих
величины и направления, если переносить вектор 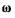 вдоль его линии
вдоль его линии
действия, т. е. если перенести начало вектора 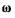 в точку, являющуюся основанием перпендикуляра, опущенного из точки М на линию действия вектора
в точку, являющуюся основанием перпендикуляра, опущенного из точки М на линию действия вектора 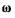 то будет иметь место равенство
то будет иметь место равенство
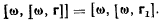
Раскрывая двойное векторное произведение, получим
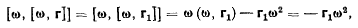
или
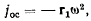
откуда видно, что вектор осестремительного ускорения направлен
по 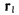 линии действия вектора
линии действия вектора 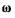 а его величина равна
а его величина равна
произведению квадрата угловой скорости вращения твердого тела на
расстояние 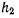 точки М от линии действия вектора
точки М от линии действия вектора 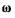 . Это ускорение
. Это ускорение
определяется так, как будто твердое тело вращается с постоянной
угловой скоростью 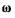 вокруг неподвижной оси, совпадающей с
вокруг неподвижной оси, совпадающей с
линией действия вектора 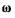 . Отсюда получаем теорему.
. Отсюда получаем теорему.
Теорема Ривальса. Ускорение произвольной точки твердого тела складывается из ускорения полюса, вращательного и осестремительного ускорений.
Пример:
Конус II с углом при вершине 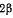 катится без скольжения
катится без скольжения
по внешней стороне неподвижного конуса I с углом при вершине 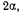 причем
причем
ось симметрии подвижного конуса вращается вокруг оси симметрии
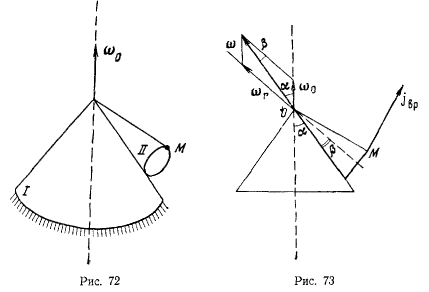
неподвижного конуса с постоянной угловой скоростью 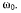 Определить абсолютное ускорение верхней точки М основания подвижного конуса, полагая, что радиус это основания равен r (рис. 72).
Определить абсолютное ускорение верхней точки М основания подвижного конуса, полагая, что радиус это основания равен r (рис. 72).
Решение:
Выберем в качестве полюса вершину конуса, остающуюся
неподвижной во все время движения. Будем иметь (рис. 73)  а ускорение точки М будет складываться из осестремительного и вращательного. Для определения этих составляющих ускорения прежде всего найдем величину и направление вектора мгновенной угловой скорости вращения подвижного конуса Нетрудно видеть, что общая образующая двух упомянутых конусов является мгновенной осью вращения подвижного конуса, поскольку точки подвижного конуса, лежащие на этой оси, имеют равные нулю скорости. Подвижный конус участвует в сложном движении. Он вращается вокруг своей оси симметрии, которая в свою очередь вращается вокруг вертикальной оси. Абсолютная угловая скорость вращения конуса равна сумме угловых скоростей переносного и относительного движений и определяется по правилу сложения векторов. Нетрудно найти н величину абсолютной угловой скорости (рис 73):
а ускорение точки М будет складываться из осестремительного и вращательного. Для определения этих составляющих ускорения прежде всего найдем величину и направление вектора мгновенной угловой скорости вращения подвижного конуса Нетрудно видеть, что общая образующая двух упомянутых конусов является мгновенной осью вращения подвижного конуса, поскольку точки подвижного конуса, лежащие на этой оси, имеют равные нулю скорости. Подвижный конус участвует в сложном движении. Он вращается вокруг своей оси симметрии, которая в свою очередь вращается вокруг вертикальной оси. Абсолютная угловая скорость вращения конуса равна сумме угловых скоростей переносного и относительного движений и определяется по правилу сложения векторов. Нетрудно найти н величину абсолютной угловой скорости (рис 73):
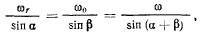
откуда получим
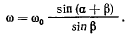
Угловое ускорение 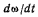 равно производной от вектора
равно производной от вектора  по времени, взятой в неподвижной системе координат Очевидно, что конец вектора
по времени, взятой в неподвижной системе координат Очевидно, что конец вектора  будет описывать окружность вокруг вертикальной оси, и скорость конца вектора » можно определить по формуле Эйлера
будет описывать окружность вокруг вертикальной оси, и скорость конца вектора » можно определить по формуле Эйлера
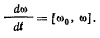
Для величины вектора 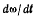 имеем условие
имеем условие
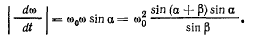
Величина вращательного ускорения определяется равенством
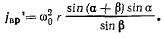
Расстояние точки М до мгновенной оси вращения
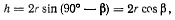
откуда для величины осестремительного ускорения получим
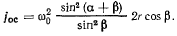
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Замечание о дифференцировании единичного вектора |
| Векторный вывод теоремы Кориолиса |
| Распределение ускорений |
| Мгновенный центр ускорений |

