Теорема об обращении функции в нуль

Теорема об обращении функции в нуль

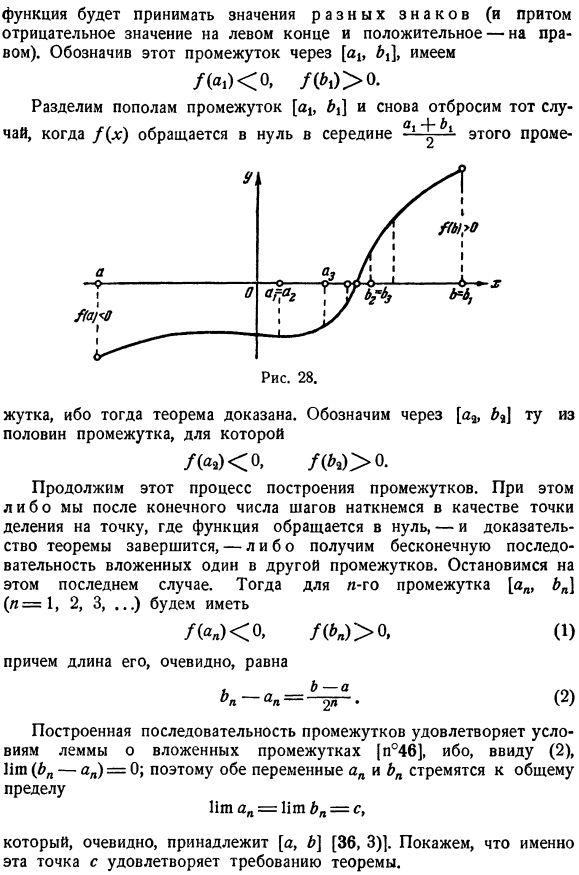
Теорема об обращении функции в нуль. Далее мы изучаем основные характеристики функции, которая непрерывна через определенные промежутки времени. Интересно, что эти свойства очередного изложения часто служат основой для различных выводов. Больцано(1817) был первым на пути их строгого оправдания, а после него был Коши(1821).Они принадлежат к следующим важным теоремам: Первая теорема Больцано-Коши. Предположим, что функция f (x) определена как непрерывная на замкнутом интервале (a, b) и принимает другое знаковое значение в конце этого интервала. Затем, между a и b, нам нужно найти точку c, в которой функция исчезает. F©= 0(а с б). (рис.28). Доказательство осуществляется методом деления интервала[N ° B1].

Теорема имеет очень простой геометрический смысл: если непрерывная кривая проходит от одной стороны оси x к другой, она пересекает эту ось. Людмила Фирмаль

• Для ясности предположим, что/(a)> 0 и/ (^)> 0. Разделите интервал[a, b \пополам на point. It может случиться. а + б Что функция f (x) исчезает в этой точке, и теорема Доказано: тогда мы можем поставить на один конец зазора ( * ) Функция принимает другое значение знака (плюс отрицательное значение слева, положительное значение справа).Этот разрыв представлен формулой [ab].、 /（、）0、/（、）> 0。 Разделите его пополам с интервалом [ab и отбросьте снова, если/(x) исчезает в середине. Это жутко, потому что теорема доказана. [А, B% указывают половину интервала /（）0、/（）> 0。 Процесс наращивания этого разрыва continues.

• В этом случае после конечного числа шагов функция будет спотыкаться как разделительная точка до точки, в которой она исчезает, и доказательство теоремы будет завершено, или она приобретет последовательность бесконечных интервалов, вложенных друг в друга. Давайте поговорим об этом последнем деле. Тогда N-й интервал[an, bn (n = 1, 2, 3,…） / S 0、/（*>»）> 0、（1） И его длина однозначно равна =(2） Построенная интервальная последовательность удовлетворяет условию вложенной интервальной леммы[n°46].Поскольку с точки зрения (2), тη (Ln-an)= 0; следовательно, существует тенденция к общему ограничению на обе переменные a и b Итн = \ \ м БН = с.

Если вы можете разложить интервал решения функции на конечное число частичных интервалов, функция называется онотонной, и каждый интервал монотонно отделен. Людмила Фирмаль

• Это, очевидно, относится к[a, b] [36, 3)].Указывает, что эта точка c точно соответствует требованиям теоремы. Достигните предела неравенства(1) и получите его одновременно, используя непрерывность функции(особенно в точке x = c). Ф©= 11м /(Аль) * B0 и F(Е)= ТМ /() >（）、 Так что на самом деле f©= 0.Теорема доказана. Заметим, что требование о непрерывности функции f (x) в замкнутых интервалах[a, b]является существенным. Функции с разрывами не менее 1 балла изменяются с отрицательных на положительные. Например, если вы используете функцию f (x)-E(x)-y, то f(0)= —y и f (1)= y (перейти на = 1), но она не будет равна нулю.

Смотрите также:

Решение задач по математическому анализу

Степенно-показательные выражения.	Применение непрерывных функций к решению уравнений.
Классификация разрывов.	Теорема о промежуточном значении.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.