Теорема о повторении опытов с примерами решения и образцами выполнения

Частная теорема о повторении опытов касается того случая, когда
вероятность события А во всех опытах одна и та же. На практике
часто приходится встречаться с более сложным случаем, когда опыты
производятся в неодинаковых условиях-, и вероятность события от
опыта к опыту меняется. Например, если производится ряд выстрелов в переменных условиях (скажем, при изменяющейся дальности), то вероятность попадания от выстрела к выстрелу может заметно меняться.

Способ вычисления вероятности заданного числа появлений
события в таких условиях дает общая теорема о повторении опытов.

Пусть производится n независимых опытов, в каждом из которых
может появиться или не появиться некоторое событие А, причем
вероятность появления события А в і-м опыте равна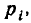, а вероятность непоявления 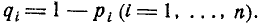Требуется найти вероятность 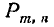а того, что в результате п опытов событие А появится ровно m раз.

Обозначим по-прежнему 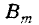событие, состоящее в том, что событие А появятся m раз в n опытах. По-прежнему представим 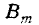как
сумму произведений элементарных событий:

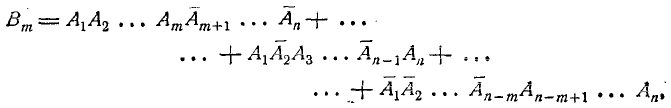
т. е. искомая вероятность равна сумме всех возможных произведений,
в которые буквы р с разными индексами входят m раз, а буквы q
с разными индексами n — m раз.

Для того чтобы чисто механически составлять все возможные
произведения из m букв p и n — m букв q с разными индексами,
применим следующий формальный прием. Составим произведение n
биномов:

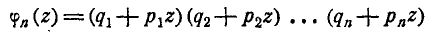
или короче

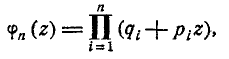
где z — произвольный параметр.

Зададимся целью найти в этом произведении биномов
коэффициент при 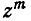. Для этого перемножим биномы и произведем приведение подобных членов. Очевидно, каждый член, содержащий 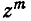, будет иметь в качестве коэффициента произведение m букв n
с какими-то индексами и n—m букв q, а после приведения
подобных членов коэффициент при 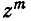будет представлять собой сумму всех возможных произведений такого типа. Следовательно, способ составления этого коэффициента полностью совпадает со способом вычисления вероятности 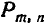в задаче о повторении опытов.

Функция 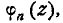, разложение которой по степеням параметра z дает в качестве коэффициентов вероятности 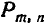, называется производящей функцией вероятностей 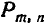или просто производящей функцией.

Пользуясь понятием производящей функции, можно сформулировать общую теорему о повторении опытов в следующем виде.
Вероятность того, что событие А в n независимых опытах
появится ровно т раз, равна коэффициенту при 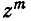в выражении
производящей функции:

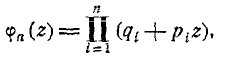
где Pi — вероятность появления события А в i-м опыте,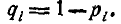

Вышеприведенная формулировка общей теоремы о повторении
опытов в отличие от частной теоремы не дает явного выражения
для вероятности 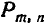. Такое выражение в принципе написать можно, но оно является слишком сложным, и мы не будем его приводить. Однако, не прибегая к такому явному выражению, все же можно записать общую теорему о повторении опытов в виде одной
формулы:

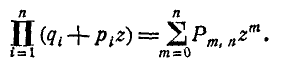
Левая и правая части равенства (4.2.1) представляют собою одну
!ту же производящую функцию 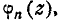только слева она написана
виде одночлена, а справа — в виде многочлена. Раскрывая скобки
левой части и выполняя приведение подобных членов, получим все
вероятности:

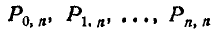
как коэффициенты соответственно при нулевой, первой и т. д. степенях z.

Очевидно, частная теорема о повторении опытов вытекает из
общей при

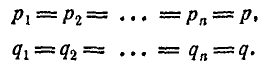
В этом случае производящая функция обращается в n-ю степень
бинома (q + pz):

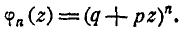
Раскрывая это выражение по формуле бинома, имеем: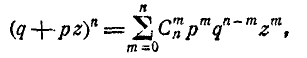

откуда следует формула (4.1.1).

Отметим, что как в общем, так и в частном случае сумма всех
вероятностей 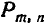равна единице:

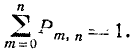(4.2.2)

Это следует прежде всего из тою, что события Во, В1, … Вn
образуют полную группу несовместных событий. Формально к равен-
равенству (4.2.2) можно прийти, полагая в общей формуле (4.2.1) z = 1.

Во многих случаях практики, кроме вероятности 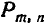ровно m.
появлений события А, приходится рассматривать вероятность и не
менее m появлений события А.

Обозначим 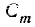событие, состоящее в том, что событие А поя-
появится не менее m раз, а вероятность события 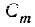обозначим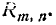

Очевидно,

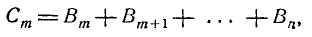
откуда, по теореме сложения,

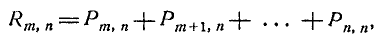
или короче

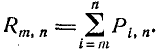(4.2.3)

При вычислении 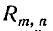часто бывает удобнее не пользоваться
непосредственно формулой (4.2.3), а переходить к противоположному
событию и вычислять вероятность 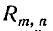по формуле 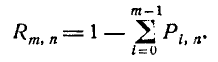(4.2.4)

Пример:

Производится 4 независимых выстрела по одной и той же
цели с различных расстояний; вероятности попадания при этих выстрелах равны соответственно

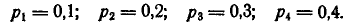
Найти вероятности ни одного, одного, двух, трех и четырех попаданий:

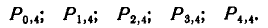
Решение:

Составляем производящую функцию:

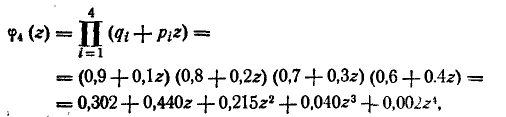
откуда

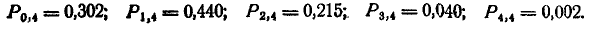
Пример:

Производится 4 независимых выстрела в одинаковых
условиях, причем вероятность попадания р есть средняя из вероятностей р1, р2, p3 и P4 предыдущего примера: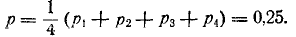

Найти вероятности

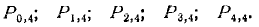
Решение:

По формуле (4.1.1) имеем

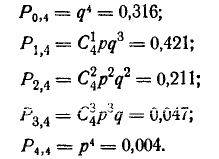
Пример:

Имеется 5 станций, с которыми поддерживается связь.
Время от времени связь прерывается из-за атмосферных помех. Вследствие удаленности станций перерыв друг от друга связи с каждой из них происходит независимо от остальных с вероятностью р = 0,2. Найти вероятность того, что в данный момент времени будет иметься связь не более чем с двумя станциями.

Решение:

Событие, о котором идет речь, сводится к тому, что будет
нарушена связь не менее чем с тремя станциями. По формуле (4.2.3)
получим:

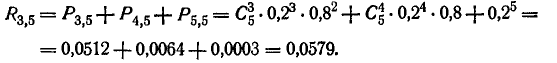
Пример:

Система радиолокационных станций ведет наблюдение за группой объектов, состоящей из 10 единиц. Каждый из объектов может быть (независимо от других) потерян с вероятностью 0,1. Найти вероятность того, что хотя бы один из объектов будет потерян.

Решение:

Вероятность потери хотя бы одного объекта 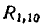можно
было бы найти по формуле

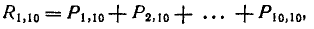
но несравненно проще воспользоваться вероятностью противоположного события — ни один объект не потерян — и вычесть ее из единицы:

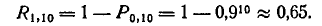
Пример:

Прибор состоит из 8 однородных элементов, но может
работать при наличии в исправном состоянии не менее 6 из них. Каждый из элементов за время работы прибора t выходит из строя независимо от других с вероятностью 0,2. Найти вероятность того, что прибор откажет за время t.

Решение:

Для отказа прибора требуется выход из строя не менее
двух из восьми элементов. По формуле (4.2.4) имеем: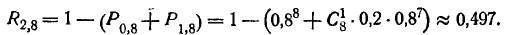

Пример:

Производится 4 независимых выстрела с самолета по
самолету. Вероятность попадания при каждом выстреле равна 0,3. Для поражения (выхода из строя) самолета заведомо достаточно двух попаданий; при одном попадании самолет поражается с вероятностью 0,6. Найти вероятность того, что самолет будет поражен.
Решение:

Задача решается по формуле полной вероятности. Можно
было бы рассмотреть гипотезы

Н1—в самолет попал 1 снаряд,
Н2 — в самолет попало 2 снаряда,
Н3 — в самолет попало 3 снаряда.
H4 — в самолет попало 4 снаряда

и находить вероятность события А — поражения самолета — с помощью этих четырех гипотез. Однако значительно проще рассмотреть всего две гипотезы:

Но — в самолет не попало ни одного снаряда,
H1 — в самолет попал 1 снаряд,

и вычислять вероятность события 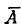— непоражения самолета: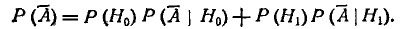

Имеем:

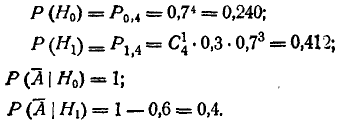
Следовательно,

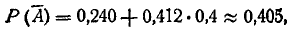
откуда

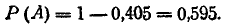
Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Статистическое исследование зависимостей
9. Теории игр
10. Вероятность события
11. Теорема умножения вероятностей
12. Формула полной вероятности
13. Нормальный закон распределения
14. Определение законов распределения случайных величин на основе опытных данных
15. Системы случайных величин
16. Нормальный закон распределения для системы случайных величин
17. Вероятностное пространство
18. Классическое определение вероятности
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность