Теорема Ляпунова

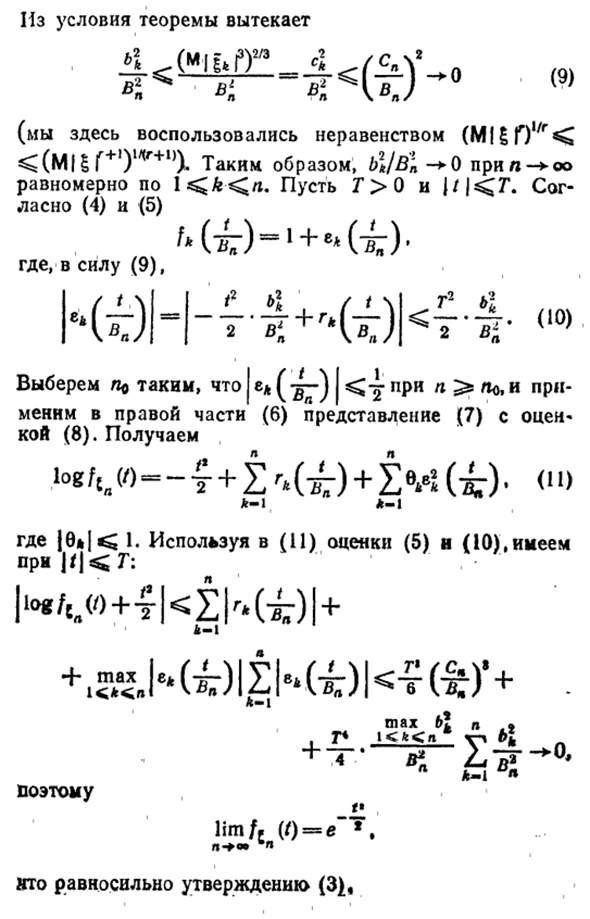
Теорема Ляпунова

• Теорема Ляпунова Центральная предельная теорема также выполняется при определенных условиях с неравными независимыми условиями. Далее мы докажем эту теорему с помощью уравнения Ляпунова.

• Здесь k = 1 и 2 независимы, поэтому они не всегда имеют одинаковое распределение. шоу Mlk = akt D b = M | b-fli’f —cj 4. —Bl ^ Ybl d = Zcj. Fe-я Теорема 2. (Теорема Ляпунова.) Если gie «♦ • независима, a * и c * конечны и Cn / Bn — * — 0, im R {6 | + — <= ФОт). (3) — так что я * -> ОО Доказательство.

Установите Ik ^ lk- & k> fk (1) = * flh (t). Людмила Фирмаль

• Поскольку M | * = 0, -MC ^ — * ® ) Следуй за этим (7) Где | jc | ^ 1/2 | в () | Z * -1 (8) к-2 Гипотеза теоремы B \ (Mitfc I3) 273 с \ / Cn \ 2 (Использованное неравенство (M | £ f) l / r < <(M | ^ Γ +,) М ++ 1) X Следовательно, bl / B * n-►Ofor- ^ oo равномерно в 1 ^ .k ^ n. Γ> 0 и | / | <7 \ согласно (4) и (5)

Где, благодаря (9), КЯН-ИЧ0 | <У- «0) | E ｜ (| есть η> Λ0, и применить выражение (7) с оценочным значением (8) справа от (6). bghaw ■ — m + i * w + b «w. Где, используя оценки (5) и (10) из 1. (11), для << | <7-: Максимум р G * K * <* V P Таким образом, II P- * op »P

Это эквивалентно утверждению (3)> Людмила Фирмаль

Смотрите также:

Решение задач по математической статистике

Теорема о непрерывном соответствии между множеством характеристических функций и множеством функций распределения	Применения центральной предельной теоремы
Центральная предельная теорема для одинаково распределенных независимых слагаемых	Определение и простейшие свойства

Если вам потребуется заказать решение математической статистики вы всегда можете написать мне в whatsapp.