Температурные и монтажные напряжения в статически неопределимых системах

Температурные и монтажные напряжения в статически неопределимых системах

• Нагрев или охлаждение статической неопределенной системы в пределах температурных и монтажных напряжений элементов статической неопределенной системы геометрические размеры элементов мешают опорным соединениям, например, статически

определяемому стержню(фиг. 17.4, а) при нагревании его размеры увеличиваются, и поперечное сечение с смещается вправо на AC/. При нагревании статически неопределенный стержень(рис. 17.4, Б) продольное перемещение секции с предотвращается жесткой опорой, что приводит к появлению внутренних продольных сил в ее поперечном сечении.

Кроме того, дополнительное давление Людмила Фирмаль

(монтажное давление)в статически неопределенной системе обусловлено неправильным изготовлением длин отдельных элементов при сборке. Температурные и установочные напряжения статически неопределенной системы определяются таким же образом, как и расчеты силовой нагрузки. Например. Может быть. 17.5, a, / = нагретый до температуры 25°, og с диаграммой Y.

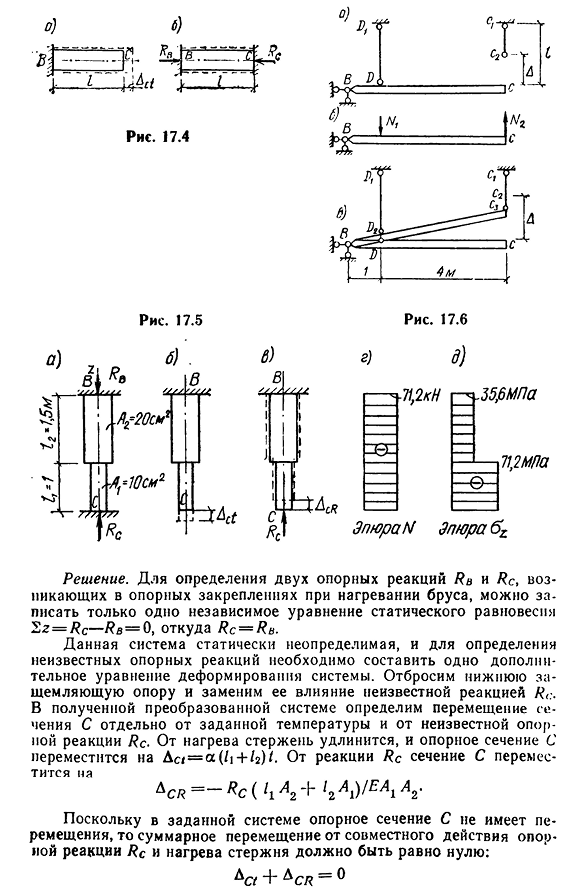
коэффициент расширения линии a=10-5 и E=2″105MPa. 170i) В J-I Рис 17.4 Решение. Только одно независимое уравнение статического равновесия’2z=R c-Rb=0, где Rc=Rb, определяет две опорные реакции Rb и Rc, которые происходят в опорном фиксирующем приспособлении при нагреве балки Эта система статически неопределима, и для того, чтобы определить неизвестную реакцию опоры, необходимо составить одно дополнительное уравнение

• деформации системы. Отбросьте поддержку Пинча ниже и замените этот эффект неизвестной реакцией R (:. В полученной системе преобразования смещение секции с определялось отдельно от заданной температуры и неизвестной эталонной реакции RC. От нагрева стержень удлиняется, и опорная секция C перемещается в положение DS / =a (/1 + /2)/. От реакции Rc поперечное сечение C перемещается к DSL= — M’1L2+1ga1ueaga2- В данной системе отсчетное сечение с не имеет смещения, поэтому полное смещение от действия

соединения отсчетного реактора Rc и нагрева стержня должно быть равно нулю. Сто семьдесят один «(‘i+Y T D2+12A^ / EA, A2=0, А где же босс?= 10-5 (1 + 1,5) 2 5 -2 .1 (U-10″. 10». «Ю»-20-10-4 B2 0 -1 0 -* + 1 ,5 .1-0. -* Продольная сила N во всех сечениях балки одинакова и равна N=-71,2 кн(рис. 17.5, г). Нормальные напряжения всех поперечных сечений также сжимаются. Сюжет Оз показан на рисунке. 17.5, д. Например. В системе, указанной в RNS. 17.6, a, стержень C\C2 определяет внутренние силы, возникающие в стержне DDi и C\C2 после сборки системы. Решение. Для сборки этой системы необходимо растянуть стержень C2 усилием N2. Но в то же время в стержне DD\сила

сжатия Nj(рис. 17.6, 6). Давайте создадим состояние равновесия для системы.: = = = Nx=5N2, (17.6) из этого уравнения невозможно определить две Людмила Фирмаль

внутренние силы M и N2. Для решения этой задачи необходимо построить дополнительное уравнение из деформационного состояния системы. После сборки системы путем растяжения стержня C\C2 жесткий стержень перемещается вверх (поворачивается вокруг шарнира B) и занимает некоторые положения BD2C3( 17.6, b). В этом случае полоса CiC2 удлиняется на величину C2C3=N2IIEA. Уравнение перемещения стержня SS\выглядит следующим образом(Рис. 17.6, b): SS3+C2C3=D или SS3=D-N2l/EAi. Связь между движениями SS3 и DD2

устанавливается из подобия треугольников BDD2 и BSS3: DD2=SS3 / 5 или Nx1 / 2)=(D-Nx l / E A J / 5. (17.7) если мы решим уравнение (17.6) и (17.7) вместе, то получим N1==A E a l/0t7l и N2=AZL4j/3,5 Z. Знак плюс перед значениями Ni и N2 указывает на то, что DDI-стержень сжат, а CCi-стержень растянут, то есть совпадает с предварительным предположением.

Смотрите также:

Решение задач по технической механике

Диаграмма сжатия	Основные понятия и расчетные схемы сооружений
Сложение пар, лежащих в одной плоскости.Условие равновесия плоской системы пар	Допущения и ограничения, принятые в сопротивлении материалов

Если вам потребуется помощь по технической механике вы всегда можете написать мне в whatsapp.