Оглавление:

| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как получить помощь в выполнении заданий по технической механике
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько стоит помощь
Стоимость помощи зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения
Минимальный срок выполнения составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения действует гарантия. В течении 1 года я и моя команда исправим любые ошибки.
Чуть ниже я предоставила лекции по всем темам предмета техническая механика, чтобы вы смогли подготовиться к сдаче заказанной у меня работы, так как иногда преподаватели спрашивают теорию.
Основные понятия и аксиомы статики
Техническая механика — комплексная дисциплина. Она включает три раздела: «Теоретическая механика», «Сопротивление материалов», «Детали машин». «Теоретическая механика» — раздел, в котором излагаются основные законы движения твердых тел и их взаимодействия. В разделе «Сопротивление материалов» изучаются основы прочности материалов и методы расчетов элементов конструкций на прочность, жесткость и устойчивость под действием внешних сил. В заключительном разделе «Технической механики» «Детали машин» рассматриваются основы конструирования и расчета деталей и сборочных единиц общего назначения.
Дисциплина «Техническая механика» является общепрофсссиональной, обеспечивающей базовые знания при усвоении специальных дисциплин, изучаемых в дальнейшем. Задачи теоретической механики
Техническая механика — наука о механическом движении материальных твердых тел и их взаимодействии. Механическое движение понимается как перемещение тела в пространстве и во времени по отношению к другим телам, в частности к Земле.
Для удобства изучения теоретическую механику подразделяют на статику, кинематику и динамику.
Статика изучает условия равновесия тел под действием сил.
Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются. Динамика изучает движение тел под действием сил.
В отличие от физики теоретическая механика изучает законы движения некоторых абстрактных абсолютно твердых тел: здесь материалы, форма тел существенного значения не имеют. При движении абсолютно твердое тело не деформируется и не разрушается. В случае, когда размерами тела можно пренебречь, тело заменяют материальной точкой. Это упрощение, принятое в теоретической механике, значительно облегчает решение задач о движении. Понятие о силе и системе сил
Сила — это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т.е. сила есть величина векторная характеризующаяся точкой приложения (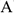 ), направлением (линией действия), величиной (модулем) (рис. 1.1).
), направлением (линией действия), величиной (модулем) (рис. 1.1).
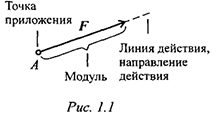
Силу измеряют в ньютонах,
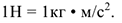
Силы, действующие на тело (или систему тел), делятся на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.
Внутренние силы возникают в теле под действием внешних сил. Совокупность сил, действующих на какое-либо тело, называют системой сил. Эквивалентная система сил — система сил, действующая так же, как заданная. Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.
Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.
Возможно эта страница вам будет полезна:
| Предмет техническая механика |
Аксиомы статики
В результате обобщения человеческого опыта были установлены общие закономерности механического движения, выраженные в виде законов и теорем. Все теоремы и уравнения статики выводятся из нескольких исходных положений. Эти положения называют аксиомами статики.
Первая аксиома
Под действием уравновешенной системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).
Вторая аксиома
Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются (рис. 1.2).
Третья аксиома
Не нарушая механического состояния тела, можно добавить или убрать уравновешенную систему сил (принцип отбрасывания системы сил, эквивалентной нулю) (рис. 1.3).
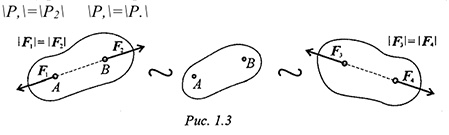
Четвертая аксиома (правило параллелограмма сил)
Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах (рис. 1.4).
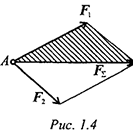
Вместо параллелограмма можно построить треугольник сил: силы вычерчивают одну за другой в любом порядке; равнодействующая двух сил соединяет начало первой силы с концом второй.
Пятая аксиома
При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие (рис. 1.5). Силы действующие и противодействующие всегда приложены к разным телам, поэтому они не уравновешиваются .
Силы, с которыми два тела действуют друг на друга, всегда равны по модулю и направлены вдоль одной прямой в разные стороны.
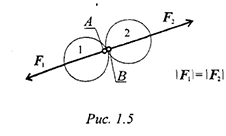
Следствие из второй и третьей аксиом
Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия (рис. 1.6).
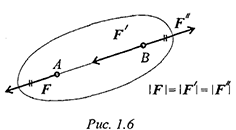
Сила 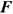 приложена в точке
приложена в точке 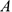 . Требуется перенести ее в точку
. Требуется перенести ее в точку 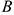 . Используя третью аксиому, добавим в точке
. Используя третью аксиому, добавим в точке 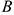 уравновешенную систему сил
уравновешенную систему сил 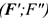
Образуется уравновешенная по второй аксиоме система сил 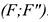 . Убираем ее и получим в точке
. Убираем ее и получим в точке 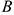 силу
силу 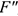 , равную заданной
, равную заданной 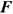 .
.
Связи и реакции связей
Все законы и теоремы статики справедливы для свободного твердого тела.
Все тела делятся на свободные и связанные.
Свободные тела — тела, перемещение которых не ограничено.
Связанные тела — тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещение других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться. Всякое связанное тело можно представить свободным, если
связи заменить их реакциями (принцип освобождения от связей). Все связи можно разделить на несколько типов.
Связь — гладкая опора (без трения)
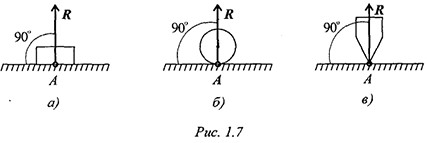
Реакция опоры приложена в точке опоры и всегда направлен перпендикулярно опоре (рис. 1.7).
Гибкая связь (нить, веревка, трос, цепь)
Груз подвешен на двух нитях (рис. 1.8).
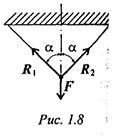
Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень
На схемах стержни изображают толсто сплошной линией (рис. 1.9).
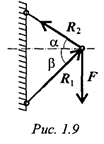
Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убирая стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называет? такое бесконечно малое мысленное перемещение, которое допускается в данный момент наложенными на него связями. Убираем стержень 1, в этом случае стержень 2 падает вниз. Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка 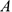 опускается вниз, отодвигаясь а стены. Следовательно, реакция стержня 2 направлена к стене.
опускается вниз, отодвигаясь а стены. Следовательно, реакция стержня 2 направлена к стене.
Шарнирная опора
Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир
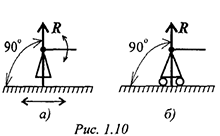
Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки) (рис. 1.10).
Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, т. к. не допускается только перемещение поперек опорной поверхности.
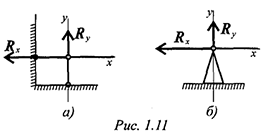
Неподвижный шарнир
Точка крепления перемещаться не может. Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее принято изображать в виде двух составляющих: горизонтальной и вертикальной 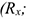
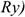 (рис. 1.11).
(рис. 1.11).
Защемление или «заделка»
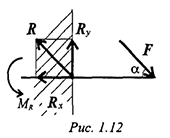
Любые перемещения точки крепления невозможны. Под действием внешних сил в опоре возникают реактивная сила и реактивный момент 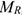 , препятствующий повороту (рис. 1.12). Реактивную силу принято представлять в виде двух составляющих вдоль осей координат
, препятствующий повороту (рис. 1.12). Реактивную силу принято представлять в виде двух составляющих вдоль осей координат
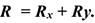
Плоская система сходящихся сил. Определение равнодействующей геометрическим способом
Знать геометрический способ определения равнодействующей системы сил, условия равновесия плоской системы сходящихся сил.
Уметь определять равнодействующую, решать задачи на равновесие в геометрической форме.
Плоская система сходящихся сил
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся (рис. 2.1).
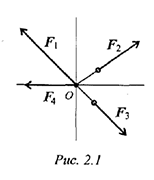
Необходимо определить равнодействующую системы сходящихся сил 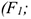
 — число сил, входящих в систему.
— число сил, входящих в систему.
По следствию из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными в одной точке.
Равнодействующая сходящихся сил
Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (вис. 2.2).
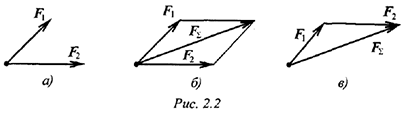
Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3).
Вектор равнодействующей силы соединит начало первого вектора с концом последнего.
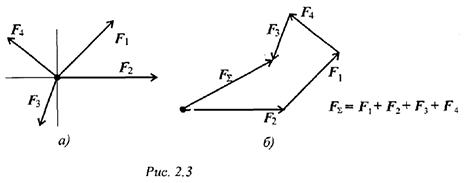
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится. Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называют геометрическим.
Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующим векторам сил.
Порядок построения многоугольника сил
- Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпадал с началом последующего.
- Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
- При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил
При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
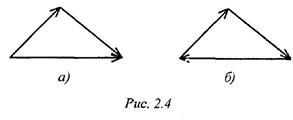
Если в системе гри силы, образуется треугольник сил.
Сравните два треугольника сил (рис. 2.4) и сделайте вывод о количестве сил, входящих в каждую систему. Рекомендация. Обратить внимание на направление векторов.
Решение задач на равновесие геометрическим способом
Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим). Порядок решения задач:
- Определить возможное направление реакций связей.
- Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура.)
- Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
- Для уточнения решения рекомендуется определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.
Пример 1.
Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 2.5а).
Решение
- Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис. 2.5а).
Определяем возможные направления реакций связей «жесткие стержни».
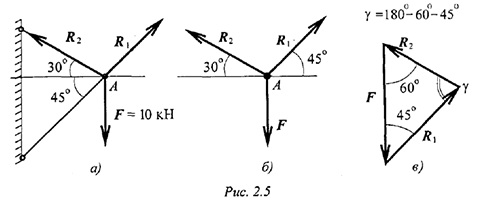
Усилия направлены вдоль стержней.
- Освободим точку
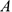 от связей, заменив действие связей их реакциями (рис. 2.5б).
от связей, заменив действие связей их реакциями (рис. 2.5б). - Система находится в равновесии. Построим треугольник сил. Построение начнем с известной силы, вычертив вектор
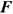 в некотором масштабе.
в некотором масштабе.
Из концов вектора 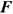 проводим линии, параллельные реакциям
проводим линии, параллельные реакциям 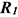 и
и 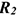 .
.
Пересекаясь, линии создадут треугольник (рис. 2.5в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях.
- Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная.
Для данного случая:
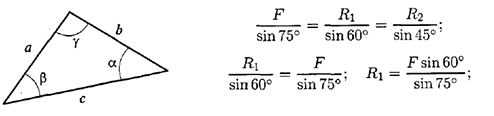
Плоская система сходящихся сил. Определение равнодействующей аналитическим способом
Знать аналитический способ определения равнодействующей силы, условия равновесия плоской сходящейся системы сил в аналитической форме. Уметь определять проекции силы на две взаимно перпендикулярные оси решать задачи на равновесие в аналитической форме.
Проекция силы на ось
Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 3.1).
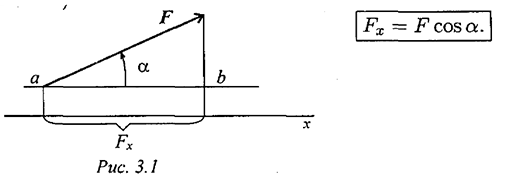
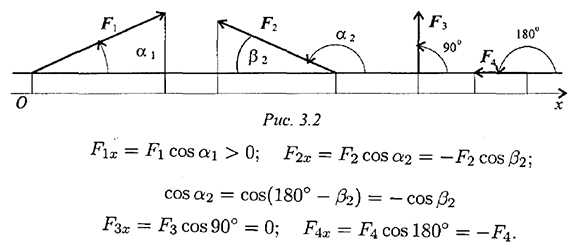
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).
Проекция силы на две взаимно перпендикулярные оси (рис. 3.3).
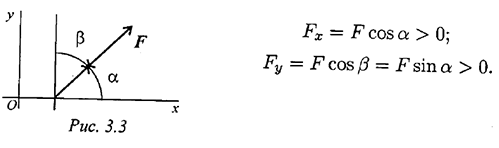
Определение равнодействующей системы сил аналитическим способом
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геометрическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси (рис. 3.4а). Складываем проекции всех векторов на оси 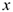 и
и 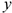 (рис. 3.4б).
(рис. 3.4б).
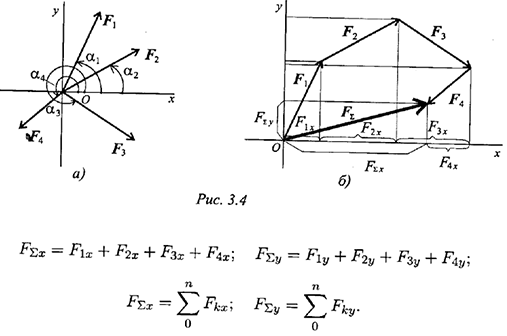
Модуль (величину) равнодействующей можно найти по известным проекциям:
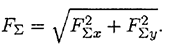
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующей с осями координат (рис. 3.5).
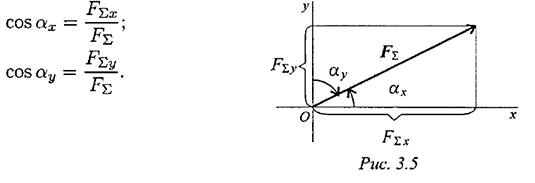
Условия равновесия плоской системы сходящихся сил в аналитической форме
Исходя из того, что равнодействующая равна нулю, получим:
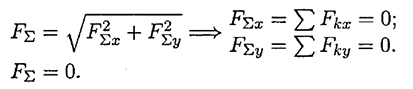
Условия равновесия в аналитической форме можно сформулировать следующим образом: Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской сходящейся системы сил:
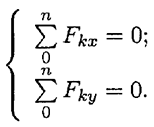
В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
Пара сил и момент силы относительно точки
Знать обозначение, модуль и определение моментов пары сил и силы относительно точки, условия равновесия системы пар сил.
Уметь определять моменты пар сил и момент силы относительно точки, определять момент результирующей пары сил.
Пара сил, момент пары сил
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.
Рассмотрим систему сил 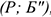 , образующих пару.
, образующих пару.
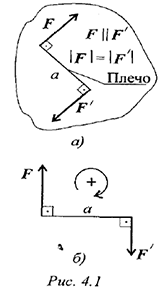
Пара сил вызывает вращение тела и ее действие на тело оценивается моментом. Силы, входящие в пару, не уравновешиваются, т. к. они приложены к двум точкам (рис. 4.1).
Их действие на тело не может быть заменено одной силой (равнодействующей).
Момент пары сил численно равен произведению модуля силы на расстояние между линиями действия сил (плечо пары). Момент считают положительным, если пара вращает тело по часовой стрелке (рис. 4.1(б)):
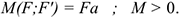
Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.
Свойства пар (без доказательств):
- Пару сил можно перемещать в плоскости ее действия.
- Эквивалентность пар. Две пары, моменты которых равны, (рис. 4.2) эквивалентны (действие их на тело аналогично).
- Сложение пар сил. Систему пар сил можно заменить равнодействующей парой.
Момент равнодействующей пары равен алгебраической сумме моментов пар, составляющих систему (рис. 4.3):
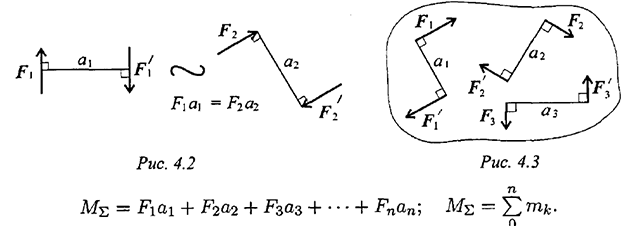
- Равновесие пар.
Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар системы равнялась нулю:
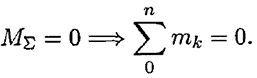
Момент силы относительно точки
Сила, не проходящая через точку крепления тела, вызывает вращение тела относительно точки, поэтому действие такой силы на тело оценивается моментом.
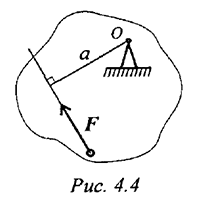
Момент силы относительно точки численно равен произведению модуля силы на расстояние от точки до линий действия силы. Перпендикуляр, опущенный из точки на линию действия силы (рис. 4.4), называется плечом силы. Обозначение момента 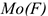 ) или
) или 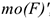 ,
,
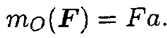
Единица измерения 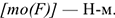
Момент считается положительным, если сила разворачивает тело по часовой стрелке.
Плоская система произвольно расположенных сил
Иметь представление о главном векторе, главном моменте, равнодействующей плоской системы произвольно расположенных сил.
Знать теорему Пуансо о приведении силы к точке, приведение произвольной плоской системы сил к точке, три формы уравнений равновесия.
Уметь заменять произвольную плоскую систему сил одной силой и одной парой.
Теорема Пуансо о параллельном переносе сил
Силу можно перенести параллельно линии ее действия, при этом нужно добавить пару сил с моментом, равным произведению модуля силы на расстояние, на которое перенесена сила.
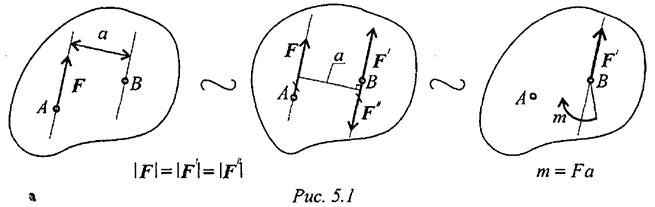
Дано: сила в точке 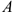 (рис. 5.1).
(рис. 5.1).
Добавим в точке 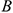 уравновешенную систему сил
уравновешенную систему сил 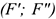 . Образуется пара сил
. Образуется пара сил 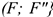 . Получим силу в точке
. Получим силу в точке 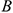 и момент пары
и момент пары 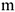
Приведение к точке плоской системы произвольно расположенных сил
Линии действия произвольной системы сил не пересекаются в одной точке, поэтому для оценки состояния тела такую систему следует упростить. Для этого все силы системы переносят в одну произвольно выбранную точку — точку приведения. Применяют теорему Пуансо. При любом переносе силы в точку, не лежащую на линии ее действия, добавляют пару сил. Появившиеся при переносе пары называют присоединенными парами. Дана плоская система произвольно расположенных сил (рис. 5.2).
Переносим все силы в точку 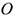 . Получим пучок сил в точке
. Получим пучок сил в точке 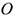 , который можно заменить одной силой — главным вектором системы. Образующуюся систему пар сил можно заменить одной эквивалентной парой — главным моментом системы.
, который можно заменить одной силой — главным вектором системы. Образующуюся систему пар сил можно заменить одной эквивалентной парой — главным моментом системы.
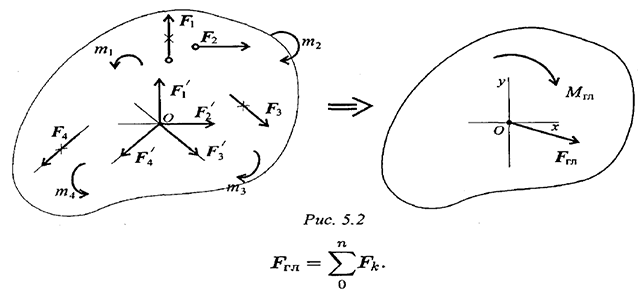
Главный вектор равен геометрической сумме векторов произвольной плоской системы сил. Проецируем все силы системы на оси координат и, сложив соответствующие проекции на оси, получим проекции главного вектора.
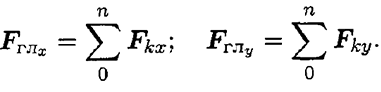
По величине проекций главного вектора на оси координат находим модуль главного вектора:
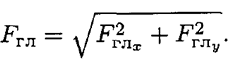
Главный момент системы сил равен алгебраической сумме моментов сил системы относительно точки приведения.
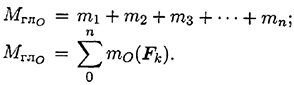
Таким образом, произвольная плоская система сил приводится к одной силе (главному вектору системы сил) и одному моменту (главному моменту системы сил).
Влияние точки приведения
Точка приведения выбрана произвольно. При изменении положения точки приведения величина главного вектора не изменится.
Величина главного момента при переносе точки приведения изменится, т. к. меняются расстояния от векторов-сил до новой точки приведения.
С помощью теоремы Вариньона о моменте равнодействующей можно определить точку на плоскости, относительно которой главный момент равен нулю. Тогда произвольная плоская система сил может быть заменена одной силой. Эту силу называют равнодействующей системы сил.
Численно равнодействующая равна главному вектору системы сил, но приложена в другой точке, относительно которой главный момент равен нулю. Равнодействующую принято обозначать. 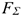 Численно ее значение определяется так же, как главный вектор системы сил:
Численно ее значение определяется так же, как главный вектор системы сил:
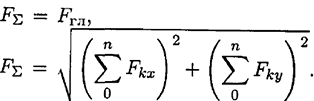
Точку приложения равнодействующей можно определить по формуле
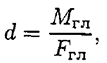
где 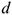 — расстояние от выбранной точки приведения до точки приложения равнодействующей;
— расстояние от выбранной точки приведения до точки приложения равнодействующей; 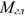 — величина главного момента относительно выбранной точки приведения;
— величина главного момента относительно выбранной точки приведения; 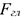 — величина главного вектора системы сил.
— величина главного вектора системы сил.
Частные случаи приведения системы сил к точке
При приведении системы сил к точке возможны следующие варианты:

тело вращается вокруг неподвижной оси. тело движется прямолинейно ускоренно, тело находится в равновесии.
Условие равновесия произвольной плоской системы сил
- При равновесии главный вектор системы равен нулю . Аналитическое определение главного вектора приводит к выводу:
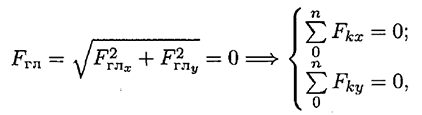
где 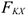 и
и 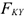 — проекции векторов на оси координат.
— проекции векторов на оси координат.
- Поскольку точка приведения выбрана произвольно, ясно, что при равновесии сумма моментов сил системы относительно любой точки на плоскости должна равняться нулю:
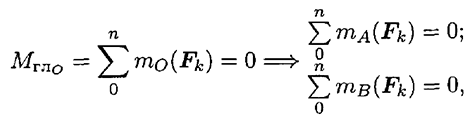
где 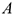 к
к 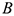 — разные точки приведения.
— разные точки приведения.
Условие равновесия произвольной плоской системы сил может быть сформулировано следующим образом:
Для того чтобы твердое тело под действием произвольной плоской системы сил находилось в равновесии, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил системы на любую ось равнялась нулю и алгебраическая сумма моментов всех сил системы относительно любой точки в плоскости действия сил равнялась нулю. Получим основную форму уравнения равновесия:
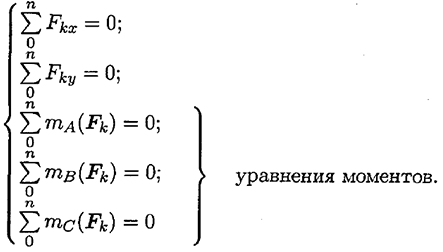
Теоретически уравнений моментов можно записать бесконечное множество, но практически доказано, что на плоскости можно составить только три независимых уравнения моментов и при этом три точки (центры моментов) не должны лежать на одной линии. Таким образом, имеем пять независимых уравнений равновесия.
Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным. Для разных случаев используются три группы уравнений равновесия.

Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия
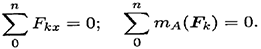
Ось 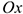 системы координат параллельна линии действия сил.
системы координат параллельна линии действия сил.
Возможно эта страница вам будет полезна:
| Примеры решения задач технической механике |
Балочные системы. Определение реакций опор и моментов Защемления
Иметь представление о видах опор и возникающих реакциях в опорах.
Знать три формы уравнений равновесия и уметь их использовать для определения реакций в опорах балочных систем. Уметь выполнять проверку правильности решения.
Виды нагрузок и разновидности опор
Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.
В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).
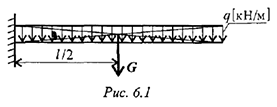
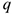 — интенсивность нагрузки;
— интенсивность нагрузки; 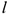 — длина стержня;
— длина стержня;
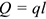 — равнодействующая распределенной нагрузки. Рис. 6.1 Разновидности опор балочных систем (см. лекцию 1)
— равнодействующая распределенной нагрузки. Рис. 6.1 Разновидности опор балочных систем (см. лекцию 1)
Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами. Высота сечения балки незначительна по сравнению с длиной. Жесткая заделка (защемление) (рис.6.2)
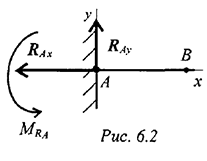
Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы 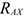 и
и 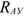 и парой с моментом
и парой с моментом 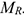 .
.
Для определения этих неизвестных удобно использовать систему уравнений в виде
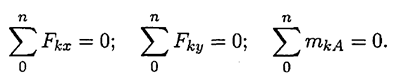
Каждое уравнение имеет одну неизвестную величину и решается без подстановок.
Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например 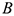 :
:
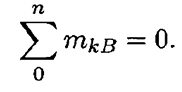
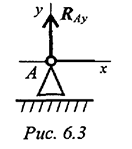
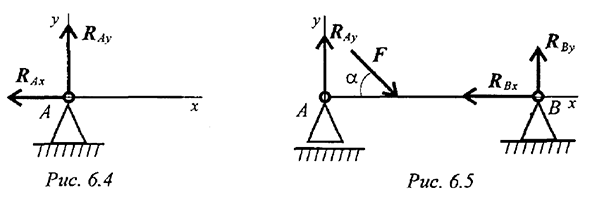
Шарнирпо-подвижная опора (рис. 6.3) Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности. Шарнирно-неподвижная опора (рис. 6.4)
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
Балка на двух шарнирных опорах (рис. 6.5)
Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:
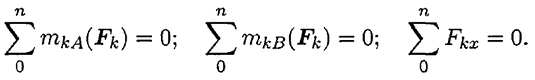
Составляются уравнения моментов относительно точек крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.
Из уравнения 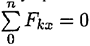 определяется реакция
определяется реакция 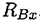 .
.
Из уравнения 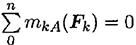 определяется реакция
определяется реакция 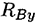 .
.
Из уравнения 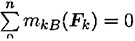 определяется реакция
определяется реакция 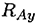 .
.
Для контроля правильности решения используется дополнительное уравнение
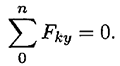
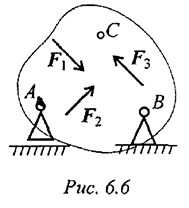
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):
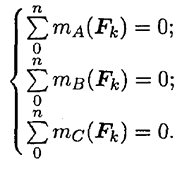
Пространственная система сил
Знать момент силы относительно оси, свойства моменте аналитический способ определения равнодействующей, условия равновесия пространственной системы сил.
Уметь выполнять разложение силы на три взаимно перпендикулярные оси, определять момент силы относительно оси.
Пространственная система сил — система сил, линии действия которых не лежат в одной плоскости.
Момент силы относительно оси
Момент силы относительно оси равен моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью (рис. 7.1 а).
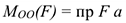
 — расстояние от оси до проекции
— расстояние от оси до проекции 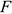 ;
;
пр 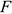 — проекция силы на плоскость, перпендикулярную оси
— проекция силы на плоскость, перпендикулярную оси 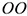 .
.
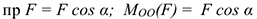
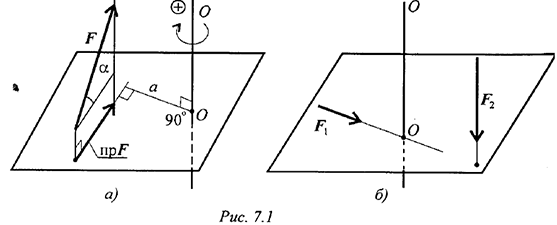
Момент считаем положительным, если сила разворачивает тело по часовой стрелке. Смотреть со стороны положительного направления оси.
Если линия действия силы пересекает ось или линия действия силы параллельна оси, моменты силы относительно этой оси равны нулю (рис. 7.16).
Силы и ось лежат в одной плоскости, они не смогут повернуть тело вокруг этой оси. 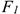 пересекает ось;
пересекает ось; 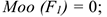
Пространственная сходящаяся система сил
Вектор в пространстве
В пространстве вектор силы проецируется на три взаимно перпендикулярные оси координат. Проекции вектора образуют ребра прямоугольного параллелепипеда, вектор силы совпадает с диагональю (рис. 7.2).
Модуль вектора может быть получен из зависимости
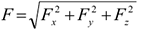
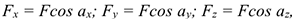
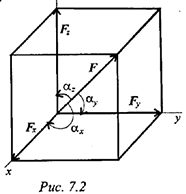
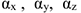 — углы между вектором
— углы между вектором 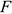 и осями координат.
и осями координат.
Пространственная сходящаяся система сил
Пространственная сходящаяся система сил — система сил, не лежащих в одной плоскости, линии действия которых пересекаются в одной точке.
Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник (рис. 7.3),
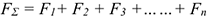
Доказано, что равнодействующая системы сходящихся сил приложена в точке пересечения линий действия сил системы.
Модуль равнодействующей пространственной системы сходящихся сил можно определить аналитически, использовав метод проекций.
Совмещаем начало координат с точкой пересечения линий действия сил системы. Проецируем все силы на оси координат и суммируем соответствующие проекции (рис. 7.4). Получим проекции равнодействующей на оси координат:
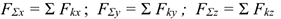
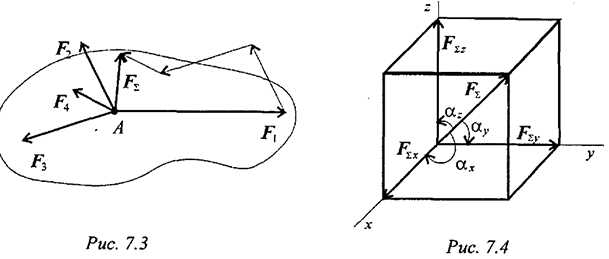
Модуль равнодействующей системы сходящихся сил определим по формул
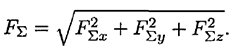
Направление вектора равнодействующей определяется углами
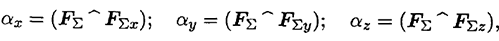
где
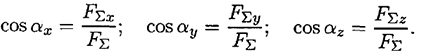
Произвольная пространственная система сил
Приведение произвольной пространственной системы сил к центру 
Дана пространственная система сил (рис. 7.5а). Приведем ее к центру 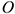 .
.
Силы необходимо параллельно перемещать, при этом образуется система пар сил. Момент каждой из этих пар равен произведению модуля силы на расстояние до центра приведения. В центре приведения возникает пучок сил, который может быть заменен суммарной силой (главный вектор) 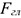 (рис. 7.56).
(рис. 7.56).
Моменты пар сил можно сложить, получив суммарный момент системы 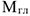 (главный момент). Таким образом, произвольная пространственная система сил приводится к главному вектору и главному моменту.
(главный момент). Таким образом, произвольная пространственная система сил приводится к главному вектору и главному моменту.
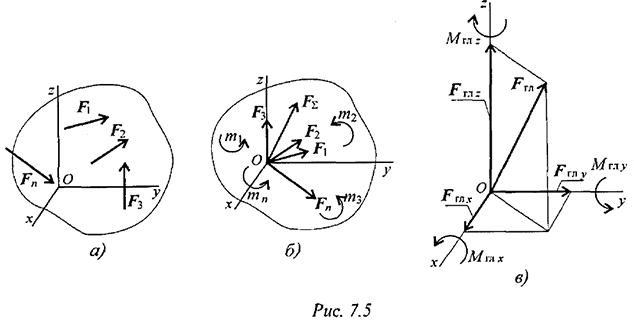
Главный вектор принято раскладывать на три составляющие, направленные вдоль осей координат (рис. 7.5в).
Обычно суммарный момент раскладывают на составляющие: три момента относительно осей координат.
Абсолютное значение главного вектора (рис. 7.56) равно
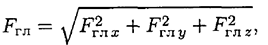
где
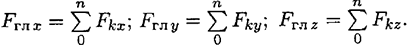
Абсолютное значение главного момента определяется по формуле
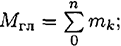
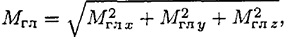
где
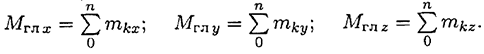
Уравнения равновесия пространственной системы
При равновесии 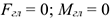 . Получаем шесть уравнений равновесия:
. Получаем шесть уравнений равновесия:
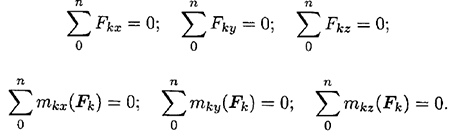
Шесть уравнений равновесия пространственной системы сил соответствуют шести независимым возможным перемещениям тела в пространстве: трем перемещениям вдоль координатных осей и трем вращениям вокруг этих осей.
Центр тяжести
Иметь представление о системе параллельных сил и центре системы параллельных сил, о силе тяжести и центре тяжести.’,
Знать методы для определения центра тяжести тела и формулы для определения положения центра тяжести плоских фигур.
Уметь определять положение центра тяжести простых геометрических фигур, составленных из стандартных профилей.
Сила тяжести
Сила тяжести — равнодействующая сил притяжения к Земле, она распределена по всему объему тела. Силы притяжения, приложенные к частицам твердого тела, образуют систему сил, линии действия которых сходятся в центре Земли (рис. 8.1). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
Точка приложения силы тяжести
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:
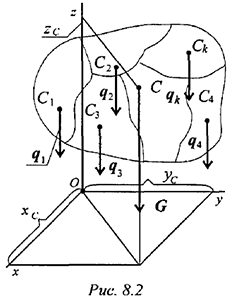
Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси. Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8.2).
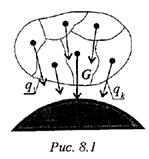
Тело состоит из частей, силы тяжести которых приложены в центрах тяжести (ЦТ) этих частей.Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре 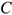 .
.
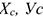 и
и 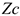 — координаты центра тяжести
— координаты центра тяжести 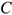 .
.
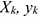 и
и 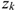 — координаты центров тяжести частей тела
— координаты центров тяжести частей тела
Из теоремы Вариньона следует:
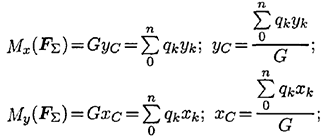
аналогично для оси 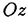 :
:
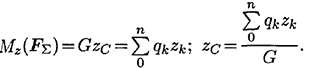
В однородном теле сила тяжести пропорциональна объему 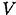 :
:
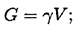
где 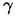 — вес единицы объема.
— вес единицы объема.
Следовательно, в формулах для однородных тел:
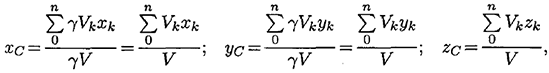
где 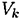 — объем элемента тела;
— объем элемента тела; 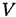 — объем всего тела.
— объем всего тела.
Центр тяжести однородных плоских тел (плоских фигур)
Очень часто приходится определять центр тяжести различных плоских тел и геометрических плоских фигур сложной формы. Для плоских тел можно записать: 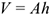 , где
, где 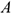 — площадь фигуры,
— площадь фигуры, 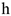 — ее высота.
— ее высота.
Тогда после подстановки в записанные выше формулы получим:
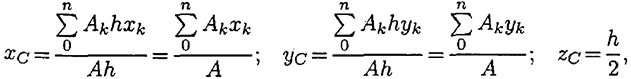
где 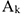 — площадь части сечения; сечения.
— площадь части сечения; сечения. 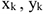 — координаты ЦТ частей Выражение
— координаты ЦТ частей Выражение 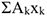 называют статическим моментом площади Координаты центра тяжести сечения можно выразить через статический момент:
называют статическим моментом площади Координаты центра тяжести сечения можно выразить через статический момент:
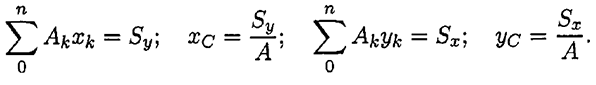
Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.
Определение координат центра тяжести плоских фигур
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине высоты. Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8.3: а) — круг; б) — квадрат, прямоугольник; в) — треугольник; г) — полукруг).
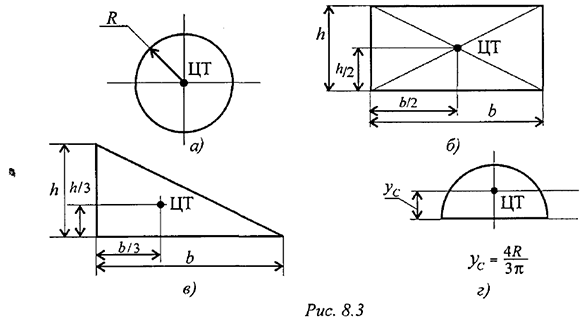
При решении задач используются следующие методы:
1) метод симметрии: центр тяжести симметричных фигур находится на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко определить;
3) метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.
Возможно эта страница вам будет полезна:
| Курсовая работа по технической механике |
Основные понятия кинематики. Кинематика точки
Иметь представление о пространстве, времени, траектории, пути, скорости и ускорении .Знать способы задания движения точки (естественный и координатный). Знать обозначения, единицы измерения, взаимосвязь кинематических параметров движения, формулы для определения скоростей и ускорений (без вывода).
Кинематика рассматривает движение как перемещение в пространстве. Причины, вызывающие движение, не рассматриваются. Кинематика устанавливает способы задания движения и определяет методы определения кинематических параметров движения.
Основные кинематические параметры
Траектория
Линию, которую очерчивает материальная точка при движении в пространстве, называют траекторией.
Траектория может быть прямой и кривой, плоской и пространственной линией. Уравнение траектории при плоском движении: 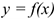 .
.
Пройденный путь
Путь измеряется вдоль траектории в направлении движения. Обозначение — 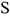 , единицы измерения — метры. Уравнение движения точки :
, единицы измерения — метры. Уравнение движения точки :
Уравнение, определяющее положение движущейся точки в зависимости от времени, называется уравнением движения.
Положение точки в каждый момент времени можно определить по расстоянию, пройденному вдоль траектории от некоторой неподвижной точки, рассматриваемой как начало отсчета. Такой способ задания движения называется естественным.
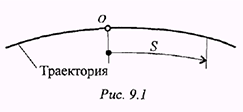
Таким образом, уравнение движения можно представить в виде 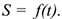
Положение точки можно также определить, если известны ее координаты в зависимости от времени (рис. 9.2). Тогда в случае движения на плоскости должны быть заданы два уравнения:
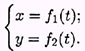
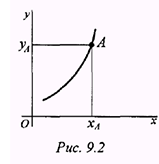
В случае пространственного движения добавляется и третья координата 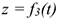 Такой способ задания движения называют координатным.
Такой способ задания движения называют координатным.
Скорость движения
Векторная величина, характеризующая в данный момент быстроту и направление движения по траектории, называется скоростью.
Скорость — вектор, в любой момент направленный по касательной к траектории в сторону направления движения (рис. 9.3).
Если точка за равные промежутки времени проходит равные расстояния, то движение называют равномерным.
Средняя скорость на пути 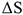 определяется как где
определяется как где 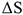 — пройденный путь за время
— пройденный путь за время 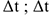 — промежуток времени.
— промежуток времени.
Если точка за равные промежутки времени проходит неравные пути, то движение называют неравномерным. В этом случае скорость — величина переменная и зависит от времени 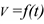 .
.
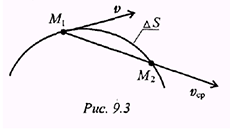
При рассмотрении малых промежутков времени 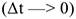 средняя скорость становится равной истинной скорости движения в данный момент. Поэтому скорость в данный момент определяют как производную пути по времени:
средняя скорость становится равной истинной скорости движения в данный момент. Поэтому скорость в данный момент определяют как производную пути по времени:
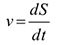
За единицу скорости принимают 1 м/с. Иногда скорость измеряют в км/ч,
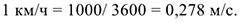
Ускорение точки
Векторная величина, характеризующая быстроту изменения скорости по величине и направлению, называется ускорением точки.
Скорость точки при перемещении из точки 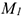 в точку
в точку 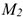 меняется по величине и направлению. Среднее значение ускорения этот промежуток времени
меняется по величине и направлению. Среднее значение ускорения этот промежуток времени
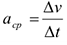
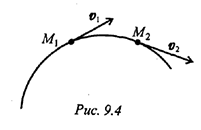
При рассмотрении бесконечно малого промежутка времени средне ускорение превратится в ускорение данный момент:
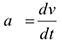
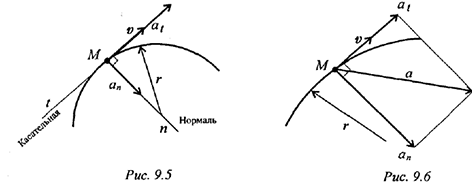
Обычно для удобства рассматривают две взаимно перпендикулярные составляющие ускорения: нормальное и касательно (рис. 9.5).
Нормальное ускорение 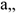 характеризует изменение скорости по направлению и определяется как
характеризует изменение скорости по направлению и определяется как 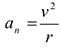 , где
, где 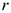 — радиус кривизны траектории в данный момент времени.
— радиус кривизны траектории в данный момент времени.
Нормальное ускорение всегда направлено перпендикулярно скорости к центру дуги. ; Касательное ускорение 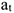 характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости, а при замедлении оно направлено противоположно направлению вектора скорости, формула для определения касательного ускорения имеет вид:
характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости, а при замедлении оно направлено противоположно направлению вектора скорости, формула для определения касательного ускорения имеет вид:
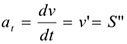
Значение полного ускорения определяется как
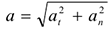
Кинематика точки
Иметь представление о скоростях средней и истинной, об ускорении при прямолинейном и криволинейном движениях, о различных видах движения точки.
Знать формулы (без вывода) и графики равномерного и равнопеременного движений точки. Уметь определять параметры движения точки по заданному закону движения, строить и читать кинематические графики.
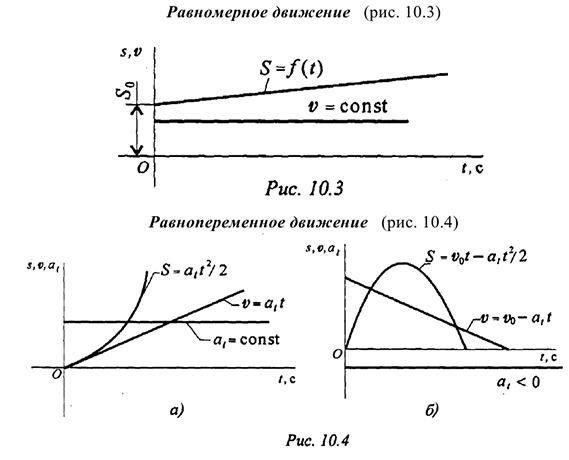
Анализ видов и кинетических параметров движений Равномерное движение
Равномерное движение — это движение с постоянной скоростью:
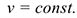
Для прямолинейного равномерного движения (рис. 10.1 а)
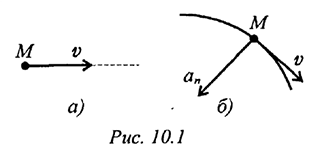
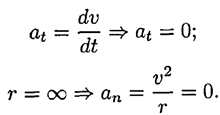
Полное ускорение движения точки равно нулю: 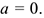 При криволинейном равномерном движении (рис. 10.16)
При криволинейном равномерном движении (рис. 10.16)
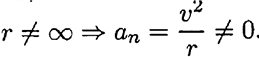
Полное ускорение равно нормальному ускорению: 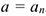 .
.
Уравнение (закон) движения точки при равномерном движении можно получить, проделав ряд несложных операций.
Так как 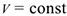 закон равномерного движения в общем виде является уравнением прямой:
закон равномерного движения в общем виде является уравнением прямой: 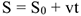 ,
,
где 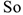 — путь, пройденный до начала отсчета.
— путь, пройденный до начала отсчета.
Равнопеременное движение
Равнопеременное движение — это движение с постоянным касательным ускорением:
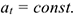
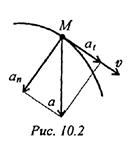
Для прямолинейного равнопеременного движения
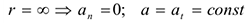
Полное ускорение равно касательному ускорению. Криволинейное равнопеременное движение (рис. 10.2):
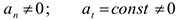
Учитывая, что:
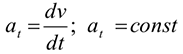
и сделав ряд преобразований:
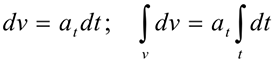
получим значение скорости при равнопеременном движении
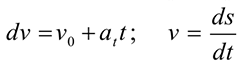
После интегрирования будем иметь закон равнопеременного движения в общем виде, представляющий уравнение параболы:
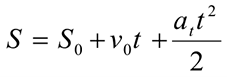
где 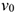 — начальная скорость движения;
— начальная скорость движения;
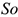 — путь, пройденный до начала отсчета;
— путь, пройденный до начала отсчета; 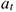 — постоянное касательное ускорение.
— постоянное касательное ускорение.
Неравномерное движение
При неравномерном движении численные значения скорости и ускорения меняются. Уравнение неравномерного движения в общем виде представляет собой уравнение третьей 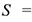
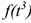 и выше степени.
и выше степени.
Кинематические графики
Кинематические графики — это графики изменения пути, скорости и ускорений в зависимости от времени.
Определение скорости и ускорения точки при координатном способе задании ее движении
Если движение точки задано в координатной форме, то каждое параметрическое уравнений , взятое отдельно, описывает движение не самой точки, а ее проекции вдоль соответствующих осей. Пусть движение точки 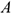 в плоской системе координат задано уравнениями
в плоской системе координат задано уравнениями
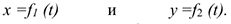
Первое из уравнений определяет закон изменения абсциссы 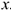 движущейся точки (рис. 1.118), т. е. описывает движение по оси абсцисс точки
движущейся точки (рис. 1.118), т. е. описывает движение по оси абсцисс точки 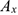 — проекции точки
— проекции точки 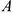 на ось
на ось 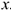 . Второе уравнение определяет закон изменения ординаты у точки
. Второе уравнение определяет закон изменения ординаты у точки 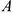 , т. е. описывает движение по оси ординат ее проекции
, т. е. описывает движение по оси ординат ее проекции 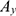 на эту ось. Допустим, что в данный момент времени
на эту ось. Допустим, что в данный момент времени 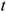 точка А имеет скорость
точка А имеет скорость 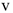 , тогда
, тогда 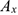 и
и 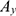 — проекции точки на оси
— проекции точки на оси 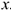 и
и 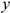 —движутся по осям со скоростями
—движутся по осям со скоростями 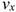 и
и 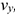 , модули которых равны проекциям скорости
, модули которых равны проекциям скорости 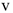 на соответствующие оси (рис. 10.5). Следовательно, дифференцируя каждое из заданных уравнений, найдем модули скоростей
на соответствующие оси (рис. 10.5). Следовательно, дифференцируя каждое из заданных уравнений, найдем модули скоростей 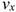 и
и 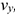 или, иначе говоря, проекции скорости
или, иначе говоря, проекции скорости 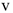 на оси координат. Итак,
на оси координат. Итак,
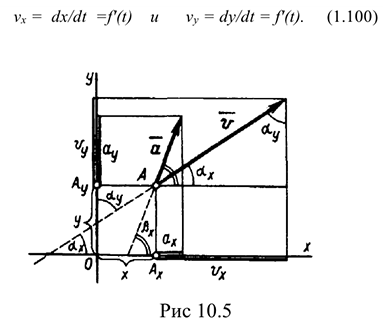
Если из начала и конца вектора 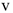 провести прямые, параллельные осям координат, то получим прямоугольный треугольник с гипотенузой к
провести прямые, параллельные осям координат, то получим прямоугольный треугольник с гипотенузой к 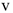 и катетами
и катетами 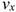 и
и 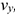 . Отсюда модуль искомой скорости
. Отсюда модуль искомой скорости
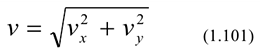
Направление скорости 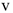 , т.е. углы
, т.е. углы 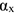 или
или 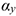 , находим по одной из следующих формул:
, находим по одной из следующих формул:
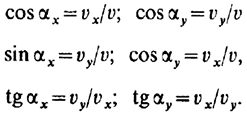
Аналогично определяется и вектор ускорения 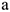 . Сначала находим его проекции на оси
. Сначала находим его проекции на оси 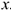 и
и 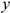 :
:
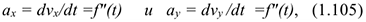
а затем модуль
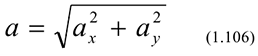
и направление, т. е. углы 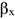 и
и 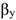 (угол
(угол 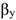 на рис. 1.118 не обозначен):
на рис. 1.118 не обозначен):
От координатного способа задания движения точки нетрудно перейти к естественному способу. Ранее мы рассмотрели , что, исключив время из уравнений движения 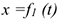 ,
, 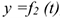 , получаем уравнение траектории
, получаем уравнение траектории 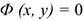 . Уравнение движения
. Уравнение движения 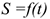 по этой траектории получаем следующим образом. Так как
по этой траектории получаем следующим образом. Так как 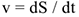 то
то 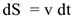 ; подставив сюда значение
; подставив сюда значение 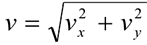 полученное из уравнений движения в осях координат, и проинтегрировав:
полученное из уравнений движения в осях координат, и проинтегрировав:
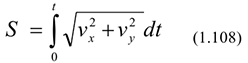
получим уравнения движения вида 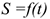 .
.
Например, если движение точки задано уравнениями 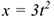 и
и 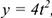 , то точка движется по прямолинейной траектории, уравнение которой
, то точка движется по прямолинейной траектории, уравнение которой 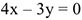 .
.
Из заданных уравнений движения следует, что проекции скорости на оси координат

а модуль скорости в любой момент времени
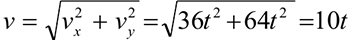
Из уравнения (1.108)
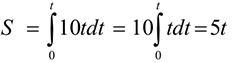
Таким образом, точка движется прямолинейно по траектории 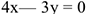 согласно уравнению
согласно уравнению 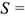
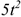 .
.
Возможно эта страница вам будет полезна:
| Контрольная работа по технической механике |
Простейшие движения твердого тела
Иметь представление о поступательном движении, его особенностях и параметрах, о вращательном движении тела и его параметрах. Знать формулы для определения параметров поступательного и вращательного движений тела.
Уметь определять кинематические параметры тела при поступательном и вращательном движениях, определять параметры любой точки тела.
Поступательное движение
Поступательным называют такое движение твердого тела, при котором всякая прямая линия на теле при движении остается параллельной своему начальному положению (рис. 11.1, 11.2). При поступательном движении всс точки тела движутся одинаково: скорости и ускорения в каждый момент одинаковы. Поэтому для описания движения тела можно рассматривать движение одной его точки, обычно центра масс.
Поступательное движение может быть прямолинейным и криволинейным.
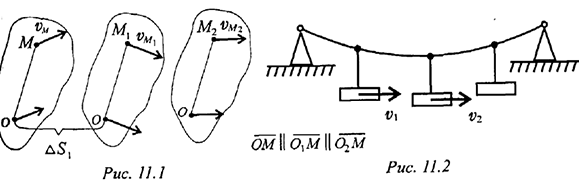
Вращательное движение
При вращательном движении все точки тела описывают окружности вокруг общей неподвижной
Неподвижная ось, вокруг которой вращаются все точки тела, называется осью вращения.
При этом каждая точка движется по окружности, радиус которой равен расстоянию точки до оси
вращения. Точки на оси вращения не перемещаются.
Для описания вращательного движения тела вокруг неподвижной оси можно использовать только угловые параметры (рис. 11.3): 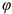 — угол поворота тела,
— угол поворота тела, 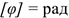 ;
;
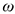 — угловая скорость, определяет изменение угла поворота в единицу времени,
— угловая скорость, определяет изменение угла поворота в единицу времени, 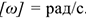 .
.
Для определения положения тела в любой момент времени используется уравнение 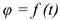
Следовательно, для определения угловой скорости можно пользоваться выражением 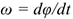
Иногда для оценки быстроты вращения используют угловую частоту вращения 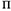 , которая оценивается в оборотах в минуту.
, которая оценивается в оборотах в минуту.
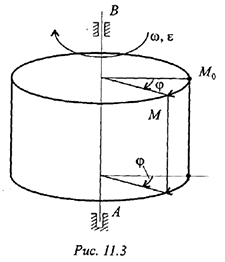
Угловая скорость и частота ; вращения физически близкие величины:
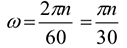
Изменение угловой скорости во времени определяется угловым ускорением 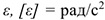 ;
;
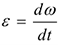
Частные случаи вращательного движения
Равномерное вращение (угловая скорость постоянна):
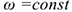
Уравнение (закон) равномерного вращения в данном случае имеет вид:

где 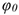 — угол поворота до начала отсчета.
— угол поворота до начала отсчета.
Кинематические графики для этого вида движения изображены на рис. 11.4.
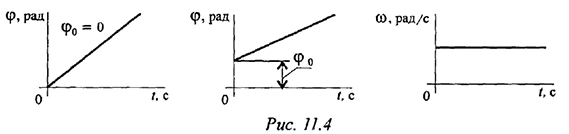
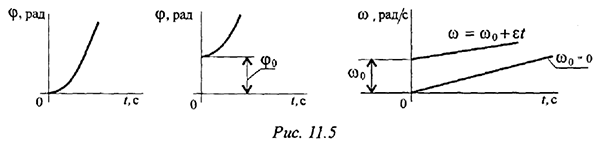
Равнопеременное вращение (угловое ускорение постоянно):
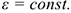
Уравнение (закон) равнопеременного вращения
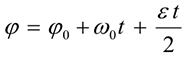
где 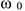 — начальная угловая скорость.
— начальная угловая скорость.
Угловое ускорение при ускоренном движении — величина положительная; угловая скорость будет все время возрастать.
Угловое ускорение при замедленном движении — величина отрицательная угловая скорость убывает.
Для данного движения кинематические графики представлены на рис. 11.5.
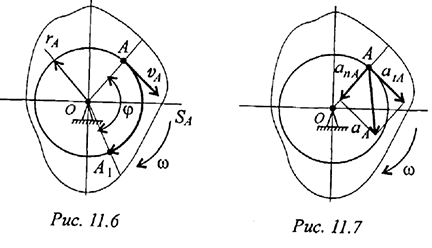
Скорости и ускорения точек вращающегося тела
Тело вращается вокруг точки 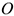 . Определим параметры движения точки
. Определим параметры движения точки 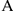 , расположенной на расстоянии
, расположенной на расстоянии 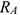 от оси вращения (рис. 11.6, 11.7). Путь точки
от оси вращения (рис. 11.6, 11.7). Путь точки 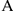 :
:
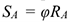
Линейная скорость точки 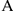 :
:
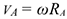
Ускорения точки 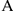 :
: 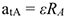 — касательное;
— касательное;
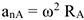 — нормальное, где
— нормальное, где 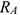 — радиус окружности, траектории точки
— радиус окружности, траектории точки 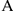 .
.
Примеры решения задач
Пример 1.
По заданному графику угловой скорости (рис. 11.8) определить вид вращательного движения.
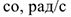
Решение
- Участок 1 — неравномерное ускоренное движение,
- Участок 2 — скорость постоянна — движение равномерное, .
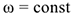
- Участок 3 — скорость убывает равномерно — равнозамедленное движение,
Сложное движение точки. Сложное движение твердого тела
Иметь представление о системах координат, об абсолютном, относительном и переносном движениях. Знать разложение сложного движения на относительное и переносное, теорему сложения скоростей. Знать разложение плоскопараллельного движения на поступательное и вращательное, способы определения мгновенного центра скоростей.
Основные определения
Сложным движением считают движение, которое можно разложить на несколько простых. Простыми движениями считают поступательное и вращательное.
Для рассмотрения сложного движения точки выбирают две системы отсчета: подвижную и неподвижную.
Движение точки (тела) относительно неподвижной системы отсчета называют сложным, или абсолютным.
Подвижную систему отсчета обычно связывают с движущимся телом. Движение подвижной системы отсчета относительно неподвижной называют переносным.
Движение материальной точки (тела) по отношению к подвижной системе называют относительным.
Примером может служить движение человека по эскалатору метро. Движение эскалатора — переносное движение, движение человека вниз или вверх по эскалатору — относительное, а движение по отношению к неподвижным стенам станции — сложное (абсолютное) движение. При решении задач используют теорему о сложении скоростей:
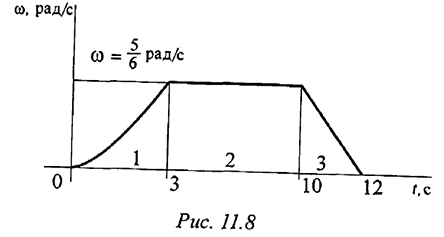
При сложном движении точки абсолютная скорость в каждый момент времени равна геометрической сумме переносной 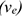 и относительной
и относительной 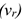 скоростей:
скоростей:
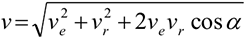
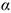 — угол между векторами
— угол между векторами 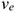 и
и 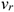 .
.
Плоскопараллельное движение твердого тела
Плоскопараллельным, или плоским, называется такое движение твердого тела, при котором все точки тела перемещаются параллельно некоторой неподвижной в рассматриваемой системе отсчета плоскости.
Плоскопараллельное движение можно изучать, рассматривая любое плоское сечение тела, параллельное неподвижной плоскости, называемой основной (рис. 12.1).
Все точки тела, расположенные на прямой, перпендикулярной к основной плоскости, движутся одинаково.
Плоскопараллельное движение изучается двумя методами: методом разложения сложного движения на поступательное и вращательное и методом мгновенных центров скоростей.
Метод разложения сложного движения на поступательное и вращательное
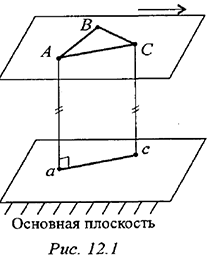
Плоскопараллельное движение раскладывают на два движения: поступательное вместе с некоторым полюсом и вращательное относительно этого полюса.
Разложение используют для определения скорости любой точки тела, применяя теорему о сложении скоростей (рис. 12.2).
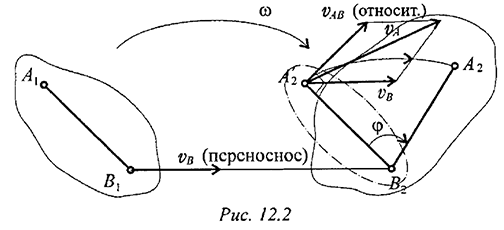
Точка 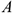 движется вместе с точкой
движется вместе с точкой 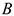 , а затем поворачивается вокруг
, а затем поворачивается вокруг 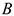 с угловой скоростью
с угловой скоростью 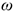 , тогда абсолютная скорость точки
, тогда абсолютная скорость точки 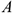 будет равна
будет равна
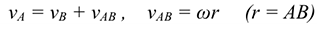
Примером плоскопараллельного движения может быть движение колеса на прямолинейном участке дороги (рис. 12.3). Скорость точки 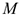
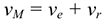
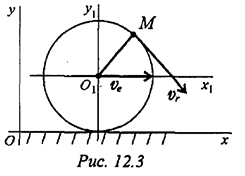
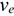 — скорость центра колеса переносная;
— скорость центра колеса переносная; 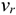 — скорость вокруг центра относительная.
— скорость вокруг центра относительная. 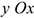 — неподвижная система координат,
— неподвижная система координат, 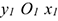 — подвижная система координат, связанная с осью колеса.
— подвижная система координат, связанная с осью колеса.
Метод определения мгновенного центра скоростей
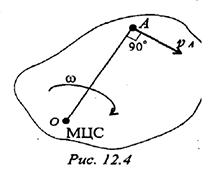
Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложное движение представляют в виде цепи вращений вокруг разных центров. Задача сводится к определению положения мгновенного центра 1 вращений (скоростей) (рис. 12.4).
Мгновенным центром скоростей (МЦС) является точка на плоскости, абсолютная скорость которой в данный момент равна нулю.
Вокруг этой точки тело совершает поворот со скоростью 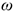 . Скорость точки
. Скорость точки 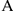 в данный момент равна
в данный момент равна
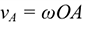
т.к. 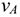 — линейная скорость точки
— линейная скорость точки 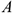 , вращающейся вокруг МЦС.
, вращающейся вокруг МЦС.
Существуют три способа определения положения мгновенного центра скоростей.
Первый способ. Известна скорость одной точки тела 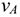 и угловая скорость вращения тела
и угловая скорость вращения тела 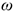 (рис. 12.5).
(рис. 12.5).
Точку 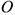 находим на перпендикуляре к вектору скорости
находим на перпендикуляре к вектору скорости 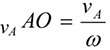 . Соединяем точку
. Соединяем точку 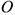 с точкой
с точкой 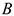 , замеряем расстояние
, замеряем расстояние 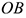
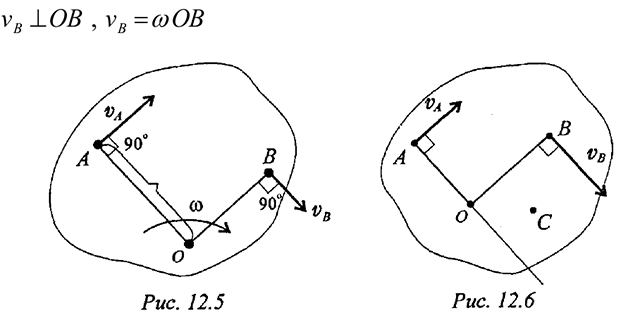
Второй способ. Известны скорости двух точек тела 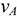 и
и 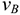 , и они не параллельны (рис. 12.6). Проводим из точек
, и они не параллельны (рис. 12.6). Проводим из точек 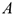 и
и 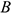 два перпендикуляра к известным векторам скоростей. На пересечении перпендикуляров находим МЦС. Далее можно найти скорость любой точки
два перпендикуляра к известным векторам скоростей. На пересечении перпендикуляров находим МЦС. Далее можно найти скорость любой точки 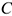 .
.
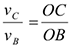
Третий способ. Известны скорости двух точек тела, и они параллельны 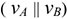 (рис. 12.7).
(рис. 12.7).
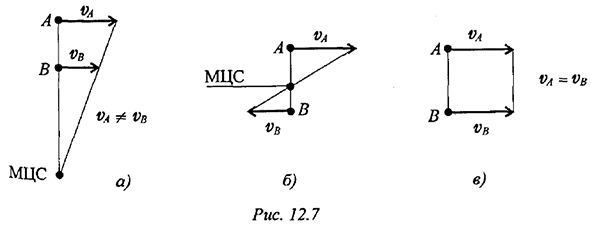
Соединяем концы векторов, МЦС находится на пересечении линии, соединяющей концы векторов с линией 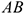 (рис. 12.7). При поступательном движении тела (рис. 12.7в) МЦС отсутствует.
(рис. 12.7). При поступательном движении тела (рис. 12.7в) МЦС отсутствует.
Возможно эта страница вам будет полезна:
| Заказать работу по технической механике |
Основные понятия и аксиомы динамики
Понятие о трении
Иметь представление о массе тела и ускорении свободного падения, о связи между силовыми и кинематическими параметрами движения, о двух основных задачах динамики. Знать аксиомы динамики и математическое выражение самого закона динамики. Знать зависимости для определения силы трения.
Содержание и задачи динамики
Динамика — раздел теоретической механики, в котором устанавливается связь между движением тел и действующими на них нами. В динамике решают два типа задач:
— определяют параметры движения по заданным силам;
— определяют силы, действующие на тело, по заданным кинематическим параметрам движения. При поступательном движении все точки тела движутся одинаково, поэтому тело можно принять за материальную точку. Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка падает с центром тяжести тела.
При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
Поэтому динамику делят на динамику точки и динамику материальной системы.
Аксиомы динамики
Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и четвертый законы были известны Галилею. Механику, основанную на этих законах, называют классической механикой.
Первая аксиома (принцип инерции)
Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния. Это состояние называют состоянием инерции. Вывести точку; из этого состояния, т.е. сообщить ей некоторое ускорение, может внешняя сила.
Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела.
Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы — килограмм (кг).
Вторая аксиома (второй закон Ньютона — основной закон динамики)
Зависимость между силой, действующей на материальную точку, и сообщаемым ею ускорением следующая:
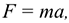
Где 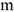 — масса точки, кг;
— масса точки, кг; 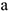 — ускорение точки,
— ускорение точки, 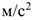 .
.
Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
Основной закон динамики в дифференциальной форме:
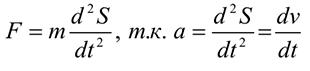
На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли:
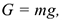
где 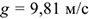 , ускорение свободного падения.
, ускорение свободного падения.
Третья аксиома (третий закон Ньютона)
Силы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны (рис. 13.1):
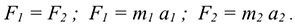
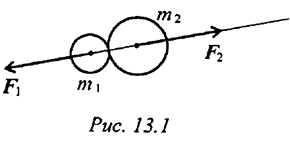
Откуда
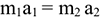
При взаимодействии ускорения обратно пропорциональны массам. Четвертая аксиома (закон независимости действия сил) Каждая сила системы сил действует так, как она действовала бы одна.
Ускорение, сообщаемое точке системой сил, равно геометрической сумме ускорений, сообщенных точке каждой силой в отдельности (рис. 13.2):
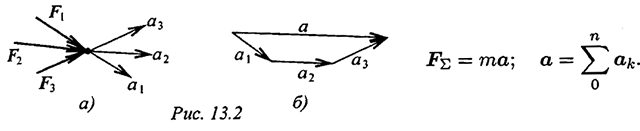
Понятие о трении. Виды трения
Трение — сопротивление, возникающее при движении одного шероховатого тела по поверхности другого. При скольжении тел возникает трение скольжения, при качении — трение качения. Природа сопротивлений движению в разных случаях различна. Трение скольжения
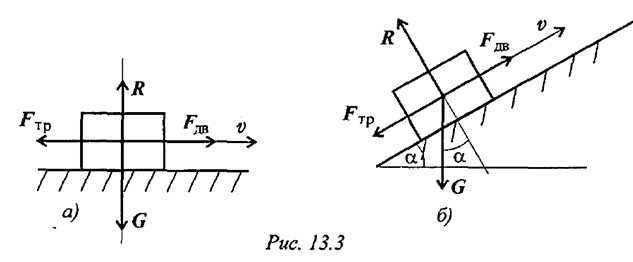
Причина — механическое зацепление выступов. Сила сопротивления движению при скольжении называется силой трения скольжения (рис. 13.3а).
Законы трения скольжения:
- Сила трения скольжения прямо пропорциональна силе нормального давления
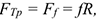
где 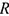 — сила нормального давления, направлена перпендикулярно опорной поверхности;
— сила нормального давления, направлена перпендикулярно опорной поверхности; 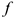 — коэффициент трения скольжения.
— коэффициент трения скольжения.
В случае движения тела по наклонной плоскости (рис. 13.36)
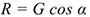
где 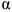 — угол наклона плоскости к горизонту.
— угол наклона плоскости к горизонту.
Сила трения всегда направлена в сторону, обратную направлению движения.
- Сила трения меняется от нуля до некоторого максимального значения, называемого силой трения покоя (статическое трение):
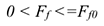
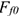 — статическая сила трения (сила трения покоя).
— статическая сила трения (сила трения покоя).
- Сила трения при движении меньше силы трения покоя Сила трения при движении называется динамической силой трения
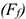
Поскольку сила нормального давления, зависящая от веса и направления опорной поверхности, не меняется, то различают статический и динамический коэффициенты трения:

Коэффициент трения скольжения зависит от следующих факторов:
— от материала: материалы делятся на фрикционные (с большим коэффициентом трения) и антифрикционные (с малым коэффициентом трения), например 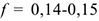 (при скольжении стали по стали всухую),
(при скольжении стали по стали всухую), 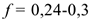 (при скольжении стали по текстолиту);— от наличия смазки, например
(при скольжении стали по текстолиту);— от наличия смазки, например 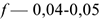 (при скольжении стали по стали со смазкой);
(при скольжении стали по стали со смазкой);
— от скорости взаимного перемещения.
Трение качения
Сопротивление при качении связано с взаимной деформацией грунта и колеса и значительно меньше трения скольжения.
Обычно считают грунт мягче колеса, тогда в основном деформируется грунт, и в каждый момент колесо должно перекатываться через выступ грунта. Для равномерного качения колеса необходимо прикладывать силу 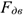 (рис. 13.4).
(рис. 13.4).
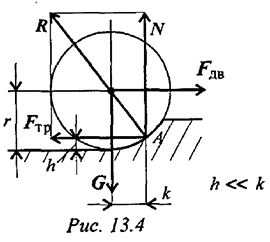
Условие качения колеса состоит в том, что движущийся момент должен быть не меньше момента сопротивления:
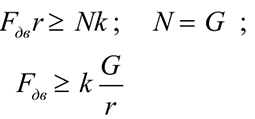
где  — максимальное значение плеча (половина колеи) принимается за коэффициент трения качения, размерность — сантиметры.
— максимальное значение плеча (половина колеи) принимается за коэффициент трения качения, размерность — сантиметры.
Ориентировочные значения  (определяются экспериментально):
(определяются экспериментально):
сталь по стали: 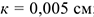 ;
;
резиновая шина по шоссе — 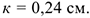
Возможно эта страница вам будет полезна:
| Яблонский решебник |
Движение материальной точки. Метод кинетостатики
Иметь представление о свободных и несвободных материальных точках, о силах инерции, об использовании силы инерции для решения технических задач. Знать формулы для расчета силы инерции при поступательном и вращательном движениях, знать принцип Даламбера и уметь определять параметры движения с использованием законов динамики и метода кинетостатики.
Свободная и несвободная точки
Материальная точка, движение которой в пространстве не ограничено какими-нибудь связями, называется свободной. Задачи решаются с помощью основного закона динамики.
Материальные точки, движение которых ограничено связями, называются несвободными. Для несвободных точек необходимо определять реакции связей. Эти точки движутся под действием активных сил и ограничивающих движение реакций связей (пассивных сил). Несвободные материальные точки освобождаются от связей: связи заменяются их реакциями. Далее несвободные точки можно рассматривать как свободные (принцип освобождасмости от связей).
Сила инерции
Инертность — способность сохранять свое состояние неизменным, это внутреннее свойство всех материальных тел.
Сила инерции — сила, возникающая при разгоне или торможении тела (материальной точки) и направленная в обратную сторону от ускорения. Силу инерции можно измерить, она приложена к «связям» — телам, связанным с разгоняющимся или тормозящимся телом. Рассчитано, что сила инерции равна
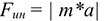
Таким образом, силы, действующие на материальные точки 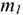 и
и 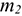 (рис. 14.1), при разгоне платформы соответственно равны
(рис. 14.1), при разгоне платформы соответственно равны
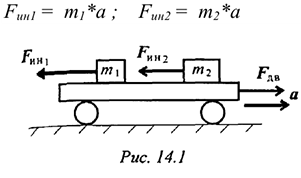
Разгоняющееся тело (платформа с массой 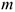 (рис. 14.1)) силу инерции не воспринимает, иначе разгон платформы вообще был бы невозможен. При вращательном движении (криволинейном) возникающее ускорение принято представлять в виде двух составляющих: нормального
(рис. 14.1)) силу инерции не воспринимает, иначе разгон платформы вообще был бы невозможен. При вращательном движении (криволинейном) возникающее ускорение принято представлять в виде двух составляющих: нормального 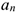 и касательного
и касательного 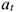 (рис. 14.2).
(рис. 14.2).
Поэтому при рассмотрении криволинейного движения могут возникнуть две составляющие силы инерции: нормальная и касательная
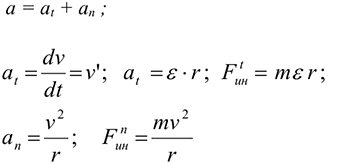
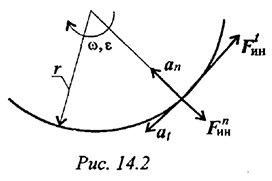
При равномерном движении по дуге всегда возникает нормальное ускорение, касательное ускорение равно нулю, поэтому действует только нормальная составляющая силы инерции, направленная по радиусу из центра дуги (рис. 14.3).

Принцип кинетостатики (принцип Даламбера)
Принцип кинетостатики используют для упрощения решения ряда технических задач. Реально силы инерции приложены к телам, связанным с разгоняющимся телом (к связям).
Даламбер предложил условно прикладывать силу инерции к активно разгоняющемуся телу. Тогда система сил, приложенных к материальной точке, становится уравновешенной, и можно при решении задач динамики использовать уравнения статики. Принцип Даламбера:
Материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равновесии;
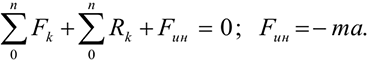
Порядок решения задач с использованием принципа Даламбера
- Составить расчетную схему.
- Выбрать систему координат.
- Выяснить направление и величину ускорения.
- Условно приложить силу инерции.
- Составить систему уравнений равновесия.
- Определить неизвестные величины.
Примеры решений задач
Пример 1.
Рассмотрим движение платформы по шероховатой поверхности с ускорением (рис. 14.4).
Решение
Активные силы: движущая сила, сила трения, сила тяжести. Реакция в опоре 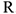 . Прикладываем силу инерции в обратную от ускорения сторону. По принципу Даламбера, система сил, действующих на платформу, становится уравновешенной, и можно составить уравнения равновесия. Наносим систему координат и составляем уравнения проекций сил.
. Прикладываем силу инерции в обратную от ускорения сторону. По принципу Даламбера, система сил, действующих на платформу, становится уравновешенной, и можно составить уравнения равновесия. Наносим систему координат и составляем уравнения проекций сил.
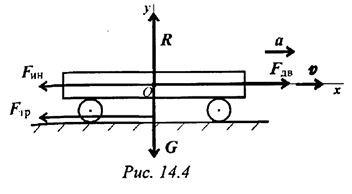
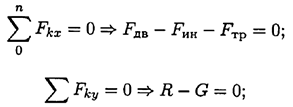
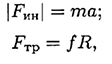
где 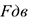 — движущая сила;
— движущая сила; 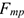 — сила трения;
— сила трения; 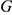 — сила тяжести;
— сила тяжести; 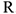 — реакция опоры;
— реакция опоры; 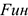 — сила инерции;
— сила инерции; 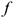 — коэффициент трения.
— коэффициент трения.
Пример 2.
Тело весом 3500 Н движется вверх по наклонной плоскости согласно уравнению 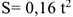 (рис. 14.5). Определить величину движущей силы, если коэффициент трения тела о плоскость
(рис. 14.5). Определить величину движущей силы, если коэффициент трения тела о плоскость 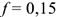 .
.
Решение
- Составим расчетную схему, выберем систему координат с осью
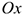 вдоль наклонной плоскости.
вдоль наклонной плоскости.
Активные силы: движущая, сила трения, сила тяжести. Наносим реакцию в опоре перпендикулярно плоскости. Чтобы верно направить силу инерции, необходимо знать направление ускорения, определить это можно по уравнению движения. При 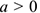 движение равноускоренное.
движение равноускоренное.
- Определяем ускорение движения:
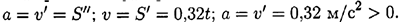
Силу 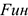 направим в обратную от ускорения сторону.
направим в обратную от ускорения сторону.
- По принципу Даламбера составим уравнения равновесия:
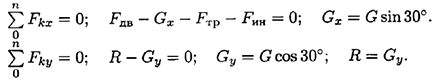
- Подставим все известные величины в уравнения равновесия:
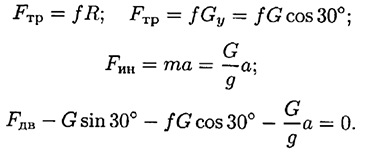
Выразим неизвестную силу и решим уравнение:
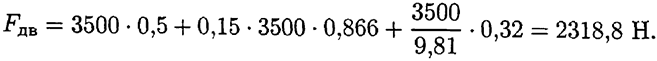
Работа и мощность
Иметь представление о работе силы при прямолинейном и криволинейном перемещениях, о jмощности полезной и затраченной, о коэффициенте полезного действия. Знать зависимости для определения силы трения, формулы для расчета работы и мощности при поступательном и вращательном движениях.
Уметь рассчитывать работу и мощность с учетом потерь на трение и сил инерции.
Работа
Для характеристики действия силы на некотором перемещении точки ее приложения вводят понятие «работа силы».
Работа служит мерой действия силы, работа — скалярная величина. Работа постоянной силы на прямолинейном пути
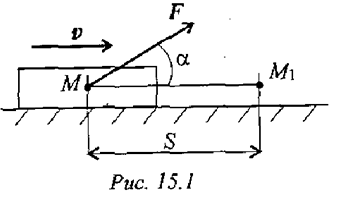
Работа силы в общем случае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения (рис. 15.1):
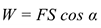
Единицы измерения работы:
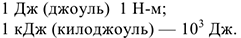
Рассмотрим частные случаи.
- Силы, совпадающие с направлением перемещения, называются движущими силами.
Направление вектора силы совпадает с направлением перемещения (рис. 15.2).
В этом случае 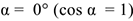 . Тогда
. Тогда 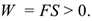
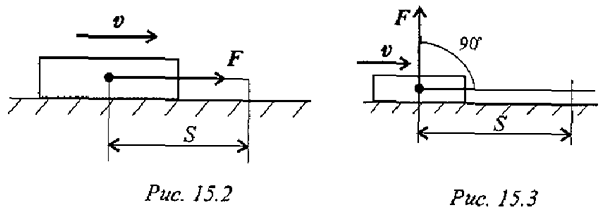
- Силы, перпендикулярные направлению перемещения, работы не производят (рис. 15.3). Сила
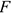 перпендикулярна направлению перемещения,
перпендикулярна направлению перемещения, 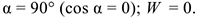 .
. - Силы, направленные в обратную от направления перемещения сторону, называются силами сопротивления (рис. 15.4).
Сила 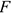 направлена в обратную от перемещения
направлена в обратную от перемещения 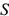 сторону. В этом случае
сторону. В этом случае 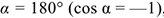 , следовательно,
, следовательно, 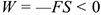 .
.
Движущие силы увеличивают модуль скорости, силы сопротивления уменьшают скорость.
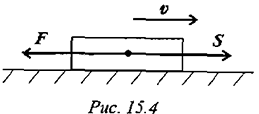
Таким образом, работа может быть положительной и отрицательной в зависимости от направления силы и скорости.
Работа постоянной силы на криволинейном пути
Пусть точка 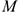 движется по дуге окружности и сила
движется по дуге окружности и сила 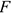 составляет некоторый угол а с касательной к окружности (рис. 15.5).
составляет некоторый угол а с касательной к окружности (рис. 15.5).
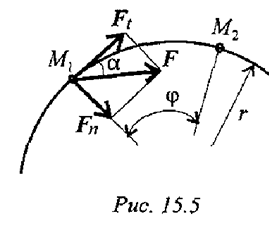
Вектор силы можно разложить на две составляющие
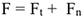
Используя принцип независимости действия сил, определим работу каждой из составляющих силы отдельно:
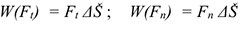
где 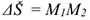 — пройденный путь,
— пройденный путь, 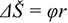 .
.
Нормальная составляющая силы 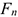 всегда направлена перпендикулярно перемещению и, следовательно, работы не производит:
всегда направлена перпендикулярно перемещению и, следовательно, работы не производит:
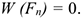
При перемещении по дуге обе составляющие силы разворачиваются вместе с точкой 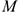 . Таким образом, касательная составляющая силы всегда совпадает по направлению с перемещением. Будем иметь:
. Таким образом, касательная составляющая силы всегда совпадает по направлению с перемещением. Будем иметь:
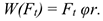
Касательную силу 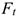 обычно называют окружной силой. Работа при криволинейном пути — это работа окружной силы:
обычно называют окружной силой. Работа при криволинейном пути — это работа окружной силы:
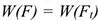
Произведение окружной силы на радиус называют вращающим моментом:
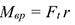
Работа силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угол поворота:
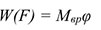
Работа силы тяжести
Работа силы тяжести зависит только от изменения высоты и равна произведению модуля силы тяжести на вертикальное перемещение точки (рис. 15.6):
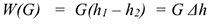
где 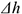 — изменение высоты. При опускании работа положительна, при подъеме отрицательна.
— изменение высоты. При опускании работа положительна, при подъеме отрицательна.
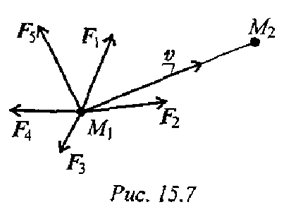
Работа равнодействующей силы
Под действием системы сил точка массой 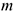 перемещается из положения
перемещается из положения 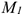 в положение
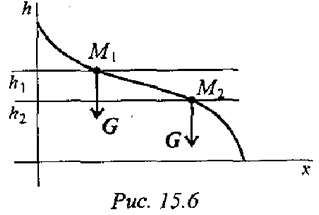
в положение 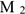 (рис. 15.7).
(рис. 15.7).
В случае движения под действием системы сил пользуются теоремой о работе равнодействующей.
Работа равнодействующей на некотором перемещении равна алгебраической сумме работ системы сил на том же перемещении
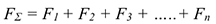
Работа равнодействующей силы
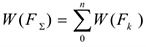
Примеры решения задач
Пример 1.
Тело массой 200 кг поднимают по наклонной илос кости (рис. 15.8).
Определите работу при перемещении на 10 см постоянной скоростью. Коэффициент трения тела о плоскость 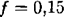 .
.
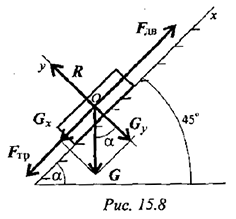
Решение
- При равномерном подъеме движущая сила равна сумме сил сопротивления движению. Наносим на схему силы, действующие на тело:
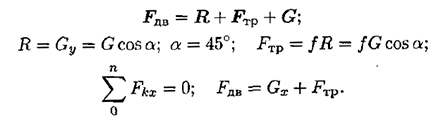
- Используем теорему о работе равнодействующей:
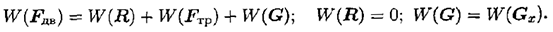
- Подставляем входящие величины и определяем работу по подъему:
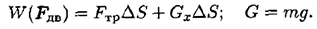
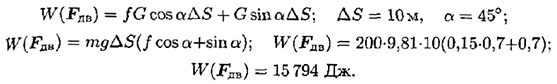
Пример 2.
Определите работу силы тяжести при перемещении груза из точки 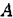 в точку
в точку 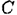 по наклонной плоскости (рис. 15.9). Сила тяжести тела 1500 Н.
по наклонной плоскости (рис. 15.9). Сила тяжести тела 1500 Н. 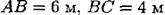 .
.
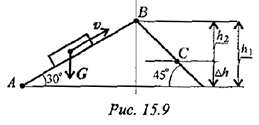
Решение
- Работа силы тяжести зависит только от изменения высоты груза. Изменение высоты при перемещении из точки
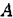 в
в 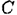 :
:
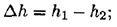
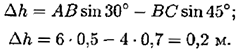
- Работа силы тяжести:
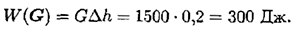
Работа и мощность. Коэффициент полезного действия
Иметь представление о мощности при прямолинейном и криволинейном перемещениях, о мощности полезной и затраченной, о коэффициенте полезного действия.
Знать зависимости для определения мощности при поступательном и вращательном движениях, КПД.
Уметь рассчитать мощность с учетом потерь на трение и сил инерции.
Мощность
Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.
Мощность — работа, выполненная в единицу времени:
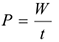
Единицы измерения мощности: ватты, киловатты. Мощность при поступательном движении (рис. 16.1)
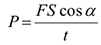
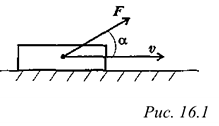
Учитывая, что 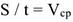 получи
получи
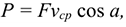
где 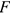 — модуль силы, действующей на тело;
— модуль силы, действующей на тело;
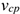 — средняя скорость движения тела. Средняя мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости.
— средняя скорость движения тела. Средняя мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости.
Мощность при вращении
Тело движется по дуге радиуса из точки 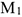 в точку
в точку 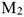
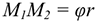
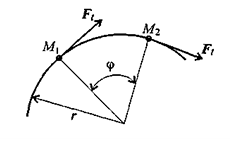
Работа силы
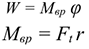
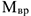 — вращающий момент
— вращающий момент
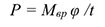
Учитывая, что, 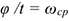 получим
получим
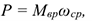
где 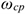 — средняя угловая скорость.
— средняя угловая скорость.
Мощность силы при вращении равна произведению вращающее го момента на среднюю угловую скорость.
Если при выполнении работы усилие машины и скорость движения меняются, можно определить мощность в любой момент времени, зная значения усилия и скорости в данный момент.
Коэффициент полезного действия
Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений.
Таким образом, машина (механизм) кроме полезной работы совершает еще и дополнительную работу.
Отношение полезной работы к полной работе или полезной мощности ко всей затраченной мощности называется коэффициентом полезного действия (КПД):

Полезная работа (мощность) расходуется на движение с заданной скоростью и определяется по формулам:
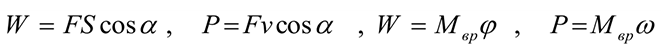
Затраченная мощность больше полезной на величину мощности, идущей на преодоление трения в звеньях машины, на утечки и тому подобные потери. Чем выше КПД, тем совершеннее машина.
Общие теоремы динамики
Иметь представление о понятиях «импульс силы», «количество движения», «кинетическая энергия», о системе материальных точек, о внутренних и внешних силах системы.
Знать основные теоремы динамики, основные уравнения динамики при поступательном и вращательном движениях твердого тела, формулы для расчета моментов инерции некоторых однородных твердых тел.
Уметь определять параметры движения с помощью теорем динамики.
Теорема об изменении количества движения
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость 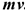 .
.
Вектор количества движения совпадает по направлению с вектором скорости. Единица измерения 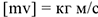 .
.
Произведение постоянного вектора силы на некоторый промежуток времени, в течение которого действует эта сила, называется импульсом силы 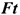 .
.
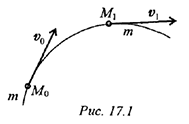
Вектор импульса силы по направлению совпадает с вектором силы. 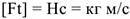 Использовав основное уравнение динамики, после преобразования можно получить соотношение между количеством движения и импульсом силы (рис. 17.1).
Использовав основное уравнение динамики, после преобразования можно получить соотношение между количеством движения и импульсом силы (рис. 17.1).
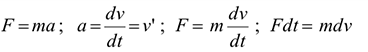
Проинтегрируем обе части равенства:
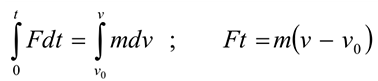
Полученное соотношение выражает теорему об изменении количества движения точки: Изменение количества движения точки за некоторый промежуток времени равно импульсу силы, действующему на точку в течение того же промежутка времени.
Теорема об изменении кинетической энергии
Энергией называется способность тела совершать механическую работу.
Существуют две формы механической энергии: потенциальная энергия, или энергия положения, и кинетическая энергия, или энергия движения.
Потенциальная энергия (П) определяет способность тела совершать работу при опускании с некоторой высоты до уровня моря. Потенциальная энергия численно равна работе силы тяжести.
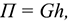
где 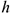 — высота точки над уровнем моря.
— высота точки над уровнем моря.
Кинетическая энергия 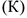 определяется способностью движущегося тела совершать работу. Для материальной точки кинетическая энергия рассчитывается по формуле
определяется способностью движущегося тела совершать работу. Для материальной точки кинетическая энергия рассчитывается по формуле
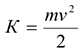
Кинетическая энергия — величина скалярная, положительная.
Единицы измерения:
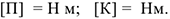
Энергия имеет размерность работы.
Запишем для материальной точки (рис. 17.2) основное уравнение движения
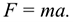
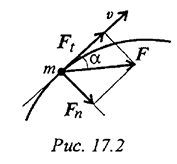
Спроектируем обе части векторного равенства на направление скорости:
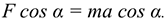
Известно, что
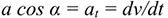
Откуда
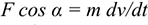
Умножив обе части полученного выражения на некоторое перемещение 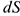 , получим:
, получим:
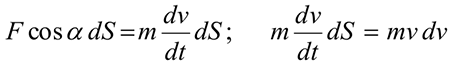
Интегрируем обе части равенства
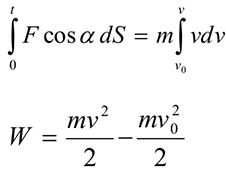
Полученное равенство выражает теорему об изменении кинетической энергии точки: Изменение кинетической энергии на некотором пути равно работе всех действующих на точку сил на том же пути.
Основы динамики системы материальных точек
Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой.
Любое материальное тело в механике рассматривается как механическая система, образуемая совокупностью материальных точек.
Из определения механической системы следует, что движение каждой из точек, входящих в систему, зависит от движения остальных точек.
Силы, действующие на точки системы, делятся на внешние и внутренние. Силы взаимодействия между точками этой системы называют внутренними.
К внешним силам относятся силы, действующие со стороны точек, не входящих в эту систему. Примерами внешних сил являются сила тяжести, сила давления, сила трения и др. К внутренним силам относятся силы упругости.
Движение механической системы зависит не только от внешних сил, но и от суммарной массы системы 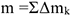
Где 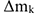 — масса отдельных точек механической системы.
— масса отдельных точек механической системы.
Движение системы зависит и от положения центра масс системы — условной точки, в которой сосредоточена вся масса тела. Обычно считают, что в центре масс приложены все внешние силы. Движение центра масс определяет движение всей системы только при поступательном движении, при котором все точки тела движутся одинаково.
Основное уравнение динамики при поступательном движении тела
Для определения движения тела (системы материальных точек) можно использовать второй закон динамики
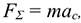
где 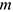 — суммарная масса тела;
— суммарная масса тела; 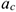 — ускорение центра масс тела. В поле земного притяжения центр масс совпадает с центром тяжести.
— ускорение центра масс тела. В поле земного притяжения центр масс совпадает с центром тяжести.
Основное уравнение динамики вращающегося тела
Пусть твердое тело под действием внешних сил вращается вокруг оси 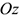 с угловой скоростью
с угловой скоростью  (рис. 17.3).
(рис. 17.3).
Рассматривая твердое тело как механическую систему, разобьем се на множество материальных точек с массами  . Каждая точка движется по окружности радиуса
. Каждая точка движется по окружности радиуса 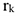
с касательным ускорением 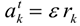
и нормальным ускорением 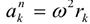
где 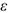 — угловое ускорение.
— угловое ускорение.
Используем для каждой точки принцип Даламбсра и приложим силы инерции:
— касательную 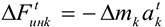
— нормальную 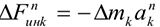
Система сил, действующих на точку, по принципу Даламбера, находится в равновесии.
Поэтому алгебраическая сумма моментов относительно оси вращения должна быть равна нулю:
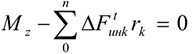
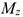 — момент внешних сил.
— момент внешних сил.
Моменты нормальных сил инерции 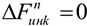 равны нулю, т. к. силы пересекают ось
равны нулю, т. к. силы пересекают ось 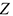 . Силы, направленные по касательной к окружности, равны
. Силы, направленные по касательной к окружности, равны
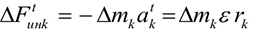
где 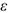 — общая величина, угловое ускорение тела.
— общая величина, угловое ускорение тела.
Подставив значение силы в формулу для определения моментов, получим
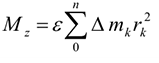
Величина 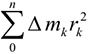 называется моментом инерции тела относительно оси вращения и обозначается
называется моментом инерции тела относительно оси вращения и обозначается 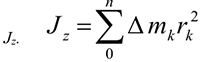
где 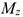 — сумма моментов внешних сил относительно оси;
— сумма моментов внешних сил относительно оси; 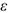 — угловое ускорение тела. Момент инерции тела в этом выражении определяет меру инертности тела при вращении. По выражению для момента инерции можно определить, что единица измерения этой величины в системе СИ
— угловое ускорение тела. Момент инерции тела в этом выражении определяет меру инертности тела при вращении. По выражению для момента инерции можно определить, что единица измерения этой величины в системе СИ 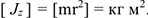 .
.
Видно, что значение момента инерции зависит от распределения массы относительно оси вращения: при одинаковой массе момент инерции больше, если основная часть массы расположена дальше от Оси вращения. Для увеличения момента инерции используют колеса Со спицами и отверстиями.
Моменты инерции некоторых тел
Момент инерции сплошного цилиндра (рис. 17.4)
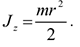
Момент инерции полого тонкостенного цилиндра (рис. 17.5)
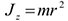
Момент инерции прямого тонкого стержня любого поперечного сечения
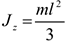
относительно  , рис. 17.6а
, рис. 17.6а
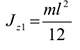
относительно  , рис. 17.6б
, рис. 17.6б
Момент инерции шара (рис. 17.7)
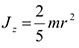

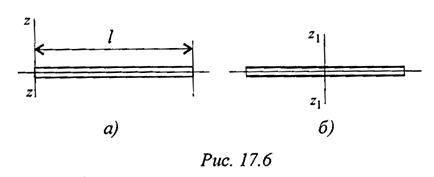
Основные положения. Нагрузки внешние и внутренние, метод сечений
Знать метод сечений, внутренние силовые факторы, составляющие напряжений.
Уметь определять виды нагружений и внутренние силовые факторы в поперечных сечениях.
Элементы конструкции при работе испытывают внешнее воздействие, которое оценивается величиной внешней силы. К внешним силам относят активные силы и реакции опор.
Под действием внешних сил в детали возникают внутренние силы упругости, стремящиеся вернуть телу первоначальную форму и размеры.
Внешние силы должны быть определены методами теоретической механики, а внутренние определяются основным методом сопротивления материалов — методом сечсний.
В сопротивлении материалов тела рассматриваются в равновесии. Для решения задач используют уравнения равновесия, полученные в теоретической механике для тела в пространстве.
Используется система координат, связанная с телом. Чаще продольную ось детали обозначают 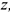 , начало координат совмещают с левым краем и размещают в центре тяжести сечения.
, начало координат совмещают с левым краем и размещают в центре тяжести сечения.
Метод сечений
Метод сечений заключается в мысленном рассечении тела плоскостью и рассмотрении равновесия любой из отсеченных частей.
Если всс тело находится в равновесии, то и каждая его часть находится в равновесии под действием внешних и внутренних сил.
Внутренние силы определяются из уравнений равновесия, составленных для рассматриваемой части тела.
Рассекаем тело поперек плоскостью (рис. 19.1). Рассматриваем правую часть. На нее действуют внешние силы 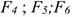 и внутренние силы упругости
и внутренние силы упругости 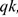 , распределенные по сечению. Систему распределенных сил можно заменить главным вектором
, распределенные по сечению. Систему распределенных сил можно заменить главным вектором  помешенным в центр тяжести сечения, и суммарным моментом сил
помешенным в центр тяжести сечения, и суммарным моментом сил 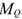 :
:
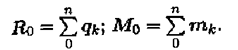
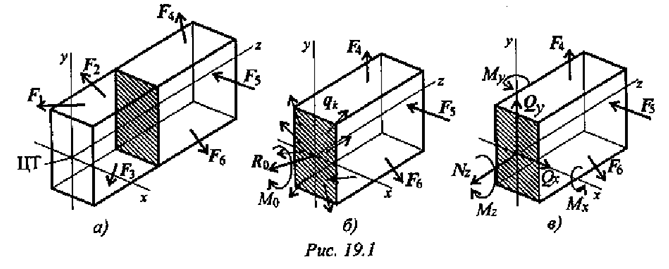
Разложив главный вектор 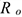 по осям получим три составляющие
по осям получим три составляющие
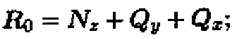
где 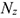 — продольная сила;
— продольная сила;
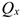 — поперечная сила по оси
— поперечная сила по оси 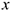
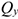 — поперечная сила по оси
— поперечная сила по оси 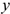 .
.
Главный момент тоже принято представлять в виде моментов пар сил в трех плоскостях проекции:
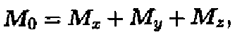
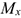 — момент сил относительно
— момент сил относительно 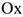 ;
;
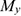 — момент сил относительно
— момент сил относительно 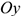
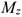 — момент сил относительно
— момент сил относительно 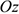 .
.
Полученные составляющие сил упругости носят название внутренних силовых факторов. Каждый из внутренних силовых факторов вызывает определенную деформацию детали. Внутренние силовые факторы уравновешивают приложенные к этому элементу детали внешние силы. Используя шесть уравнений равновесия, можно получить величину внутренних силовых факторов:
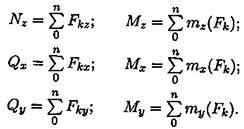
Из приведенных уравнений следует, что:
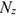 — продольная сила, равная алгебраической сумме проекций на ось
— продольная сила, равная алгебраической сумме проекций на ось 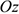 внешних сил, действующих на отсеченную часть бруса; вызывает растяжение или сжатие;
внешних сил, действующих на отсеченную часть бруса; вызывает растяжение или сжатие;
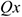 — поперечная сила, равная алгебраической сумме проекций на ось
— поперечная сила, равная алгебраической сумме проекций на ось 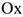 внешних сил, действующих на отсеченную часть;
внешних сил, действующих на отсеченную часть;
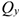 — поперечная сила, равная алгебраической сумме проекций на ось
— поперечная сила, равная алгебраической сумме проекций на ось 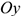 внешних сил, действующих на отсеченную часть;
внешних сил, действующих на отсеченную часть;
силы 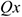 и
и 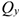 вызывают сдвиг сечения;
вызывают сдвиг сечения;
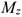 — крутящийся момент, равный алгебраической сумме моментов внешних сил относительно продольной оси
— крутящийся момент, равный алгебраической сумме моментов внешних сил относительно продольной оси 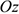 ; вызывает скручивание бруса;
; вызывает скручивание бруса;
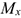 — изгибающий момент, равный алгебраической сумме моментов внешних сил относительно оси
— изгибающий момент, равный алгебраической сумме моментов внешних сил относительно оси 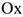 ;
;
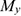 — изгибающий момент, равный алгебраической сумме моментов внешних сил относительно оси
— изгибающий момент, равный алгебраической сумме моментов внешних сил относительно оси 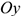 ;
;
моменты 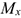 и
и 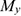 вызывают изгиб бруса в соответствующей плоскости.
вызывают изгиб бруса в соответствующей плоскости.
Напряжения
Метод сечений позволяет определить величину внутреннего силового фактора в сечении, но не дает возможности установить закон распределения внутренних сил по сечению. Для оценки прочности необходимо определить величину силы, приходящуюся на любую точку поперечного сечения.
Величину интенсивности внутренних сил в точке поперечного сечения называют механическим напряжением. Напряжение характеризует величину внутренней силы, приходящейся на единицу площади поперечного сечения.
Рассмотрим брус, к которому приложена внешняя нагрузка (рис. 19.2). С помощью метода сечений рассечем брус поперечной плоскостью, отбросим левую часть и рассмотрим равновесие оставшейся правой части. Выделим на секущей плоскости малую площадку 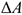 На этой площадке действует равнодействующая внутренних сил упругости.
На этой площадке действует равнодействующая внутренних сил упругости.
Направление напряжения 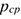 совпадает с направлением внутренней силы в этом сечении.
совпадает с направлением внутренней силы в этом сечении.
Вектор 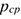 называют полным напряжением. Его принято раскладывать на два вектора (рис. 19.3):
называют полным напряжением. Его принято раскладывать на два вектора (рис. 19.3):
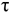 — лежащий в площадке сечения и
— лежащий в площадке сечения и
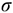 — направленный перпендикулярно площадке.
— направленный перпендикулярно площадке.
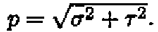
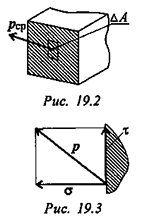
Если вектор 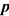 — пространственный, то его раскладывают на три составляющие:
— пространственный, то его раскладывают на три составляющие:
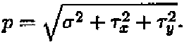
Нормальное напряжение характеризует сопротивление сечения растяжению или сжатию.
Касательное напряжение характеризует сопротивление сечения сдвигу.
Сила 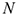 (продольная) вызывает появление нормального напряжения
(продольная) вызывает появление нормального напряжения 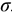 .
.
Силы 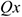 и
и 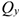 вызывают появление касательных напряжений
вызывают появление касательных напряжений 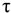 . Моменты изгибающие
. Моменты изгибающие 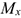 и
и 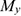 вызывают появление нормальных напряжений
вызывают появление нормальных напряжений 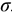 , переменных по сечению.
, переменных по сечению.
Крутящий момент 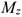 вызывает сдвиг сечения вокруг продольной оси, поэтому появляются касательные напряжения
вызывает сдвиг сечения вокруг продольной оси, поэтому появляются касательные напряжения 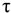 .
.
Растяжение и сжатие. Внутренние силовые факторы, напряжения. Построение эпюр
Иметь представление о продольных силах, о нормальных напряжениях в поперечных сечениях.
Знать правила построения эпюр продольных сил и нормальных напряжений, закон распределения нормальных напряжений в поперечном сечении бруса.
Уметь строить эпюры продольных сил и нормальных напряжений
Растяжение и сжатие
Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — продольная сила.
Продольные силы меняются по длине бруса. При расчетах после определения величин продольных сил по сечениям строится график — эпюра продольных сил.
Условно назначают знак продольной силы.
Если продольная сила направлена от положительной деформацией (рис. 20.1а).
Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией (рис. 20.16).
Примеры построения эпюры продольных сил
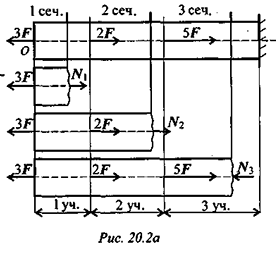
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а). Делим брус на участки нагружения.
Участком нагружения считают часть бруса между внешними силами. На представленном рисунке 3 участка нагружения.
Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
Участок 1:
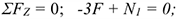
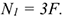
Продольная сила положительна, участок 1 — растянут.
Участок 2:
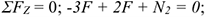
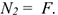
Продольная сила положительна, участок 2 — растянут.
Участок 3:
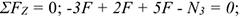

Продольная сила отрицательна, участок 3 — сжат. Полученное значение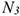 равно реакции в заделке.
равно реакции в заделке.
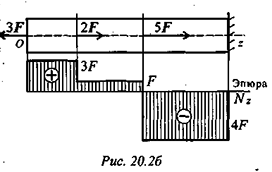
Под схемой бруса строим эпюру продольной силы (рис. 20.26).
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси. Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз. В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси 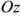 .
.
Правило контроля: в месте приложения внешней силы на эпюре должен быть скачок на величину приложенной силы.
На эпюре проставляются значения 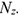 . Величины продольны: сил откладывают в заранее выбранном масштабе.
. Величины продольны: сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.
Изучая деформации при растяжении и сжатии, обнаруживаем что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.
Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси
Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечении равномерно.
Принцип смягчения граничных условий гласит: в точках тела удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.
Напряжения при растяжении и сжатии
При растяжении и сжатии в сечении действует только нормальное напряжение. Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис. 20.3).
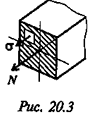
Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по формуле
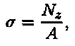
где 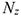 — продольная сила в сечении;
— продольная сила в сечении; 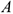 — площадь поперечного сечения. Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
— площадь поперечного сечения. Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
действуют при растяжении от сечения (рис. 20.4а), а при сжатии к сечению (рис. 20.46). Размерность (единица измерения)
напряжений — 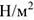 (Па), однако это слишком малая единица, и практически напряжения рассчитывают в
(Па), однако это слишком малая единица, и практически напряжения рассчитывают в 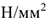 (МПа):
(МПа):
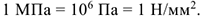
При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений.
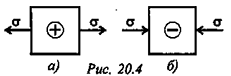
Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.
Строится и оформляется такая эпюра так же, как и эпюра продольных сил. Рассмотрим брус, нагруженный внешними силами вдоль оси (рис. 20.5). Обнаруживаем три участка нагружения и определяем величины продольных сил.
Участок 1:
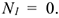
Внутренние продольные силы равны нулю.
Участок 2:
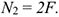
Продольная сила на участке положительна.
Участок 3:
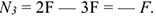
Продольная сила на участке отрицательна.
Брус —ступенчатый. С учетом изменений величин площади поперечного сечения участков напряжений больше.
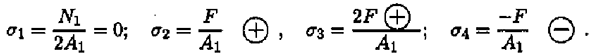
Строим эпюры продольных сил и нормальных напряжений.
Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.
Геометрические характеристики плоских сечений
Иметь представление о физическом смысле и порядке определения осевых, центробежных и полярных моментов инерции, о главных центральных осях и главных центральных моментах инерции.
Знать формулы моментов инерции простейших сечений, способы вычисления моментов инерции при параллельном переносе осей.
При растяжении, сжатии, смятии и сдвиге деталь сопротивляется деформации всем сечением одинаково. Здесь геометрической характеристикой сечения является площадь.
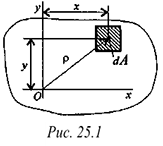
При кручении и изгибе сечение сопротивляется деформации не одинаково, при расчетах напряжений появляются другие геометрические характеристики сечения, влияющие на сопротивления сечения деформированию.
Статический момент площади сечения
Рассмотрим произвольное сечение (рис. 25.1).
Если разбить сечение на бесконечно малые площадки 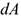 и умножить каждую площадку на расстояние до оси координат и проинтегрировать полученное выражение, получим статический момент площади сечения:
и умножить каждую площадку на расстояние до оси координат и проинтегрировать полученное выражение, получим статический момент площади сечения:
- 1) относительно оси
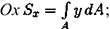
- 2) относительно оси
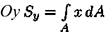
Для симметричного сечения статические моменты каждой половины площади равны по величине и имеют разный знак. Следовательно, статический момент относительно оси симметрии равен нулю.
Статический момент используется при определении положения центра тяжести сечения:
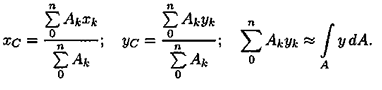
Формулы для определения положения центра тяжести можно зависать в виде
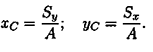
Центробежный момент инерции
Центробежным моментом инерции сечения называется взятая ко всей площади сумма произведений элементарных площадок на обе координаты:
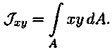
Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Центробежный момент инерции относительно осей, проходящих через центр тяжести сечения, равен кулю.
Оси, относительно которых центробежный момент равен нулю. Называются главными. Главные оси, проходящие через центр тяжести, называют главными центральными осями сечения.
Осевые моменты инерции
Осевым моментом инерции сечения относительно некоторой реи, лежащей в этой же плоскости, называется взятая по всей площади сумма произведений элементарных площадок на квадрат их расстояния до этой оси:
1) осевой момент инерции сечения относительно оси 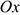
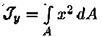
2) осевой момент инерции сечения относительно оси 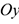
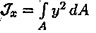
Полярный момент инерции сечения
Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей площади сумма произведений элементарных площадок на квадрат их расстояния до этой точки:
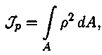
где 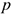 — расстояние до полюса (центра поворота) (рис. 25.1).
— расстояние до полюса (центра поворота) (рис. 25.1).
Поскольку 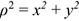 , получим: полярный момент инерции сечения равен сумме осевых:
, получим: полярный момент инерции сечения равен сумме осевых:
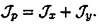
Осевые моменты инерции характеризуют сопротивление сечения повороту относительно соответствующей оси.
Полярный момент инерция характеризует сопротивление сечения повороту вокруг полюса (начала координат). Единицы измерения моментов инерции: 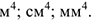
Моменты инерции простейших сечений
Осевые моменты инерции прямоугольника (рис. 25.2)
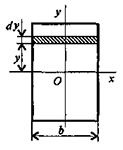
Представим прямоугольник высотой 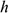 и шириной
и шириной 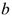 в виде сечения, составленного из бесконечно тонких полос. Запишем площадь такой полосы:,
в виде сечения, составленного из бесконечно тонких полос. Запишем площадь такой полосы:, 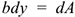 . Подставим в формулу осевого момента; инерции относительно оси
. Подставим в формулу осевого момента; инерции относительно оси 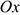 :
:
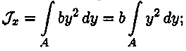
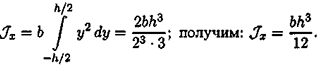
По аналогии, если разбить прямоугольник на вертикальные полосы, рассчитать площади полос и подставить в формулу для осевого момента инерции относительно оси 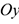 , получим
, получим
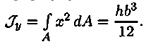
Очевидно, что при 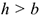 сопротивление повороту относительно оси
сопротивление повороту относительно оси 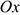 больше, чем относительно
больше, чем относительно 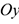 .
.
Для квадрата:
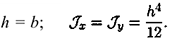
Полярный момент инерции круга
Для круга вначале вычисляют полярный момент инерции, затем — осевые. Представим круг в виде совокупности бесконечно тонких колец (рис. 25.3).
Площадь каждого кольца можно рассчитать как площадь прямоугольника с длинной стороной, равной длине соответствующей окружности, и высотой, равной толщине кольца:
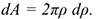
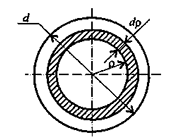
Подставим это выражение для площади в формулу для полярного момента инерции:
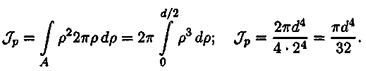
Получим формулу для расчета полярного момента инерции круга:
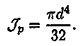
Подобным же образом можно получить формулу для расчета полярного момента инерции кольца:
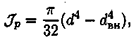
где 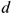 — наружный диаметр кольца;
— наружный диаметр кольца; 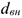 — внутренний диаметр кольца. Если обозначить
— внутренний диаметр кольца. Если обозначить 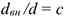 , то
, то
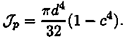
Кручение. Внутренние силовые факторы при кручении. Построение эпюр крутящих моментов
Иметь представление о деформациях при кручении, о внутренних силовых факторах при кручении. Уметь строить эпюры крутящих моментов.
Деформации при кручении
Кручение круглого бруса происходит при нагружении его парами сил с моментами в плоскостях, перпендикулярных продольной оси. При этом образующие бруса искривляются и разворачиваются на угол  , называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол
, называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол 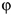 , называемый углом закручивания (угол поворота сечения, рис. 26.1). Длина бруса и размеры поперечного сечения при кручении не изменяются.
, называемый углом закручивания (угол поворота сечения, рис. 26.1). Длина бруса и размеры поперечного сечения при кручении не изменяются.
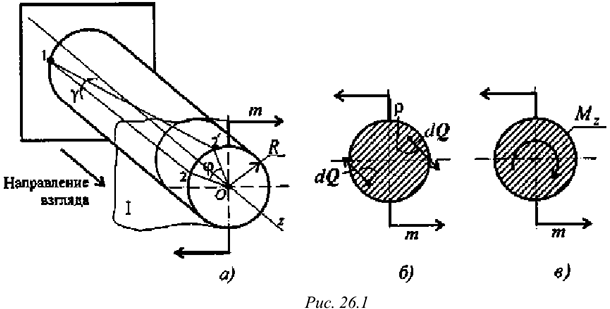
Связь между угловыми деформациями определяется соотношением
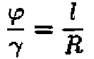
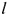 — длина бруса;
— длина бруса; 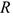 — радиус сечения.
— радиус сечения.
Длина бруса значительно больше радиуса сечения, следовательно, 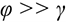 . Угловые деформации при кручении рассчитываются в радианах.
. Угловые деформации при кручении рассчитываются в радианах.
Гипотезы при кручении
- Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.
- Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).
- Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных селений не меняются.
Внутренние силовые факторы при кручении Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.
Внешними нагрузками также являются две противоположно направленные пары сил. Рассмотрим внутренние силовые факторы при кручении круглого бруса (рис. 26.1). Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 26.1а). Сечение рассматриваем со стороны Отброшенной части.
Внешний момент пары сил разворачивает участок бруса простив часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила 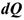 (рис. 26.16). Каждая точка сечения имеет симметричную, где возникает поперечная сила, направленная в обратную сторону. Эти силы Образуют пару с моментом
(рис. 26.16). Каждая точка сечения имеет симметричную, где возникает поперечная сила, направленная в обратную сторону. Эти силы Образуют пару с моментом 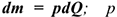 — расстояние от точки до центра сечения. Сумма поперечных сил в сечении равна нулю:
— расстояние от точки до центра сечения. Сумма поперечных сил в сечении равна нулю: 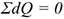 С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:
С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:
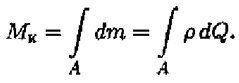
Практически крутящий момент определяется из условия равновесия отсеченной части бруса. Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26.1 в):
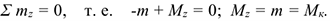
Эпюры крутящих моментов
Крутящие моменты могут меняться вдоль оси бруса. После определения величин моментов по сечениям строим график-эпюру крутящих моментов вдоль оси бруса.
Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае момент внутренних сил упругости направлен против часовой стрелки (рис. 26.2).Порядок построения эпюры моментов аналогичен построению эпюр продольных сил. Ось эпюры параллельна оси бруса, значения моментов откладывают от оси вверх или; вниз, масштаб построение выдерживать обязательно
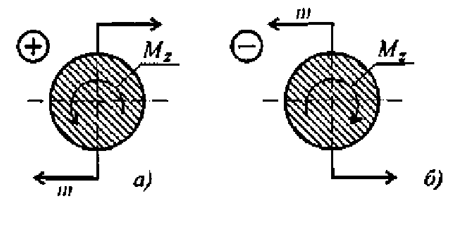
Кручение. Напряжения и деформации при кручении
Иметь представление о напряжении и деформациях при кручении, о моменте сопротивления при кручении.
Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении.
Напряжения при кручении
Проводим на поверхности бруса сетку из продольных и поперечных линий и рассмотрим рисунок, образовавшийся на поверхности после деформации (рис. 27.1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол 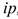 , продольные линии искривляются, прямоугольники превращаются в параллелограммы. Рассмотрим элемент бруса 1234 после деформации
, продольные линии искривляются, прямоугольники превращаются в параллелограммы. Рассмотрим элемент бруса 1234 после деформации
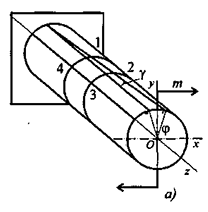
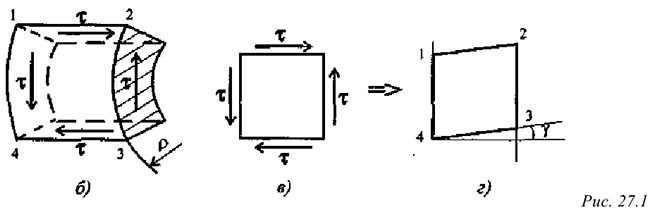
При выводе формул используем закон Гука при сдвиге и гипотезу плоских сечений и нсискривления радиусов поперечных ссчений.
При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27.16). При сдвиге на боковой поверхности элемента 1,2,3,4, возникают касательные напряжения, равные по величине (рис. 27.1 в), элемент деформируется (рис. 27.1 г).
Материал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига. Закон Гука при сдвиге 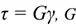 — модуль упругости при сдвиге,
— модуль упругости при сдвиге, 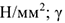 — угол сдвига, рад.
— угол сдвига, рад.
Напряжение в любой точке поперечного сечения
Рассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости 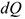 (рис. 27.2).
(рис. 27.2).
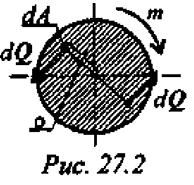
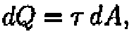
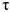 — касательное напряжение;
— касательное напряжение;
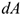 — элементарная площадка. В силу симметрии сечения силы
— элементарная площадка. В силу симметрии сечения силы 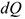 образуют пары (см. лекцию 26). Элементарный момент силы
образуют пары (см. лекцию 26). Элементарный момент силы 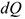 относительно центра круга
относительно центра круга
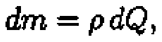
где 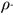 — расстояние от точки до центра круга.
— расстояние от точки до центра круга.
Суммарный момент сил упругости получаем сложением (интегрированием) элементарных моментов:
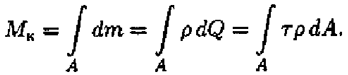
После преобразования получим формулу для определения напряжений в точке поперечного сечения:
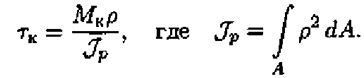
При 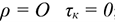 ; касательное напряжение при кручении пропорционально расстоянию от точки до центра сечения. Полученный интеграл
; касательное напряжение при кручении пропорционально расстоянию от точки до центра сечения. Полученный интеграл 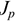 (лекция 25) называется полярным моментом инерции сечения.
(лекция 25) называется полярным моментом инерции сечения.  Является геометрической характеристикой сечения при кручении. Она характеризует сопротивление сечения скручиванию.
Является геометрической характеристикой сечения при кручении. Она характеризует сопротивление сечения скручиванию.
Анализ полученной формулы для  показывает, что слои, расположенные дальше от центра, испытывают большие напряжения.
показывает, что слои, расположенные дальше от центра, испытывают большие напряжения.
Эпюра распределения касательных напряжений при кручении (рис. 27.3)
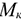 — крутящий момент в сечении;
— крутящий момент в сечении; 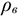 — расстояние от точки
— расстояние от точки 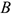 до центра;
до центра; 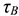 — напряжение в точке
— напряжение в точке 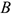 ;
; 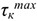 — максимальное напряжение.
— максимальное напряжение.
Максимальные напряжения при кручении
Из формулы для определения напряжений и эпюры распределения касательных напряжений при кручении видно, что максимальные напряжения возникают на поверхности.
Определим максимальное напряжение, учитывая, что 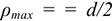 , где
, где 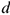 — диаметр бруса круглого сечения.
— диаметр бруса круглого сечения.
Для круглого сечения полярный момент инерции рассчитывается по формуле
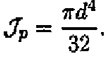
Максимальное напряжение возникает на поверхности, поэтому имеем
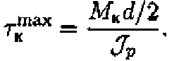
Обычно 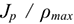 обозначают
обозначают 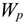 и называют моментом сопротивления при кручении, или полярным моментом сопротивления сечения
и называют моментом сопротивления при кручении, или полярным моментом сопротивления сечения
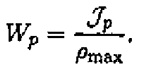
Таким образом, для расчета максимального напряжения на поверхности круглого бруса получаем формулу
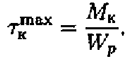
Для круглого сечения
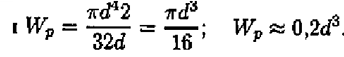
Для кольцевого сечения
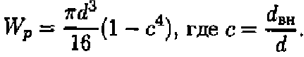
Условие прочности при кручении
Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности
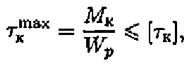
где 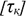 — допускаемое напряжение кручения.
— допускаемое напряжение кручения.
Виды расчетов на прочность
Существует два вида расчета на прочность
- Проектировочный расчет — определяется диаметр бруса (вала)в опасном сечении:
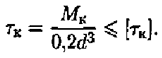
Откуда
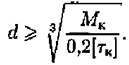
- Проверочный расчет — проверяется выполнение условия прочности
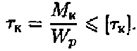
- Определение нагрузочной способности (максимального крутящего момента)
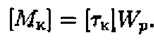
Расчет на жесткость
При расчете на жесткость определяется деформация и сравнивается с допускаемой. Рассмотрим деформацию круглого бруса над действием внешней пары сил с моментом 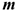 (рис. 27.4).
(рис. 27.4).
При кручении деформация оценивается углом закручивания:
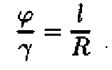
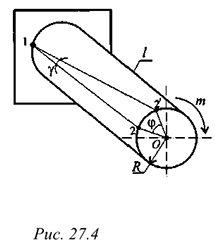
Здесь 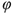 — угол закручивания;
— угол закручивания; 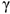 — угол сдвига;
— угол сдвига; 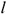 — длина бруса;
— длина бруса; 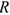 — радиус;
— радиус; 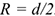 . Откуда
. Откуда
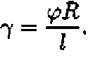
Закон Гука имеет вид 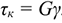 . Подставим выражение для
. Подставим выражение для 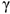 , получим
, получим
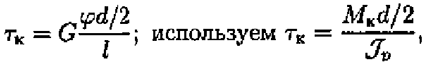
Откуда
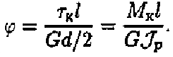
Произведение 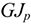 называют жесткостью сечения.
называют жесткостью сечения.
Модуль упругости можно определить как 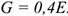 . Для стали
. Для стали 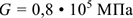 .
.
Обычно рассчитывается угол закручивания, приходящийся на один метр длины бруса (вала)  .
.
Условие жесткости при кручении можно записать в виде
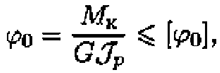
где  — относительный угол закручивания,
— относительный угол закручивания, 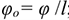 ;
;
 — допускаемый относительный угол закручивания.
— допускаемый относительный угол закручивания.
Изгиб. Классификация видов изгиба. Внутренние силовые факторы при изгибе
Иметь представление о видах изгиба и внутренних силовых факторах.
Знать методы для определения внутренних силовых факторов и уметь ими пользоваться для определения внутренних силовых факторов при прямом изгибе.
Основные определения
Изгибом называется такой вид нагружения, при котором в поперечном сечении бруса возникает внутренний силовой фактор —изгибающий момент. Брус , работающий на изгиб, называют балкой.
Изображен брус, закрепленный справа (за-щемление), нагруженный внешними силами и моментом (рис. 29.1). Плоскость, в которой расположены внешние силы и моменты, называют силовой плоскостью.Если все силы лежат в одной плоскости, изгиб называют плоским. Плоскость, проходящая через продольную ось бруса и одну из главных центральных осей его поперечного сечения, называется главной плоскостью бруса.
Если силовая плоскость совпадает с главной плоскостью бруса, изгиб называют прямым (рис. 29.1).
Если силовая плоскость не проходит через главную плоскость бруса, изгиб называют косым изгибом (рис. 29.2).
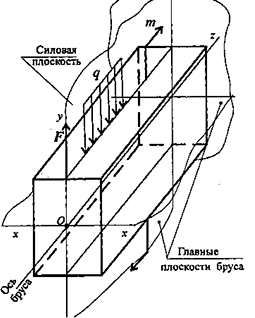
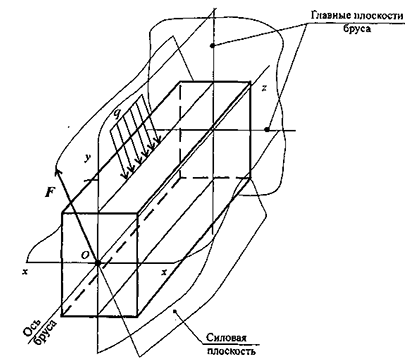
Внутренние силовые факторы при изгибе
Пример 1.
Рассмотрим балку, на которую действует пара сил с моментом  и внешняя сила
и внешняя сила 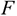 (рис. 29.3а). Для определения внутренних силовых факторов пользуемся методом сечений.
(рис. 29.3а). Для определения внутренних силовых факторов пользуемся методом сечений.
Рассмотрим равновесие участка 1 (рис. 29.36).
Под действием внешней пары сил участок стремится развернуться по часовой стрелке. Силы упругости, возникающие в сечении 1, удерживают участок в равновесии.
Продольные силы упругости выше оси бруса направлены направо, а силы ниже оси направлены налево. Таким образом, при равновесии участка 1 получим: 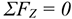 . Продольная сила
. Продольная сила 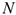 в сечении равна нулю. Момент сил упругости относительно оси
в сечении равна нулю. Момент сил упругости относительно оси 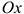 может быть получен, если суммировать элементарные моменты сил упругости в сечении 1-1 относительно оси
может быть получен, если суммировать элементарные моменты сил упругости в сечении 1-1 относительно оси 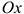
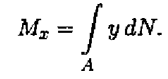
Этот момент называют изгибающим моментом  .
.
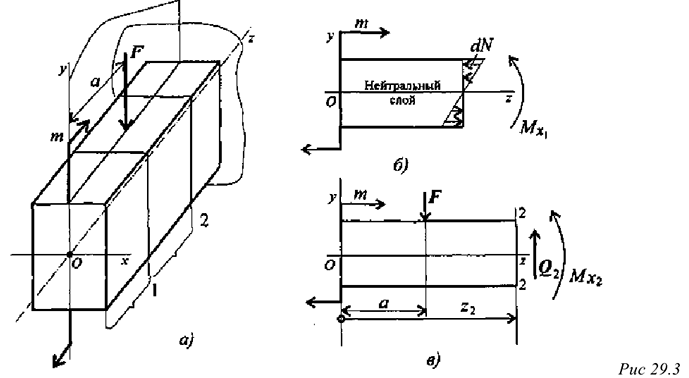
Из схемы вала на рис. 29.3 б видно, что часть волокон (выше оси) испытывают сжатие, а волокна ниже оси растянуты. Следовательно, в ссчснии должен существовать слой не растянутый и не сжатый, где напряжения а равны нулю.
Такой слой называют нейтральным слоем (НС). Линия пересечения нейтрального слоя с плоскостью поперечного сечения бруса называют нейтральной осью.
Нейтральный слой проходит через центр тяжести сечения. Здесь нейтральный слой совпадает с осью 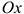 .
.
Практически величина изгибающего момента в сечении определяется из уравнения равновесия:
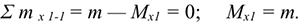
Таким образом, в сечении 1-1 продольная сила равна нулю, изгибающий момент в сечении постоянен.
Изгиб, при котором в поперечном сечении бруса возникает только изгибающий момент, называется чистым изгибом.
Рассмотрим равновесие участка бруса от свободного конца до сечения 2 (рис. 29.Зв). Запишем уравнения равновесия для участка бруса:
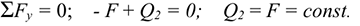
В сечении бруса 2-2 действует поперечная сила, вызывающая сдвиг.
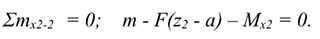
Изгибающий момент в сечении:
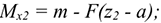
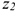 — расстояние от сечения 2 до начала координат.
— расстояние от сечения 2 до начала координат.
Изгибающий момент зависит от расстояния сечения до начала координат.
Изгиб, при котором в поперечном сечении бруса возникает изгибающий момент и поперечная сила, называется поперечным изгибом.
Принятые в машиностроении знаки поперечных сил и изгибающих моментов
Поперечная сила в сечении считается положительной, если она стремится развернуть сечение по часовой стрелке (рис. 29.4а), если против, — отрицательной (рис. 29.4б).
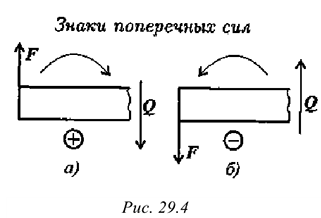
Знаки изгибающих моментов
Если действующие на участке внешние силы стремятся изогнуть балку выпуклостью вниз, то изгибающий момент считается положительным (рис. 29.5а), если наоборот — отрицательным (рис. 29.5 б).
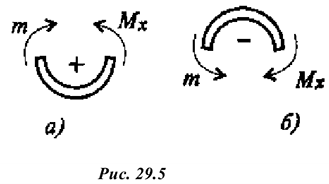
Выводы
При чистом изгибе в поперечном сечении балки возникает только изгибающий момент, постоянный по величине. При поперечном изгибе в сечении возникает изгибающий момент и поперечная сила.
Изгибающий момент в произвольном сечении балки численно равен алгебраической сумме моментов всех внешних сил, приложенных к отсеченной части, относительно рассматриваемого сечения. Поперечная сила в произвольном сечении балки численно равна алгебраической сумме проекций всех внешних сил, действующих на отсеченной части на соответствующую ось.
Пример 2.
На балку действует пара сил с моментом 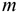 и распределенная нагрузка интенсивностью
и распределенная нагрузка интенсивностью  . Балка защемлена справа (рис. 29.6).
. Балка защемлена справа (рис. 29.6).
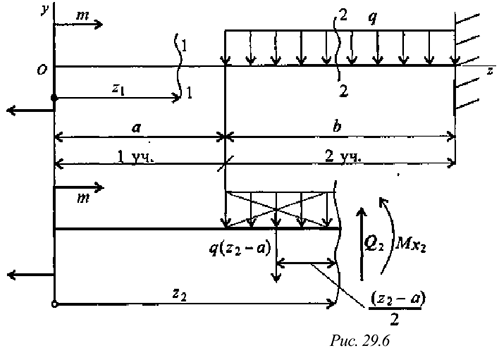
Рассечем балку на участке 1 на расстоянии 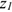 от левого края. Рассмотрим равновесие отсеченной части. Из уравнения
от левого края. Рассмотрим равновесие отсеченной части. Из уравнения 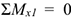 получим:
получим:
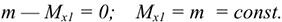
Участок 1 — участок чистого изгиба.
Рассечем балку на участке 2 на расстоянии 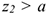 от края,
от края, 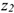 — расстояние сечения от начала координат.
— расстояние сечения от начала координат.
Из уравнения 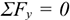 найдем поперечную силу
найдем поперечную силу 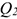 . Заменяем распределенную нагрузку на рассматриваемом участке равнодействующей силой
. Заменяем распределенную нагрузку на рассматриваемом участке равнодействующей силой 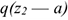 .
.
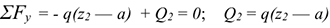
Из уравнения моментов определяем изгибающий момент в сечении:
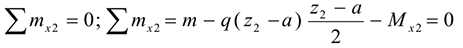
На втором участке возникает поперечный изгиб.
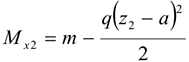
Выводы
При действии распределенной нагрузки возникает поперечная сила, линейно зависящая от координаты сечения.
Изгибающий момент на участке с распределенной нагрузкой меняется в зависимости от координаты сечения по параболическому закону.
Дифференциальные зависимости при прямом поперечном изгибе
Построение эпюр поперечных сил и изгибающих моментов существенно упрощается при использовании дифференциальных зависимостей между изгибающим моментом, поперечной силой и интенсивностью равномерно распределенной нагрузки (теорема Журав-ского):
Поперечная сила равна производной от изгибающего момента по длине балки:
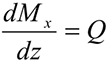
Интенсивность «равномерно распределенной нагрузки равна производной от поперечной силы по длине балки:
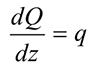
Из выше указанного следует:
если
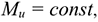
то
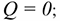
если
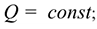
то
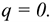
Кратко напомним, что при растяжении или сжатии возникает внутренний силовой фактор — продольная сила, при сдвиге — поперечная сила, а при кручении — крутящий момент в плоскости поперечного сечения.
Изгиб отличается от рассмотренных видов нагружения тем, что в этом случае появляются два внутренних силовых фактора: поперечная сила 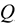 , как при сдвиге, и изгибающий момент
, как при сдвиге, и изгибающий момент  (рис. 101). Рассмотрим изгиб, при котором плоскость изгибающей нагрузки совпадает с одной из главных осей инерции
(рис. 101). Рассмотрим изгиб, при котором плоскость изгибающей нагрузки совпадает с одной из главных осей инерции
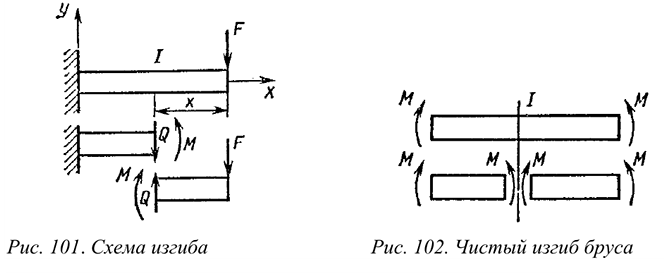
поперечного сечения. Такой изгиб иногда называется прямым, а чаще просто изгибом. Стержень, работающий на изгиб, называется балкой.
Частный вид изгиба, при котором поперечная сила равна нулю, называется чистым изгибом (рис. 102). В этом случае в поперечных сечениях балки возникает только изгибающий момент  . В отличие от него изгиб, при котором поперечная сила не равна нулю, называется поперечным изгибом (см. рис. 101).
. В отличие от него изгиб, при котором поперечная сила не равна нулю, называется поперечным изгибом (см. рис. 101).
Изгиб относится к простому виду нагружения, несмотря на то, что при изгибе балки возникают два внутренних силовых фактора  и
и 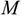 .
.
Однако, как покажет дальнейшее рассмотрение изгиба, определяющим внутренним силовым фактором при изгибе является единственный внутренний силовой, фактор — изгибающий момент. Влиянием перерезывающей силы при изгибе балки можно пренебречь.
Внутренние силовые факторы при изгибе 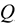 и
и 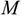 определяются методом сечений (см. рис. 101). Рассмотрим условия равновесия отсеченной части балки. Проекция всех сил на ось у равна нулю:
определяются методом сечений (см. рис. 101). Рассмотрим условия равновесия отсеченной части балки. Проекция всех сил на ось у равна нулю:
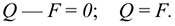
Момент относительно сечения 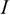 всех сил равен нулю
всех сил равен нулю
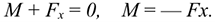
Поперечная сила 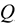 в сечении
в сечении 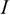 равна действующей на отсеченную часть внешней силе
равна действующей на отсеченную часть внешней силе 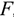 , а изгибающий момент
, а изгибающий момент 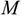 равен моменту внешней силы относительно рассматриваемого сечения.
равен моменту внешней силы относительно рассматриваемого сечения.
Теперь рассмотрим действие нескольких внешних сил на балку (рис. 103). В дальнейшем будем изображать балку в виде прямой линии — геометрического места центров тяжести поперечных сечений балки. Определим внутренние силовые факторы в произвольном сечении 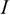 Для этого рассечем балку по сечению
Для этого рассечем балку по сечению 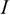 , приложим в этом сечении неизвестные внутренние силовые факторы при изгибе
, приложим в этом сечении неизвестные внутренние силовые факторы при изгибе 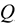 и
и 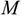 и составим уравнение равновесия для отсеченной части балки:
и составим уравнение равновесия для отсеченной части балки:

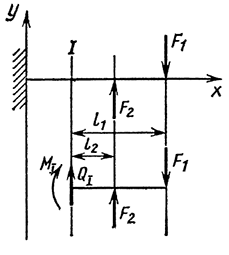
Сумма всех сил на ось 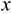 тождественно равна нулю, поскольку продольные силы на балку не действуют. В дальнейшем рассматриваем только два приведенных уравнения равновесия, индекс
тождественно равна нулю, поскольку продольные силы на балку не действуют. В дальнейшем рассматриваем только два приведенных уравнения равновесия, индекс  не указываем. Из первого уравнения следует
не указываем. Из первого уравнения следует
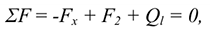
откуда определяем поперечную силу в сечении 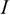 .
.
Определение внутренних силовых факторов при изгибе методов сечения.
Полученное выражение можно обобщить Поперечная сила в рассматриваемом сечении равна алгебраической сумме всех сил, действующих на балку до рассматриваемого сечения:
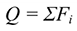
Поскольку речь идет об алгебраической сумме, в которой необходимо учитывать знак действующих сил, необходимо сформулировать правило знаков при определении значений поперечной силы в сечении; внешние силы активные и реактивные, лежащие по левую сторону от сечения, считаются положительными, если они направлены вверх, отрицательными — вниз, а по правую сторону — наоборот (рис. 104).
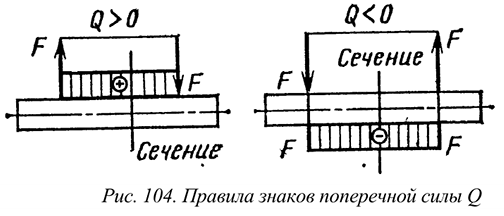
Перейдем к рассмотрению второго уравнения равновесия. Определим сумму моментов относительно рассматриваемого сечения 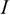
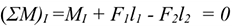
откуда
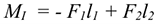
Это выражение также обобщим. Изгибающий момент в рассматриваемом сечении равен алгебраической сумме моментов относительно этого сечения всех внешних сил и моментов, действующих на балку до рассматриваемого сечения:
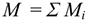
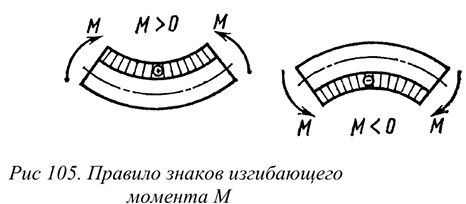
Сформулируем правило знаков при определении значения изгибающего момента: момент, изгибающий балку выпуклостью вниз, считается положительным, а вверх — отрицательным (рис. 105). Для лучшего запоминания правила знаков изгибающего момента следует отметить, что его значение откладывается в сторону сжатого волокна (см. рис. 105): при изгибе выпуклостью вниз сжатое волокно наверху балки, т. е. в плюс, а при изгибе выпуклостью вверх, сжатое волокно внизу — момент откладывается вниз — минус. Напомним, что существует три вида опор балок:
- 1) шарнирно-подвижная опора (рис. 106);
- 2) шарнирно-неподвижная опора (рис. 107);
- 3) жесткая заделка или защемление (рис. 108).
В опорах возникают силовые факторы, называемые реакциями опор. Два первых вида шарнирных опор допускают свободное проворачивание балки, и поэтому в них не возникает опорных моментов. Только жесткая заделка, не допускающая поворота балки в опоре, создает реактивный опорный момент.
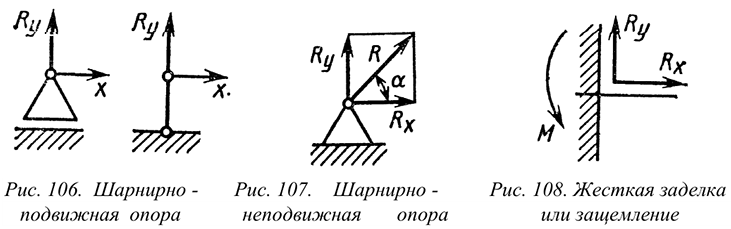
Подвижная шарнирная опора допускает свободное осевое перемещение балки на катках, поэтому в ней возникает только одна опорная реакция.
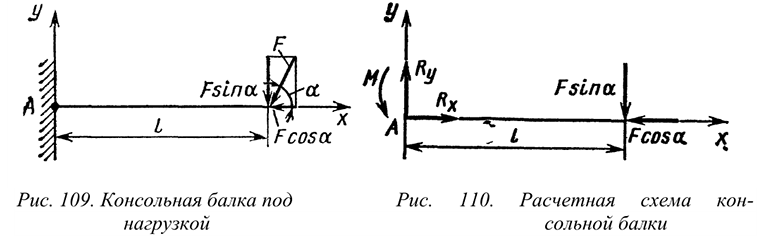
В неподвижной шарнирной опоре возникает реакция под углом а к горизонтальной оси, эта реакция может быть разложена на две реакции в горизонтальном и вертикальном направлениях. Угол 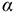 определяет отношение величин горизонтальной и вертикальной составляющих реакций опор:
определяет отношение величин горизонтальной и вертикальной составляющих реакций опор:
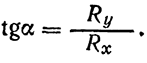
Жесткая заделка, или защемление, дает три реакции: 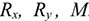 .
.
Рассмотрим, например, балку, нагруженную силой 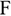 , защемленную с одной стороны, и свободную с другой (рис. 109). Такую балку называют консольной. Ось у направим вертикально, а ось
, защемленную с одной стороны, и свободную с другой (рис. 109). Такую балку называют консольной. Ось у направим вертикально, а ось 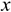 — горизонтально.
— горизонтально.
Действующую под углом 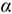 силу
силу 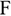 разложим по осям
разложим по осям 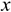 и
и 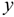 на
на 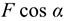 и
и 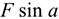 (см. рис. 109). В защемлении возникают три неизвестные реакции: две силы
(см. рис. 109). В защемлении возникают три неизвестные реакции: две силы 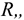 и
и 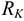 и момент
и момент 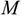 . Приложим к балке неизвестные опорные реакции и получим расчетную схему (рис. 110). Балка находится в равновесии, и поэтому должны быть справедливы три уравнения равновесия
. Приложим к балке неизвестные опорные реакции и получим расчетную схему (рис. 110). Балка находится в равновесии, и поэтому должны быть справедливы три уравнения равновесия
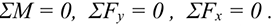
Подставим в эти уравнения силы и моменты, действующие на консоль:
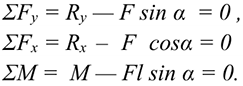
Момент взят относительно точки 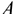 для простоты, чтобы исключить моменты неизвестных опорных реакций
для простоты, чтобы исключить моменты неизвестных опорных реакций 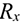 и
и 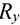 . Определим
. Определим
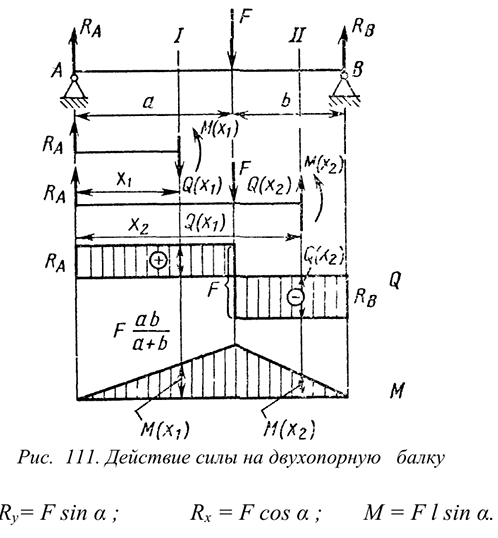
Из рассмотрения этого примера следует, что если действующие силы будут перпендикулярны оси балки, т. е. угол 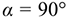 , то горизонтальных составляющих опорных реакций не будет:
, то горизонтальных составляющих опорных реакций не будет: 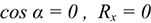 .
.
Теперь можно перейти к рассмотрению способов построения графиков изменения внутренних силовых факторов при изгибе 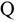 и
и 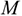 по длине балки или эпюр
по длине балки или эпюр 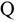 и
и 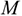 .
.
Предварительно рассмотрим несколько простейших примеров. Некоторые из них приведены в приложении III.
Пример 1.
Построить эпюры 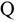 и
и 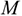 при изгибе балки на двух опорах или двухопорной балки под действием сосредоточенной силы
при изгибе балки на двух опорах или двухопорной балки под действием сосредоточенной силы 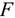 (рис. 111).
(рис. 111).
Решение. Определим опорные реакции 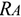 и
и 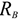 из уравнений равновесия балки
из уравнений равновесия балки
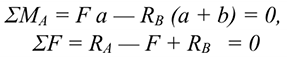
Из первого уравнения найдем 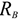
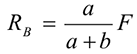
а из второго уравнения определим 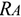
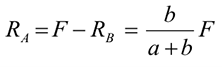
Разобьем балку на два участка и запишем выражение поперечных сил и изгибающих моментов для каждого из участков с учетом выведенных выше соотношений и принятых правил знаков:
для участка 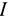 на расстоянии
на расстоянии 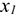 от опоры
от опоры 
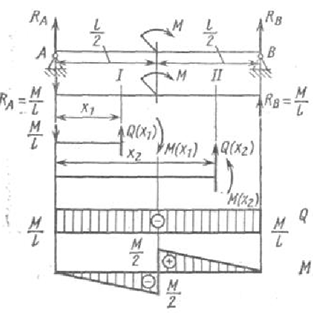
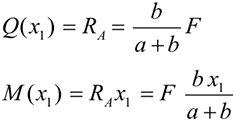
где
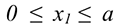
при
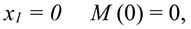
при
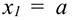
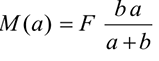
для участка II на расстоянии 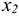 от опоры
от опоры 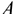
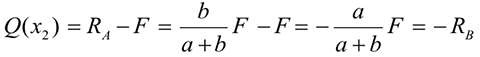
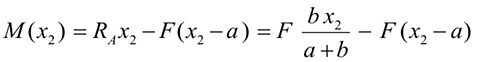
Где
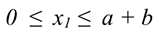
при
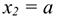
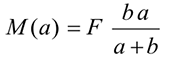
при

Таким образом, на каждом участке балки  постоянно, причем для участка I — положительно, а для II — отрицательно, а момент имеет линейную зависимость от
постоянно, причем для участка I — положительно, а для II — отрицательно, а момент имеет линейную зависимость от 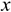 и на участке I возрастает от 0 до
и на участке I возрастает от 0 до 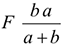 , а на участке II убывает от этой величины до нуля. С учетом этого построим эпюры
, а на участке II убывает от этой величины до нуля. С учетом этого построим эпюры 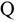 и
и 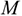 (см. рис. 111). Следует отметить, что там, где действует сила, на эпюре поперечных сил наблюдается скачок, равный по величине действующей силе. Так, на эпюре
(см. рис. 111). Следует отметить, что там, где действует сила, на эпюре поперечных сил наблюдается скачок, равный по величине действующей силе. Так, на эпюре 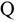 имеется три скачка там, где действуют силы
имеется три скачка там, где действуют силы 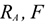 и
и  .
.
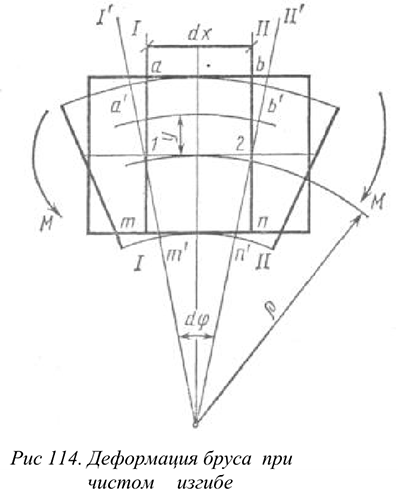
Если сила имеет знак плюс, скачок наблюдается вверх, если минус — вниз, в случае действия силы 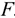 .
.
Определим связь между нормальным напряжением при изгибе балки а и изгибающим моментом 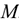 . Рассмотрим условия чистого изгиба балки (рис. 114), когда
. Рассмотрим условия чистого изгиба балки (рис. 114), когда 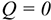 и в сечении действует только изгибающий момент. Опыт показывает, что соотношение для о при чистом изгибе можно использовать для определения нормальных напряжений при поперечном изгибе.
и в сечении действует только изгибающий момент. Опыт показывает, что соотношение для о при чистом изгибе можно использовать для определения нормальных напряжений при поперечном изгибе.
Рассмотрим положение двух плоскостей I , II , лежащих друг от друга на малом расстоянии 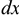 (см. рис. 114). При изгибе так же, как и при растяжении и кручении, справедлива гипотеза плоских сечений. Сечения I и II, плоские до изгиба, остались плоскими и после изгиба
(см. рис. 114). При изгибе так же, как и при растяжении и кручении, справедлива гипотеза плоских сечений. Сечения I и II, плоские до изгиба, остались плоскими и после изгиба 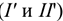 . Только при этом повернулись на некоторый малый угол
. Только при этом повернулись на некоторый малый угол 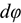 , оставаясь перпендикулярными к наружным поверхностям балки. При этом верхние волокна балки растянулись, их длина
, оставаясь перпендикулярными к наружным поверхностям балки. При этом верхние волокна балки растянулись, их длина 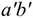 стала больше прежней
стала больше прежней 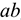 , а нижние волокна балки
, а нижние волокна балки 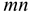 сжались и приняли положение
сжались и приняли положение 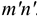 .
.
Логично предположить, что между верхними и нижними волокнами имеется линия раздела 1—2, называемая нейтральным слоем, который при изгибе не будет менять своей длины. При чистом изгибе он примет форму дуги окружности радиуса 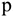 . Рассмотрим деформацию произвольного волокна
. Рассмотрим деформацию произвольного волокна 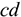 балки на расстоянии
балки на расстоянии 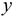 от нейтрального слоя 1—2 (рис. 115). Проведем из точки 2 прямую
от нейтрального слоя 1—2 (рис. 115). Проведем из точки 2 прямую 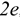 , параллельную
, параллельную 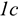 , тогда
, тогда 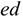 будет равна удлинению волокна
будет равна удлинению волокна 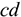 . Ввиду малости угла
. Ввиду малости угла 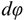 определим дуги
определим дуги 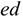 и
и 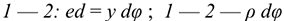 , откуда следует
, откуда следует
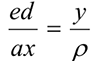
если учесть, что 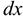 — длина волокна
— длина волокна 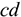 до деформации (см. рис. 114), то станет ясно, что
до деформации (см. рис. 114), то станет ясно, что 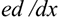 является деформацией волокна
является деформацией волокна 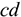 :
:
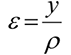
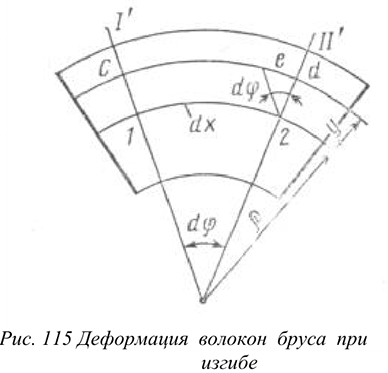
Полученная зависимость показывает что деформация волокна прямо пропорциональна её расстоянию у от нейтрального слоя. Максимальные деформации балка испытывает в точках поперечного сечения максимально удаленных от нейтрального слоя. Для определения напряжений воспользуемся законом Гука
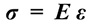
откуда следует после подстановки соотношение
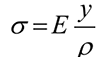
Нормальное напряжение в поперечном сечении при изгибе балки прямо пропорционально расстоянию от нейтральной оси балки. Пользуясь этой зависимостью, можно построить эпюру распределения нормальных напряжений по сечению балки (рис. 116). В нейтральном слое не возникает ни нормальных напряжений, ни деформаций. Линия пересечения нейтрального слоя с поперечным сечением балки называется нейтральной осью.
Определим положение нейтральной оси. Для этого вспомним, что в поперечном сечении сумма всех сил на ось 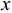 равна нулю, так как при изгибе балки продольных сил нет.
равна нулю, так как при изгибе балки продольных сил нет.
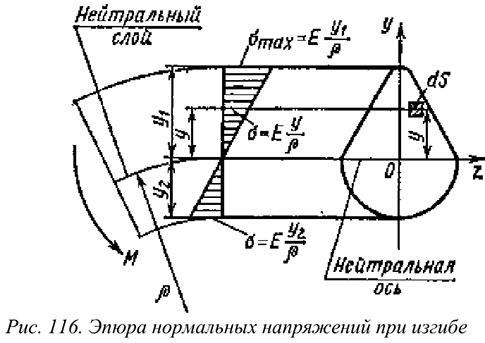
Продольная элементарная сила, действующая на элементарную площадку 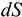 ,
,
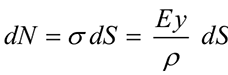
Просуммировав по всей площади, получим
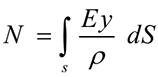
С учетом того, что постоянная величина 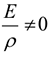 , следует равенство
, следует равенство
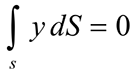
Ранее при рассмотрении геометрических характеристик сечений было показано, что это равенство не что иное, как равенство нулю статического момента площади сечения относительно оси 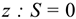 , что свидетельствует о том, что нейтральная ось проходит через центр тяжести сечения 0 (см. рис. 116).
, что свидетельствует о том, что нейтральная ось проходит через центр тяжести сечения 0 (см. рис. 116).
Для количественного определения напряжений необходимо найти радиус кривизны нейтрального слоя деформированной балки 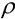 . Запишем очевидное равенство действующего в сечении изгибающего момента
. Запишем очевидное равенство действующего в сечении изгибающего момента 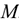 моменту от нормальных сил. Элементарная нормальная сила на расстоянии
моменту от нормальных сил. Элементарная нормальная сила на расстоянии 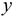 от нейтральной оси, действующая на элементарную площадку
от нейтральной оси, действующая на элементарную площадку 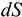 ,
,
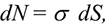
а элементарный момент относительно нейтральной оси
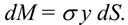
Суммируя элементарные моменты по площади сечения и подставляя выражение
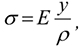
найдем
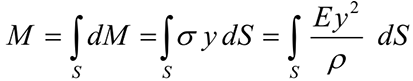
Отсюда определим кривизну изогнутой оси бруса
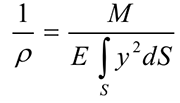
где 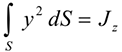 момент инерции поперечного сечения относительно оси
момент инерции поперечного сечения относительно оси 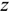 . Подставим выражение кривизны в формулу для
. Подставим выражение кривизны в формулу для 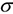 и окончательно после элементарных преобразований получим
и окончательно после элементарных преобразований получим
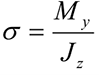
Поскольку нас больше всего интересует максимальное напряжение, то из эпюры изгибающих моментов необходимо найти максимальный изгибающий момент 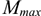 и для поперечного сечения, соответствующего
и для поперечного сечения, соответствующего 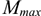 , найти максимальные нормальные напряжения по формуле
, найти максимальные нормальные напряжения по формуле
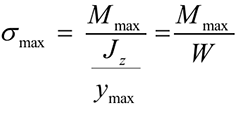
Где 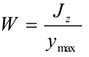 — момент сопротивления изгибу.
— момент сопротивления изгибу.
Формулы для определения момента сопротивления основных сечений изгибу приведены в табл. Эти формулы встречаются в расчетной практике. Числовые значения моментов сопротивления для стандартных профилей проката указаны в соответствующих ГОСТах на прокат.
Момент сопротивления изгибу измеряется в 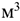 . Если материал балки пластичный, например, сталь, то условие прочности определяется по максимальному напряжению
. Если материал балки пластичный, например, сталь, то условие прочности определяется по максимальному напряжению
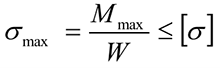
В случае хрупкого материала (чугун) требуется проверка прочности по напряжениям, как растяжения, так и сжатия:
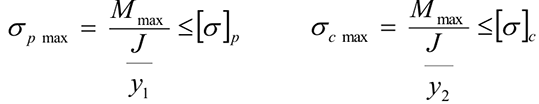
С учетом условий прочности решаются три основные задачи: 1) задача проверки прочности — по заданным нагрузкам и геометрическим размерам поперечного сечения определяют максимальное напряжение в сечении, называемом опасным
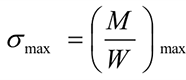
и оно сопоставляется с допускаемым 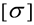 ;
;
2) проектная задача, когда по заданным нагрузкам и допускаемым напряжениям определяют поперечное сечение балки, исходя из момента сопротивления изгибу:
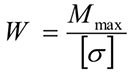
3) задача определения допускаемой нагрузки
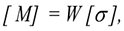
где 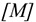 — допускаемая нагрузка, определяемая по опасному сечению балки.
— допускаемая нагрузка, определяемая по опасному сечению балки.
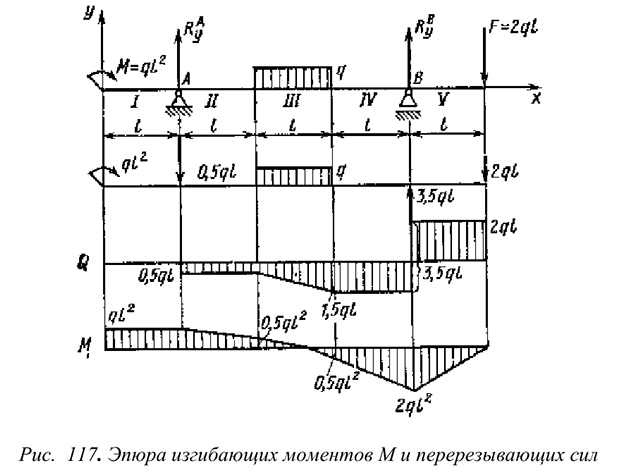
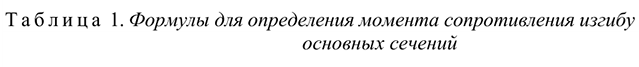
Понятие о касательных напряжениях при изгибе. Линейные и угловые перемещения при изгибе, их определение
Иметь представление о касательных напряжениях при изгибе, об упругой линии балки, о деформациях при изгибе и методах определения линейных и угловых перемещений.
Знать один из методов определения линейных и угловых перемещений. Поперечный изгиб. Внутренние силовые факторы.
Напряжения
Рассмотрим изгиб балки, защемленной справа и нагруженной сосредоточенной силой 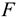 (рис. 33.1).
(рис. 33.1).
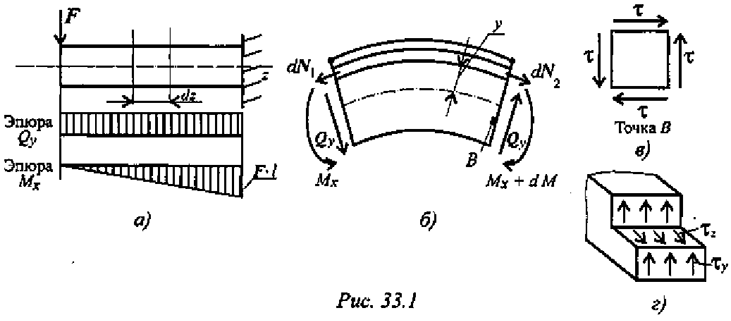
В поперечном сечении возникает изгибающий момент, меняющийся по длине балки, и постоянная поперечная сила  .
.
Рассмотрим участок балки длиной 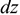 (рис. 33.16). Изгибающий момент, как известно, является равнодействующим элементарных моментов, возникающих в результате действия продольных сил упругости. Связь между нормальными напряжениями в точках поперечного сечения и изгибающим моментом уже рассматривалась:
(рис. 33.16). Изгибающий момент, как известно, является равнодействующим элементарных моментов, возникающих в результате действия продольных сил упругости. Связь между нормальными напряжениями в точках поперечного сечения и изгибающим моментом уже рассматривалась:
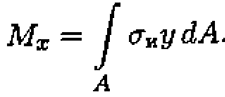
Поперечная сила представляет собой равнодействующую касательных сил упругости, возникающих в поперечных сечениях (рис. 33.1 в), и связана с касательными напряжениями зависимостью
В силу парности касательных
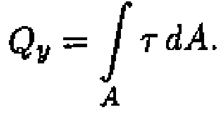
напряжений в продольных сечениях балок, параллельных нейтральному слою, возникают такие же по величине касательные напряжения (рис. 33.1 г).
Появление касательных напряжений в продольных слоях балок подтверждается следующим опытом. Рассмотрим поперечный изгиб двух балок, одна — цельная, другая — составленная из нескольких положенных друг на друга слоев (рис. 33.2). Цельная балка изогнется (рис. 33.2а), брусья второй балки сдвинутся (рис. 33.26). Каждый из брусьев деформируется независимо. В цельной балке сдвигу слоев препятствуют возникающие касательные напряжения.
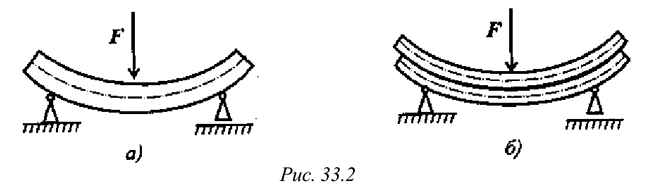
На поверхности касательные напряжения равны нулю. Формула для расчета касательных напряжений для балки квадратного сечения была получена в 1855 году русским инженером Д. И. Журавским,
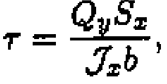
где 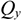 — поперечная сила в сечении;
— поперечная сила в сечении; 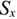 — статический момент отсеченной части относительно оси
— статический момент отсеченной части относительно оси 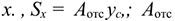 — площадь поперечного сечения отсеченной части (рис. 33.3);
— площадь поперечного сечения отсеченной части (рис. 33.3); 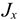 — момент инерции сечения;
— момент инерции сечения; 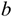 — ширина балки.
— ширина балки.
Наибольшее значение касательного напряжения достигается на нейтральной оси:  — площадь сечения.
— площадь сечения.
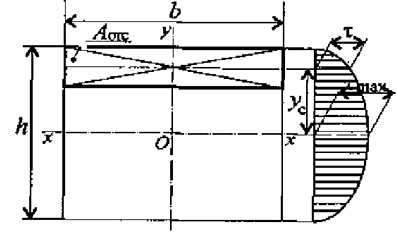
Максимальное
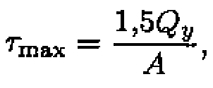
Напряжение при поперечном изгибе в полтора раза больше среднего значения
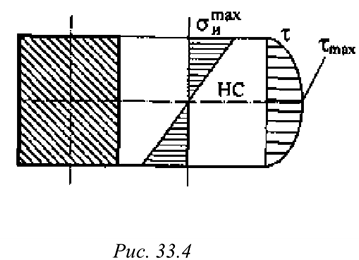
Обнаруживается, что максимальные нормальные напряжения в сечении не совпадают с максимальными касательным (рис 33.4)
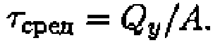
Для длинных балок расчет проводят только по нормальным напряжениям, т. к. касательные здесь незначительны. Для коротких балок, нагруженных значительными поперечными силами вблизи опор, проводят расчет по касательным напряжениям. Однако для тонкостенных профилей (двутавр, швеллер) необходимо проверять £ прочность балки в точках, где полка сочленяется со стенкой. Здесь и нормальные, и касательные напряжения значительны (рис. 33.5). Понятия о линейных и угловых перемещениях при изгибе Под действием поперечных нагрузок продольная ось искривляется (рис. 33.6). Если материал подчиняется закону Гука, после снятия нагрузок брус выпрямляется, поэтому изогнутую ось бруса называют упругой линией. По форме упругой линии балки можно судить о перемещениях при изгибе.
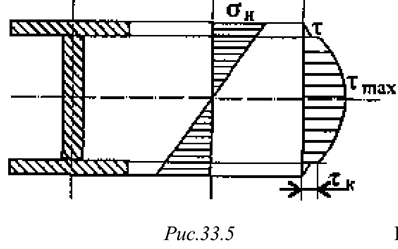
При прямом поперечном изгибе бруса его ось, искривляясь, остается в силовой плоскости. В результате деформации бруса каждое из его поперечных сечений получает вертикальное и горизонтальное перемещение, а само сечение поворачивается на некоторый угол 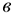 .
.
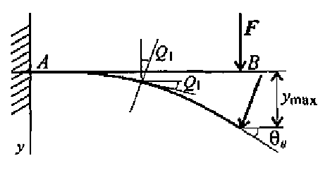
Деформации должны иметь упругий характер, они достаточно малы. В этом случае горизонтальные перемещения сечений ничтожно малы и не учитываются. Рассматривают вертикальные перемещения центра тяжести сечения, называемые прогибами 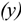 . Максимальные прогибы обозначают
. Максимальные прогибы обозначают 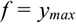 . Для обеспечения нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость. Условие жесткости выражается неравенством где
. Для обеспечения нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость. Условие жесткости выражается неравенством где 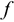 — максимальный расчетный прогиб балки;
— максимальный расчетный прогиб балки; 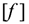 — допускаемый прогиб. Иногда проверяется угол поворота сечения
— допускаемый прогиб. Иногда проверяется угол поворота сечения 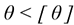 . Допускаемый прогиб невелик: от 1/200 до 1/1000 пролета балки; допускаемый угол поворота
. Допускаемый прогиб невелик: от 1/200 до 1/1000 пролета балки; допускаемый угол поворота 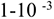 рад.
рад.
Существует несколько методов определения перемещений сечений при изгибе. Один из них основан на дифференцировании уравнения упругой линии, более рациональный способ — использование интегралов Мора. Метод Мора — универсальный способ определения линейных и угловых перемещений в любых системах.
Для облегчения расчетов на жесткость можно использовать формулы прогибов и углов поворота сечений балок для простейших случаев нагружений. Наиболее распространенные случаи нагружения и расчетные формулы приведены в таблице.
При решении используем принцип независимости действия сил. Заданный случай нагружения делится на составляющие, для которых прогибы рассчитываются по известным табличным формулам, результаты расчетов суммируются.
Ограничение угла поворота вводится для обеспечения нормальной работы подшипников скольжения и роликовых подшипников.
В этом случае проверяется дополнительное условие жесткости:
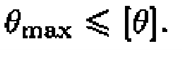
Сочетание основных деформаций. Гипотезы прочности
Иметь представление о напряженном состоянии в точке упругого тела, о теории предельных напряженных состояний, об эквивалентном напряженном состоянии, о гипотезах прочности.
Знать формулы для эквивалентных напряжений по гипотезам наибольших касательных напряжений и энергии формоизменения.
Напряженное состояние в точке
Напряженное состояние в точке характеризуется нормальными и касательными напряжениями, возникающими на всех площадках (сечениях), проходящих через данную точку. Обычно достаточно определить напряжения на трех взаимно перпендикулярных площадках, проходящих через рассматриваемую точку. Точку принято изображать в виде маленького элемента в форме параллелепипеда (рис. 34.1).
Положения теории напряженного состояния:
- Напряженное состояние в данной точке полностью определено, если известны напряжения по любым трем взаимно перпендикулярным площадкам.
- Среди множества площадок, которые можно провести через данную точку, есть три такие взаимно перпендикулярные площадки, на которых отсутствуют касательные напряжения, эти площадки называются главными, а нормальные напряжения, возникающие на них, называются главными напряжениями:
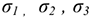 (рис. 34.1).
(рис. 34.1).
Одно из этих напряжений — максимально, одно — минимально. Максимальное обозначают  , минимальное —
, минимальное —  .
.
Классификация видов напряженного состояния производится по главным напряжениям:
—если все три главных напряжения не равны нулю, то напряженное состояние называют объемным (трехосным) (рис. 34.1 а);
—если одно из главных напряжений равно нулю, напряженное состояние называют плоским (двухосным) (рис. 34.16);
—если два из главных напряжений  ) противоположны по знаку, напряженное состояние называют упрощенным плоским состоянием; — если лишь одно из главных напряжений не равно нулю, напряженное состояние линейное (рис. 34.1 в).
) противоположны по знаку, напряженное состояние называют упрощенным плоским состоянием; — если лишь одно из главных напряжений не равно нулю, напряженное состояние линейное (рис. 34.1 в).
Понятие о сложном деформированном состоянии
Совокупность деформаций, возникающих по различным направлениям и в различных плоскостях, проходящих через точку, определяют деформированное состояние в этой точке.
Сложное деформированное состояние возникает, если деталь одновременно подвергается нескольким простейшим нагружениям.
Такие состояния возникают в заклепочных соединениях (срез и смятие), в болтовых соединениях (растяжение и скручивание), при поперечном изгибе бруса (изгиб и сдвиг).
Часто одним из нагружений (незначительным) пренебрегают.
Например, длинные балки рассчитывают только на изгиб.
В ряде случаев нормальные и касательные напряжения, возникающие в детали, имеют одинаковый порядок и ими нельзя пренебрегать. Тогда расчет проводят при сложном деформированном состоянии.
Сложность расчета заключается в отсутствии экспериментальных данных о предельных напряжениях, т.к. провести испытания из-за множества вариантов нагружения практически невозможно.
Для упрощения расчетов в этом случае применяют теории прочности. Смысл теорий заключается в замене реального сложного деформированного состояния равноопасным простым.
Опасное состояние может быть вызвано различными факторами: нормальные напряжения могут достигнуть предела текучести или предела прочности, касательные напряжения могут достигнуть опасного значения или накопленная энергия деформирования может стать слишком большой и вызвать разрушение.
Универсального критерия, позволяющего рассчитать предельное состояние для любого материала, нет. Разработано несколько различных гипотез предельных состояний, при расчетах используют наиболее подходящую гипотезу. Расчеты по гипотезам прочности позволяют избегать дорогостоящих испытаний конструкции.
В настоящее время для расчета валов при совместном действии изгиба и кручения используют только третью и пятую теории прочности.
Сравнение разнотипных состояний производится с помощью эквивалентного (простого) напряженного состояния. Обычно сложное напряженное состояние заменяют простым растяжением (рис. 34.2).
Расчетное напряжение, соответствующее выбранному одноосному растяжению, называют эквивалентным напряжением (рис. 34.26).
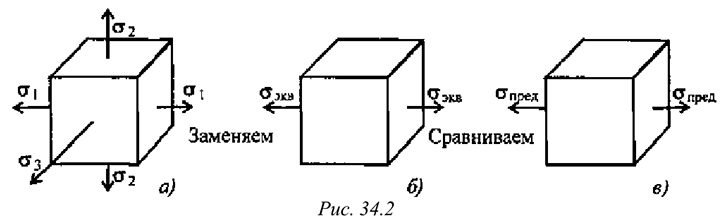
Полученное расчетным путем эквивалентное напряжение для точки сравнивают с предельным (рис. 34.2в).
Напряженное состояние в точке равноопасно эквивалентному напряженному состоянию. Условие прочности получим, сопоставив эквивалентное напряжение с предельным, полученным экспериментально для выбранного материала:, где 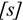 — допускаемый запас прочности
— допускаемый запас прочности
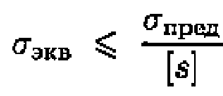
Как известно, предельным напряжением для пластичных материалов является предел текучести 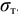 , а для хрупкого — предел прочности
, а для хрупкого — предел прочности 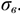 . Предельное напряженное состояние у пластичных материалов наступает в результате пластических деформаций, а у хрупких — в результате разрушения.
. Предельное напряженное состояние у пластичных материалов наступает в результате пластических деформаций, а у хрупких — в результате разрушения.
Для пластичных материалов расчет может выполняться по гипотезе максимальных касательных напряжений: два напряженных состояния равноопасны, если максимальные касательные напряжения у них одинаковы (третья теория прочности).
Расчет можно проводить и по теории потенциальной энергии формоизменения: два напряженных состояния равноопасны, если энергия формоизменения у них одинакова (пятая теорема прочности).
Для хрупких и хрупко-пластичных материалов применяют теорию прочности Мора.
Расчет эквивалентного напряжения для точки по теории максимальных касательных напряжений выполняется по формуле
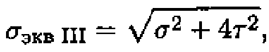
а по теории энергии формоизменения по формуле
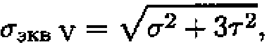
где 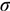 — действующее в точке нормальное напряжение;
— действующее в точке нормальное напряжение; 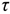 — действующее в точке касательное напряжение.
— действующее в точке касательное напряжение.
Расчет круглого бруса на изгиб с кручением
В случае расчета круглого бруса при действии изгиба и кручения (рис. 34.3) необходимо учитывать нормальные и касательные напряжения, т. к. максимальные значения напряжений в обоих случаях возникают на поверхности. Расчет следует вести по теории прочности, заменяя сложное напряженное состояние равноопасным простым.
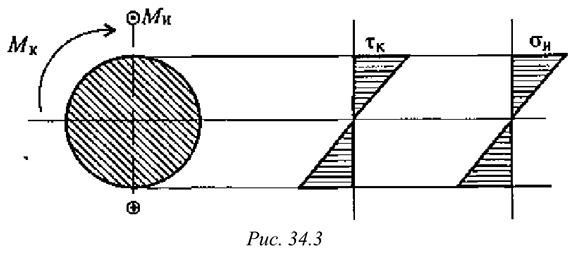
Максимальное напряжение кручения в сечении
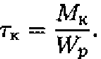
Максимальное напряжение изгиба в сечении
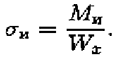
По одной из теорий прочности в зависимости от материала бруса рассчитывают эквивалентное напряжение для опасного сечения и проверяют брус на прочность, используя допускаемое напряжение изгиба для материала бруса. Для круглого бруса моменты сопротивления сечения следующие:
при кручении
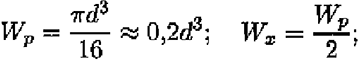
при изгибе
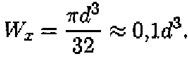
При расчете по третьей теории прочности, теории максимальных касательных напряжений, эквивалентное напряжение рассчитывается по формуле
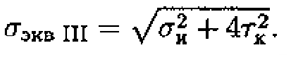
Теория применима для пластичных материалов. При расчете по теории энергии формоизменения эквивалентное напряжение рассчитывается по формуле
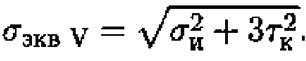
Теория применима для пластичных и хрупких материалов. Эквивалентное напряжение при расчете по теории максимальных касательных напряжений:
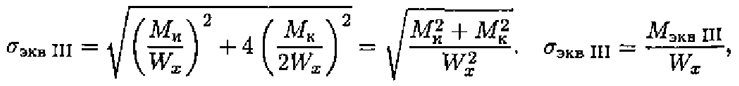
где
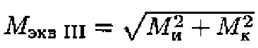
эквивалентный момент.
Условие прочности
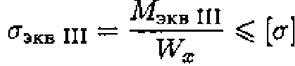
Эквивалентное напряжение при расчете по теории энергии формоизменения:
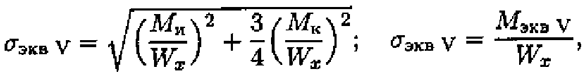
где
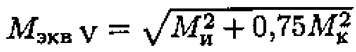
эквивалентный момент.
Условие прочности
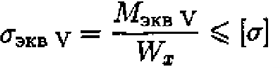
Устойчивость сжатых стержней. Основные положения
Иметь представление об устойчивых и неустойчивых формах равновесия, критической силе и коэффициенте запаса устойчивости, о критическом напряжении, гибкости стержня и предельной гибкости.
Знать условие устойчивости сжатых стержней, формулу Эйлера и эмпирические формулы для расчета критической силы и критического напряжения.
Понятие об устойчивом и неустойчивом равновесии
Относительно короткие и массивные стержни рассчитывают на сжатие, т.к. они выходят из строя в результате разрушения или остаточных деформаций. Длинные стержни небольшого поперечного сечения под действием осевых сжимающих сил изгибаются и теряют равновесие. Такие стержни работают на изгиб и сжатие.
Равновесие считают устойчивым, если за счет сил упругости после снятия внешней отклоняющей силы стержень восстановит первоначальную форму (рис. 36.1). Если упругое тело после отклонения от равновесного положения не возвращается к исходному состоянию, то говорят, что произошла потеря устойчивости, а равновесие было неустойчивым.
Потерю устойчивости под действием центрально приложенной продольной сжимающей силы называют продольным изгибом.
На устойчивость равновесия влияет величина сжимающей силы.
Наибольшее значение сжимающей силы, при которой прямолинейная форма стержня сохраняет устойчивость, называют критической силой. Даже при небольшом превышении критического значения силы стержень недопустимо деформируется и разрушается.
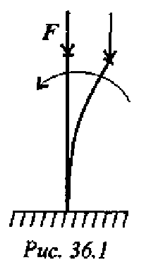
Расчет на устойчивость
Расчет на устойчивость заключается в определении допускаемой сжимающей силы и в сравнении с ней силы действующей:
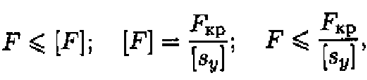
где 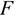 — действующая сжимающая сила;
— действующая сжимающая сила;
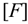 — допускаемая сжимающая сила, обеспечивает некоторый запас устойчивости;
— допускаемая сжимающая сила, обеспечивает некоторый запас устойчивости;
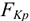 — критическая сила;
— критическая сила;
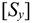 — допускаемый коэффициент запаса устойчивости.
— допускаемый коэффициент запаса устойчивости.
Обычно для сталей 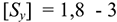 ; для чугуна
; для чугуна 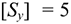 ; для дерева
; для дерева 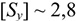 .
.
Способы определения критической силы
Расчет по формуле Эйлера
Задачу определения критической силы математически решил Л. Эйлер в 1744 г.
Для шарнирно закрепленного с обеих сторон стержня (рис. 36.2) формула Эйлера имеет вид
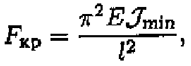
где 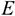 — модуль упругости;
— модуль упругости;
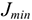 — минимальный осевой момент инерции стержня;
— минимальный осевой момент инерции стержня;
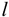 — длина стержня.
— длина стержня.
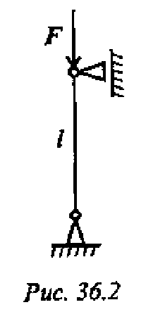
Потеря устойчивости происходит в плоскости наименьшей жесткости, поэтому в формулу входит минимальный из осевых моментов инерции сечения (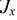 или
или 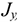 ).
).
Формулу распространили на другие формы закрепления стержней, рассмотрев форму потери устойчивости в каждом случае.
Длина стержня заменяется ее приведенным значением, учитывающим форму потери устойчивости в каждом случае: 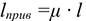 где
где 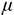 — коэффициент приведения длины, зависящий от способа закрепления стержня (рис. 36.3). Формула для расчета критической силы для всех случаев
— коэффициент приведения длины, зависящий от способа закрепления стержня (рис. 36.3). Формула для расчета критической силы для всех случаев
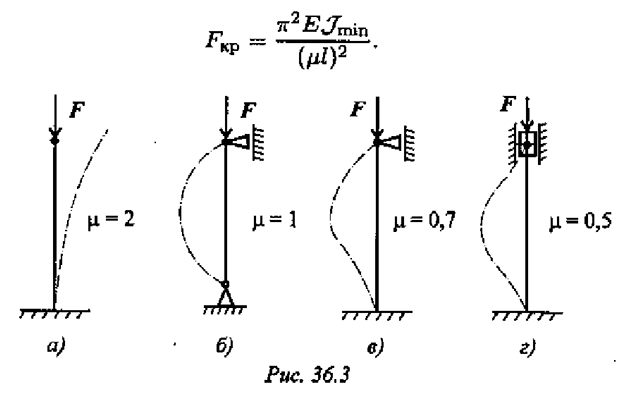
Критические напряжения.
Критическое напряжение — напряжение сжатия, соответствующее критической силе.
Напряжение от сжимающей силы определяется по формуле
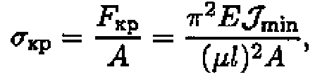
где 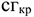 — напряжение сжатия, при котором стержень еще устойчив. Корень квадратный из отношения минимального момента инерции сечения к площади поперечного сечения принято называть минимальным радиусом инерции
— напряжение сжатия, при котором стержень еще устойчив. Корень квадратный из отношения минимального момента инерции сечения к площади поперечного сечения принято называть минимальным радиусом инерции 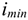 :
:
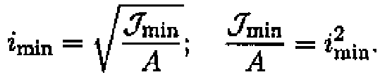
Тогда формула для расчета критического напряжения перепишется в виде
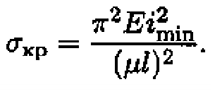
Отношение 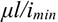 носит название гибкости стержня
носит название гибкости стержня 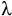 . Гибкость стержня — величина безразмерная, чем больше гибкость, тем меньше напряжен
. Гибкость стержня — величина безразмерная, чем больше гибкость, тем меньше напряжен
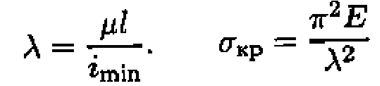
Заметим, что гибкость не зависит от материала, а определяется только геометрией стержня.
Пределы применимости формулы Эйлера
Формула Эйлера выполняется только в пределах упругих деформаций.
Таким образом, критическое напряжение должно быть меньше предела упругости материала.
Предел упругости при расчетах можно заменять пределом пропорциональности. Таким образом,
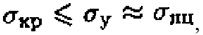
где 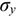 — предел упругости;
— предел упругости; 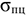 — предел пропорциональности материала;
— предел пропорциональности материала;
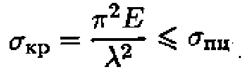
Откуда гибкость стержня:
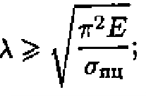
Предельная гибкость:
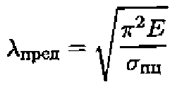
В случае, если 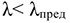 в материале стержня возникают остаточные деформации. Поскольку в реальных конструкциях могут возникать пластические деформации, не приводящие к потере работоспособности, созданы эмпирические формулы для расчетов в этих случаях.
в материале стержня возникают остаточные деформации. Поскольку в реальных конструкциях могут возникать пластические деформации, не приводящие к потере работоспособности, созданы эмпирические формулы для расчетов в этих случаях.

