Свойства, выражаемые неравенствами

Оглавление:

Свойства, выражаемые неравенствами

Свойства, выражаемые неравенствами. И все же мы Мы приняли во внимание характеристики Интеграла, которые выражаются в Равенствах. Теперь обратимся к тому, что представляет собой неравенство. 5°.Если интегрируемая функция f (x) в интервале[a, b \не отрицательна、 б ^ /(х) УГ ^:0. Но… Доказательства очевидны. Простой результат этого(и от 4°) является 6°.Если обе функции f(x)и Chi(x) интегрируемы в интервале[a, b], и всегда f (x)* <$(x)、 б \ /(х) топор ^ \ е (х) топор Но、 в предположении, что a ^ b. Просто примените предыдущее свойство к разнице e (x)-/(x). 7°.Пусть функция f (x) интегрируется на интервале[a, b \и a> b. функция| /(x) / интегрируется в этом интервале и является неравенством /(*)! ** ■ Но.

Доказанному соотношению можно придать более удобную форму равенства, но оно освобождается от ограничения a Людмила Фирмаль

Во-первых, проверьте существование интеграла от| / (^)|.Если взять любые 2 точки n ’и x «в интервале[x1P ^ / + 1], то| n°8] | | / (*») Я-| /(n011 \ /(х») -/(.Х’). Так что вы подразумеваете под w. Функция вибрация [/(l;) / интервал[x {,; c (W.], вибрация[N ° 73]по определению,^ *>;» о 2 ВХ,^ *） » Тенденция суммы правой стороны к нулю одинакова для суммы левой стороны. Сами неравенства легко получить непосредственно из интегральной суммы. 21/6) и Д * * * > Двенадцать /＆） И тогда мы переходим к пределу. 8°. если F(х) [а, б м * ^ /(х)* ^ м、 И затем… б м(Б-а)$ $ $ /(・*) т * ^ м(Б-а). Но… Свойство 6°может быть применено к функциям m, f(x), но проще использовать очевидные неравенства напрямую м 2 Д * С /&)Д * р ^ 2 ^ 1 /

А потом идти до предела. ) начиная с A b, все a ^> 0. 9°.Теорема о среднем значении. пусть f (x) интегрируемо с[a, b] (a0 b), и пусть m> f (x)> M на протяжении этого интервала. И затем… б л /(х) ЛК = р(б-а）、 Вот м ^ м Доказательство. для Ab, по свойству 8°、 б «»Р г:^ г. Похлопывание О ыы$ /（）** = 1 *。 Получите равенство, которое вам нужно. Но… в случае a> b он выполняет те же аргументы, переставляет ограничения и достигает предыдущего выражения. Только что доказанное равенство принимает особенно простую форму, когда функция/(x) имеет вид contiguous.

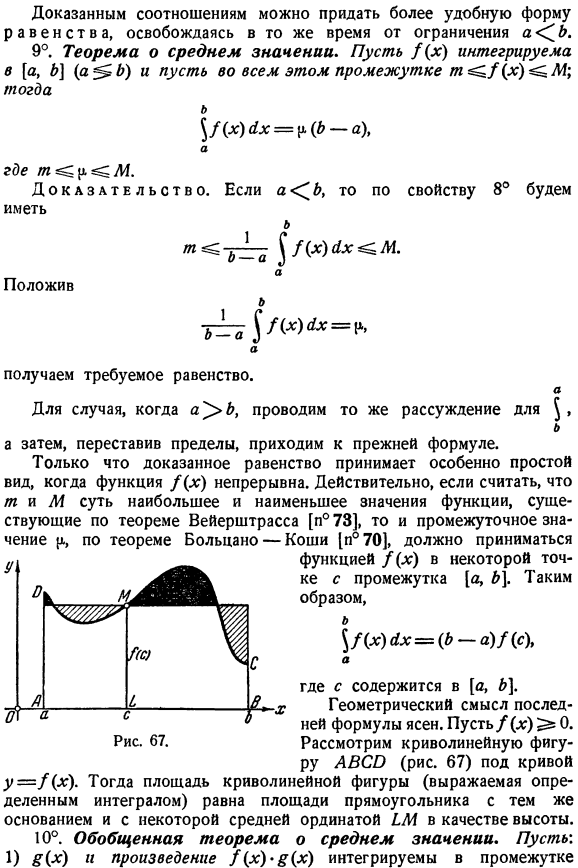
Факт, если мы предположим, что m и M являются максимумом и минимумом функции, представленной теоремой Вейерштрасса[N°73], то мы должны принять промежуточное значение I . Из-за теоремы Больцано-Коши[n°70]. Функция f (x) в некоторой точке из интервала[a, b].Подобный этому \ /(х) DX =(Б-а)/(с）、 c включен в[a, b]. Геометрический смысл последнего выражения ясен. допустим, f (x)> 0.Рассмотрим кривую диаграммы АБКО под кривой (рис. 67 у = F(х).Тогда площадь криволинейной фигуры (представленной неким интегралом) будет равна площади прямоугольника со средней ординатой LM в качестве одинакового основания и высоты. 10°.

Теорема обобщенного среднего значения. O 8(x) 11, произведение f (x) * e (x) есть интервал[a, b \ 2) m ^./ (X) предположим, что он интегрируется по<M. 3)$(x) через интервал не изменяет знак. ^(х)^ 0 [#(х)^ 0].И затем… б \ 1(х) 8 (х) топор = г.\ Е (х) топор、 Но、 Вот, м ^ ^ ^м. Доказательство. Во-первых, пусть^(x)^ = 0 и a ^ b. тогда мы имеем U(Х)<ф (х)§(х) я (х). Из этого неравенства, основанного на характеристиках 6°и 3°, получаем: М \ 8 (х) топор\^}: (х) 8 (х) топор \ ^ 8 м (х) Ах. ля. Рассмотрим предположение о функции # ( * ) через каждые 5° б \ е(х) Но… Если этот Интеграл равен нулю, то из предыдущего неравенства, в то же время Но… И описание теоремы становится понятным. Если Интеграл больше нуля, то разделите все части полученного выше двойного неравенства на、 б \ / (X) 2 (X) AX.

Сохраняются ограничения a и b, между которыми изменяется переменная. Людмила Фирмаль

Но… =северный\ Е(Х) Х Но… И тогда вы достигнете желаемого результата. Фактически, ограничение, что a ^ b не требуется, является: Изменение положения предела или знака$(x)не нарушает равенства. если f (x) непрерывна, то эту формулу можно записать следующим образом: б л /(х) 8 (х) топор = F © 5 8 (х) ЛК、 Но、 c включен в[a, b]. Замечания. Интегральная переменная всегда обозначается буквой X. Но, конечно, если ничего не изменилось、 вместо x я использовал другие символы. б Подынтегральная Функция Λ.Символ$ / (x) dx означает точно то же самое Но… Б, б. число, например u или/ / ^® y. By это очевидное замечание、 Но、 Используй его сейчас.

Интеграл по ориентированному промежутку.	Определенный интеграл как функция верхнего предела.
Свойства, выражаемые равенствами.	Вычисление с помощью интегральных сумм.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.