Свойства функций, имеющих предел
Свойства будут сформулированы для функций, имеющих предел в точке, но они очевидным образом могут быть перенесены па случай предела функции на бесконечности.
- Если функция имеет предел в точке, то он единственен.
- Функция, имеющая предел в точке, ограничена в некоторой проколотой окрестности этой точки.
- Если
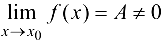, то найдется проколотая окрестность точки 
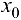, в которой функция 
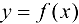имеет знак, совпадающий со знаком предела А. - Если функции
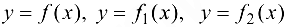в некоторой проколотой окрестности точки 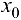связаны соотношением 
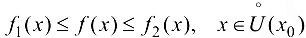, причем 
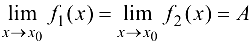то существует 
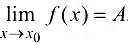. - Если
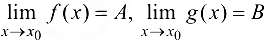, то:
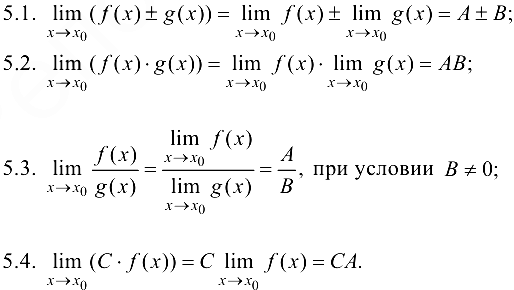
Доказательство этих свойств вытекает из аналогичных свойств пределов числовых последовательностей, если воспользоваться определением предела функции в точке по Гейне.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
