Свойства действительных чисел. Основные подмножества множества действительных чисел
На этой странице мы перечислим основные свойства множества R действительных чисел. которыми оно полностью определяется. Многие из этих свойств известны из курса элементарной математики. При изложении мы будем также считать известными простейшие понятия теории множеств и принятые там обозначения.
Сформулируем сначала свойства, касающиеся операций сложения и умножения действительных чисел.
1) Коммутативность: 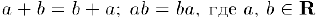 .
.
2) Ассоциативность — 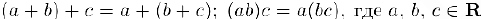
3) Существуют числа 0 (нуль) и 1 (единица) такие, что 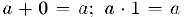 для любого
для любого 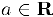 .
.
4) Для любого 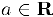 существует противоположное ему число —
существует противоположное ему число — 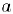 , для которого
, для которого 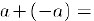 0. Если, кроме того,
0. Если, кроме того, 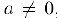 , то найдется также число
, то найдется также число 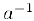 (обратное данному) такое, что
(обратное данному) такое, что 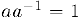 .
.
Число 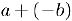 называется разностью действительных чисел
называется разностью действительных чисел 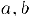 и обозначается через
и обозначается через  . Аналогично, частным от деления чисел
. Аналогично, частным от деления чисел 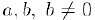 называется число
называется число 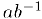 которое обозначается через
которое обозначается через 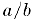 .
.
5) Дистрибутивность: 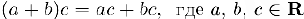 .
.
Теперь остановимся на свойствах упорядоченности множества действительных чисел. Упорядоченность означает, что любые два действительных числа 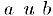 сравнимы, т. е. для них выполняется одно их трех соотношений:
сравнимы, т. е. для них выполняется одно их трех соотношений: 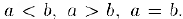 . Число
. Число 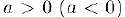 называется положительным (отрицательным).
называется положительным (отрицательным).
6) Транзитивность: из неравенств 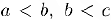 для действительных чисел
для действительных чисел 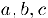 следует неравенство
следует неравенство 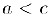 .
.
7) Если 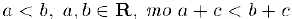 для любого числа с.
для любого числа с.
8) Для любых положительных чисел 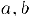 произведение ab также положительно.
произведение ab также положительно.
Отсюда и из свойств 5) и 7), в частности, следует, что. если 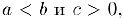 , то
, то 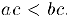 .
.
Укажем еще одно важное свойство множества действительных чисел.
9) Полнота (непрерывность). Пусть А и В — произвольные числовые множества. Если для любых чисел 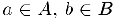 выполняется неравенство
выполняется неравенство 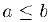 , то существует число-разделитель с такое, что
, то существует число-разделитель с такое, что 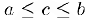 для всех
для всех 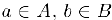 .
.
Например, если множества А и В составляют рациональные числа, квадраты которых меньше и больше 2, соответственно, то разделителем здесь служит число 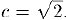 .
.
Определим теперь основные подмножества множества действительных чисел.
а) Множество натуральных чисел N составляют числа
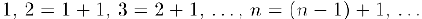
Такое определение множества натуральных чисел является основой метода математической индукции: если имеется утверждение 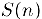 , зависящее от произвольного натурального номера
, зависящее от произвольного натурального номера 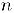 , то для его доказательства необходимо проверить его при
, то для его доказательства необходимо проверить его при 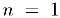 , а затем, предположив. что оно верно для всех номеров, не превосходящих
, а затем, предположив. что оно верно для всех номеров, не превосходящих 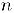 , доказать справедливость утверждения
, доказать справедливость утверждения 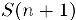 .
.
В качестве примера применения метода математической индукции приведем доказательство неравенства Бернулли
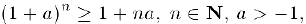
которое мы будем использовать в дальнейшем.
Доказательство. Очевидно, при 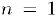 неравенство справедливо. Предположим, что оно верно для номера
неравенство справедливо. Предположим, что оно верно для номера 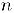 . Умножив обе его части на положительное число
. Умножив обе его части на положительное число 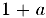 , получим
, получим
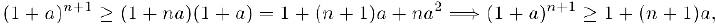
что и требовалось доказать.
b) Множество целых чисел: 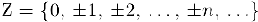 .
.
c) Множество рациональных чисел: 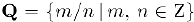 .
.
d) Множество иррациональных чисел: 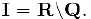
Отметим еще некоторые подмножества множества действительных чисел, которые мы часто будем использовать в дальнейшем. Пусть 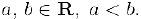 . Тогда:
. Тогда:
e) интервал числовой оси: 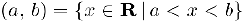 :
:
f) отрезок числовой оси: 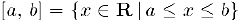 :
:
g) полуинтервалы числовой оси: 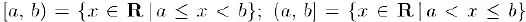 . Множества е) — g) называются промежутками числовой оси.
. Множества е) — g) называются промежутками числовой оси.
Неограниченный в какую-нибудь сторону промежуток числовой оси называется полуосью или бесконечным промежутком.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
| Числовые множества |
| Предел последовательности |
| Векторная функция действительного аргумента: определение, теорема и доказательство |
| Комплексные числа и операции над ними. Разложение полинома на множители |

